Определение положения центра тяжести сложной фигуры
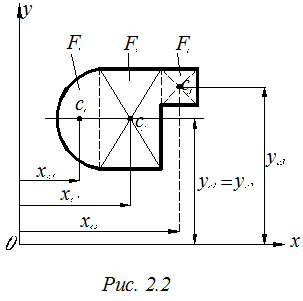 |
Для определения координат центра тяжести сложной фигуры выбирается произвольная система координат хоу (рис. 2.2). Сложное сечение разбивается на простые фигуры, для которых известно значение величины площади Fi и положение координат центра тяжести Xci и Yci. i =1, 2, 3…n. Координаты центра тяжести всей фигуры определяются по формулам (2.1 и 2.2).
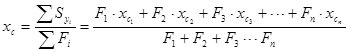 (2.1)
(2.1)
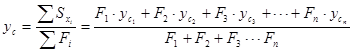 (2.2)
(2.2)
Зависимость между моментами инерции относительно параллельных осей
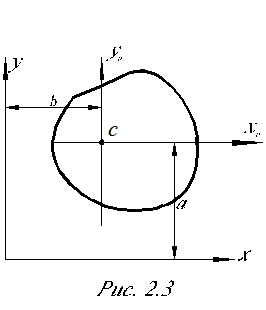 Для произвольной фигуры площадью F известны моменты инерции относительно центральных осей х0 и у0:
Для произвольной фигуры площадью F известны моменты инерции относительно центральных осей х0 и у0: 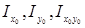 , рис. 2.3.
, рис. 2.3.
Соответствующие осевые и центробежный момент инерции относительно новых осей х и у, которые параллельны осям х0, у0 можно определить с помощью формул (2.3, 2.4, 2.5):
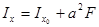 (2.3)
(2.3)
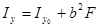 (2.4)
(2.4)
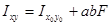 (2.5)
(2.5)
Переносить можно только центральные оси инерции.
Зависимость между моментами инерции при повороте осей координат
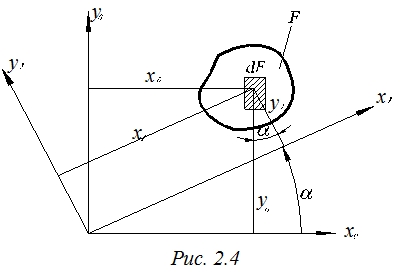 Известны моменты инерции относительно осей х0 и у0 - Ix0, Iy0, Ix0,y0 (рис.2.4).
Известны моменты инерции относительно осей х0 и у0 - Ix0, Iy0, Ix0,y0 (рис.2.4).
Осевые и центробежный момент инерции относительно новых осей х1 и у1, повернутых относительно исходной системы координат на угол α, можно определить по формулам (2.6, 2.7, 2.8).
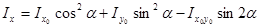 (2.6)
(2.6)
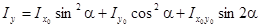 (2.7)
(2.7)
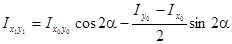 (2.8)
(2.8)
Центральные оси инерции – оси, проходящие через центр тяжести сечения.
Главные оси инерции – оси, относительно которых центробежный момент инерции 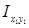 = 0.
= 0.
Главные центральные оси инерции – главные оси, проходящие через центр тяжести сечения.
Для моментов инерции относительно осей х, у и х1 и у1 справедливо соотношение
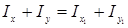 (2.9)
(2.9)
Главные моменты инерции
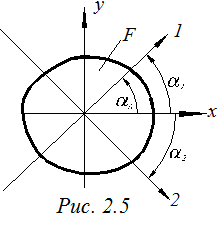
Моменты инерции относительно осей 1 и 2, для которых I1,2=0, называются главными и определяются по формуле (2.10). Для I1 перед корнем берется знак (+), для I2 (–) (рис. 2.5).
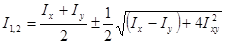 (2.10)
(2.10)
Моменты инерции относительно главных осей обладают свойством экстремальности:
I1 = Imax I2 = Imin. (2.11)
Положение главных осей инерции
Положение главных осей инерции (рис. 2.5) можно определить по формуле (2.12) или (2.13).
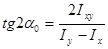 (2.12)
(2.12)
Положение главных осей инерции 1 и 2 можно найти и так:
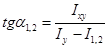 (2.13)
(2.13)
угол α1 соответствует оси 1, угол α2 – оси 2. Отсчет углов α1 и α2 ведется от положительного направления оси х.
2.7. Моменты сопротивления Wx, Wy
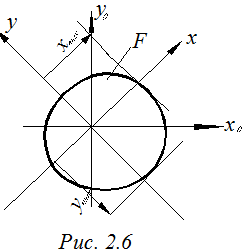
Осевые моменты сопротивления Wx, Wy используются для подбора поперечных сечений балок при изгибе (рис. 2.6):
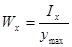 (см3)
(см3) 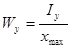 (см3) (2.14)
(см3) (2.14)
уmax и хmax – соответственно расстояния от осей х и у до наиболее удаленных точек сечения.
Радиусы инерции сечения ix и iy находятся из выражения (2.15):
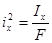 (см2)
(см2) 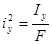 (см2) (2.15)
(см2) (2.15)
Растяжение (сжатие)
Напряжения и деформации
Растяжение (сжатие) – деформация, при которой все равнодействующие всех сил лежат на одной оси, совпадающей с продольной осью стержня (рис.3.1). Внутреннее усилие Nz определяется с использованием метода сечений.
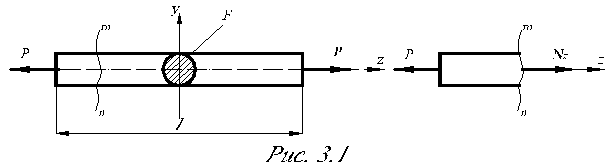 |
ΣFz = 0: Nz = P (3.1)
NZ – продольное усилие.
Нормальное напряжение при растяжении определяется:
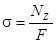 (3.2)
(3.2)
Условие прочности при растяжении:
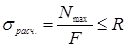 – (3.3)
– (3.3)
Здесь R – расчетное сопротивление материала 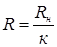 ,
,
где Rн – нормативное сопротивление материала, устанавливаемое нормами проектирования,
к – коэффициент безопасности по материалу.
Абсолютное удлинение элемента 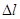 может быть определено как (3.4) (рис. 3.2):
может быть определено как (3.4) (рис. 3.2):
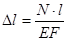 (3.4)
(3.4)
EF – жесткость стержня при растяжении.
Е – модуль упругости стали при растяжении Е = 2·105МПа.
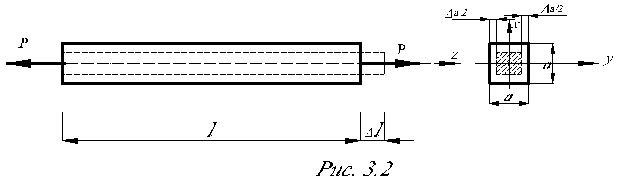
При растяжении стержень в продольном направлении удлиняется на величину ∆l, а в поперечном направлении сужается на величину ∆а (рис.3.2):
∆l – абсолютная продольная деформация,
∆а – абсолютная поперечная деформация.
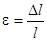 – относительная продольная деформация,
– относительная продольная деформация,
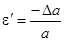 – относительная поперечная деформация.
– относительная поперечная деформация.
Отношение: 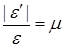 – коэффициент Пуассона
– коэффициент Пуассона
0 ≤ µ ≤ 0,5 (3.5)
Упругие постоянные Е и µ определяются по справочным данным в зависимости от материала элемента (см. часть 2).
