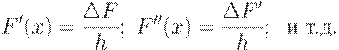ПЗ 6. Метод с использованием производной целевой функции. Метод Фибоначчи

Одним из методов однопараметрической оптимизации является метод Фибоначчи.

Предположим, что нужно определить минимум как можно точнее, т.е. с наименьшим возможным интервалом неопределенности, но при этом можно выполнить только n вычислений функции. Как следует выбрать n точек, в которых вычисляется функция? С первого взгляда кажется ясным, что не следует искать решение для всех точек, получаемых в результате эксперимента. Напротив, надо попытаться сделать так, чтобы значения функции, полученные в предыдущих экспериментах, определяли положение последующих точек. Действительно, зная значения функции, мы тем самым имеем информацию о самой функции и положении ее минимума и используем эту информацию в дальнейшем поиске.

Предположим, что имеется интервал неопределенности (x₁,x₃) и известно значение функции f(x₂) внутри этого интервала (см. рис. 3). Если можно вычислить функцию всего один раз в точке х₄, то где следует поместить точку х₄, для того чтобы получить наименьший возможный интервал неопределенности?

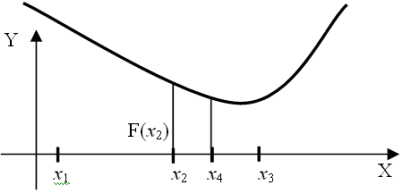
Рис.3.

Положим х₂–х₁=L и х₃–х₂=R, причем L > R, как показано на рис. 3, и эти значения будут фиксированы, если известны x₁, x₂ и х₃. Если х₄ находится в интервале (х₁; х₂), то:

1. если f(x₄) < f(x₂), то новым интервалом неопределенности будет (x₁,x₂) длиной х₂–х₁=L ;

2. если f(х₄)>f(x₂), то новым интервалом неопределенности будет (х₄,х₃) длиной х₃–х₄.

Поскольку не известно, какая из этих ситуаций будет иметь место, выберем х₄ таким образом, чтобы минимизировать наибольшую из длин х₃-х₄ и х₂-х₁. Достигнуть этого можно, сделав длины х₃ – х₄ и х₂ – х₁ равными т.е. поместив х₄ внутри интервала симметрично относительно точки х₂, уже лежащей внутри интервала. Любое другое положение точки х₄ может привести к тому, что полученный интервал будет больше L. Помещая х₄ симметрично относительно х₂, мы ничем не рискуем в любом случае. Если окажется, что можно выполнить еще одно вычисление функции, то следует применить описанную процедуру к интервалу (х₁, х₂), в котором уже есть значение функции, вычисленное в точке х₄, или к интервалу (х₄,х₃), в котором уже есть значение функции, вычисленное в точке х₂.

Следовательно, стратегия ясна с самого начала. Нужно поместить следующую точку внутри интервала неопределенности симметрично относительно уже находящейся там точке. Парадоксально, но, чтобы понять, как следует начинать вычисления, необходимо разобраться в том, как его следует кончать.

На n -м вычислении n -ю точку следует поместить симметрично по отношению к (n — 1) -й точке. Положение этой последней точки в принципе зависит от нас. Для того чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка х будет совпадать с точкой х_n-1. Однако при этом мы не получаем никакой новой информации. Обычно точки х_n-1 и х_n отстоят друг от друга на достаточном расстоянии, чтобы определить, в какой половине, левой или правой, находится интервал неопределенности. Они помещаются на расстоянии е/2 по обе стороны от середины отрезка L_n-1 ; можно самим задать величину е или выбрать эту величину равной минимально возможному расстоянию между двумя точками.

Интервал неопределенности будет иметь длину L_n, следовательно, L_n-1 = 2L_n - е (рис.4), нижняя часть). На предыдущем этапе точки х_n-1 и х_n-2 должны быть помещены симметрично внутри интервала L_n-2 на расстоянии L_n-2 от концов этого интервала. Следовательно, L_n-2 = L_n-1+L_n (pис.4, средняя часть).

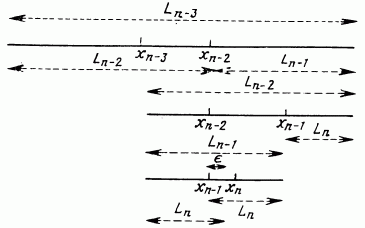
Рис. 4.

Замечание. Из рисунка ясно, что на предпоследнем этапе х_n-2 остается в качестве внутренней точки.

Аналогично L_n-3=L_n-2+L_n-1 (pис. 4, верхняя часть)

В общем случае L_j-1=L_j + L_j+1 при 1<j<n.

Таким образом,

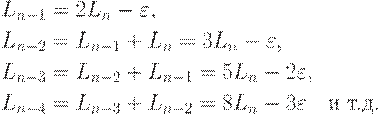
Если определить последовательность чисел Фибоначчи следующим образом: F₀=1, F₁=l, и F_k=F_k-1+F_k-2 для k = 2, 3,..., то

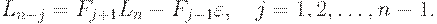(1)

Если начальный интервал (a;b) имеет длину L = (b-а), то

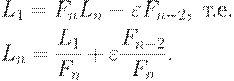( 2)

Следовательно, произведя n вычислений функции, мы уменьшим начальный интервал неопределенности в l/F_n раз по сравнению с его начальной длиной (пренебрегая е), и это - наилучший результат.

Если поиск начат, то его несложно продолжить, используя описанное выше правило симметрии. Следовательно, необходимо найти положение первой точки, которая помещается на расстоянии L₂ от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точкa помещается согласно правилу симметрии на расстоянии L₂ от второго конца интервала:

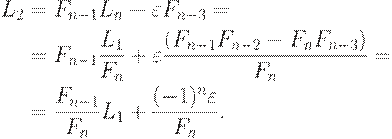( 3)

После того как найдено положение первой точки, числа Фибоначчи больше не нужны. Используемое значение е может определяться из практических соображений. Оно должно быть меньше L₁\F_n+x, в противном случае мы будем напрасно тратить время на вычисление функции.

Таким образом, поиск методом Фибоначчи, названный так ввиду появления при поиске чисел Фибоначчи, является итерационной процедурой. В процессе поиска интервала (x1; x2) с точкой х₂, уже лежащей в этом интервале, следующая точка х₂ всегда выбирается такой, что х₃–х₄ = х₂–х₁ или х₄-х₁ = х₃-x₂, т.е. x₄=х₁-х₂+х₃.

Если f(x₂) = f₂ и f(x₄) = f₄, то можно рассмотреть четыре случая (рис. 5).

Рис.5.

Следующий из методов одномерной оптимизаци называется методом "золотого сечения".

Не всегда можно заранее определить, сколько раз придется вычислять функцию. В методе Фибоначчи это нужно знать для определения L₂, т.е. положения начальной точки (см. уравнение 3).

Метод "золотого сечения" почти столь же эффективен, как и метод Фибоначчи, однако при этом не требуется знать n - количество вычислений функции, определяемое вначале. После того как выполнено j вычислений, исходя из тех же соображений, что и ранее (см. уравнение 1), записываем

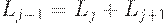( 4)

Однако если n не известно, то мы не можем использовать условие L_n-1 = L_n - е. Если отношение последующих интервалов будет постоянным, т.е.

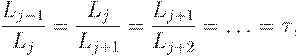( 5)

то

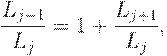
т.е.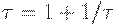

Таким образом, 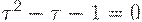, откуда 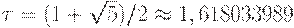. Тогда

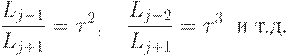
Следовательно, 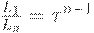, т.е.

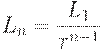( 6)

В результате анализа двух рассмотренных значений функции будет определен тот интервал, который должен исследоваться в дальнейшем. Этот интервал будет содержать одну из предыдущих точек и следующую точку, помещаемую симметрично ей. Первая точка находится на расстоянии L₁/t от одного конца интервала, вторая - на таком же расстоянии от другого. Поскольку

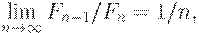
то из уравнения (3) видно, что поиск методом "золотого сечения" является предельной формой поиска методом Фибоначчи. Название "золотое сечение" произошло от названия отношения в уравнении (5). Видно, что L_j-1 делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому "золотому отношению".

Таким образом, если ищется интервал (х₀, х₃) и имеются два значения функции f₁ и f₂ в точках x₁ и x₂, то следует рассмотреть два случая (рис. 6).

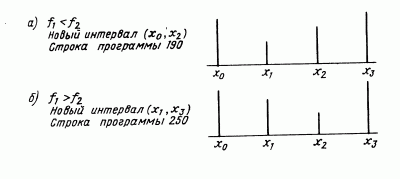
Рис. 6.

Метод гарантирует нахождение минимума в самых неблагоприятных условиях, однако он обладает медленной сходимостью.

Схема алгоритма метода "золотого сечения" представлена на рис.7

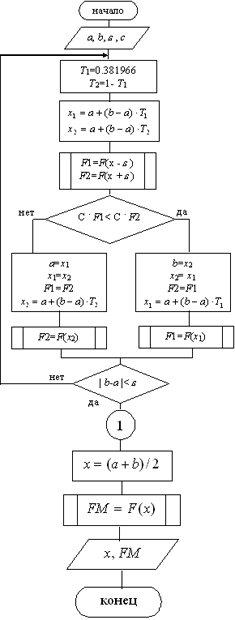
Рис. 7.Схема алгоритма метода "золотого сечения".

Здесь c - константа,

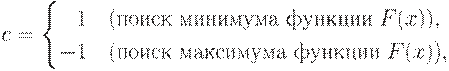
При выводе x - координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке.

Метод Ньютона

Следующий из рассматриваемых методов однопараметрической оптимизации является градиентным методом второго порядка. В нем при поиске экстремума целевой функции используется ее первые и вторые производные. Этот метод носит название метода Ньютона.

Метод применим для вогнутой (или выпуклой), функции F(x), что соответствует монотонности ее первой производной f(x).

Известно, что если функция F(x) имеет локальный минимум (или максимум) в точке 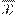, то в этой точке градиент функции F(x) (вектор ее производных) равен нулю, т.е.

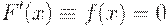
Следовательно, если функция F(x) дифференцируема, то для нахождения ее экстремума нужно решить уравнение

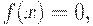( 7)

где 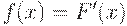. 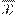- корень уравнения (3.1), точка, то есть, координата в которой F'(x)=0, а функция F(x) имеет минимум (или максимум) (рис.8).

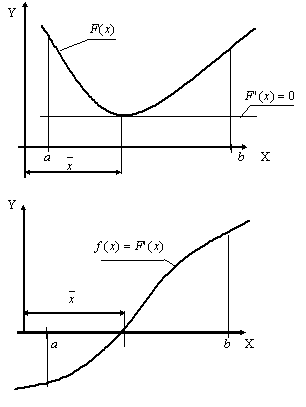
Рис. 8.Вогнутая функция F(x) и ее производная f(x).

Алгоритм метода Ньютона сводится к линейному представлению функции f(x) и решению уравнения (7).

Разложим функцию f(x) в ряд Тейлора:

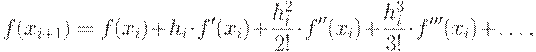
где h_i=x_i+1-x_i.

Отбросим члены ряда, содержащие .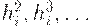

В результате имеем:

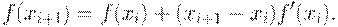
Если в точке (x_i+1) достигается экстремум функции F(x), то f(x_i+1)=0.

Тогда

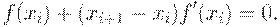
Отсюда точка экстремума равна:

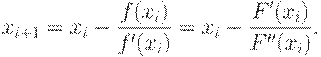( 8)

Для нахождения экстремума функции F(x) необходимо на каждом шаге итерационного процесса поиска определить первую F1 и вторую F2 производные целевой функции F(x), т.е.

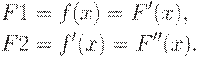
Начальные приближения х рекомендуется выбирать в той точке интервала [a,b], где знаки функции f(x) и ее кривизны f''(x) совпадают, т.е. выполняется условие

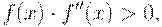( 9)

где

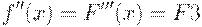
Словесный алгоритм метода Ньютона:

1. Выбираем начальную точку х. Если 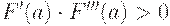,то x=a, иначе x=b.

2. Находим приближение корня (x_i+1) по выражению (8).

3. Итерационный процесс поиска продолжается до тех пор, пока

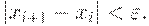( 10)

На основании (8) условие (10) можно записать как

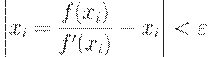
В результате условие (8) будет иметь вид

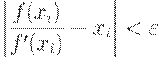
В точке экстремума 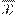производная 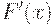меняет знак.

Если в точке 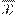функция F(x) имеет минимум, то производная 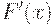в окрестности 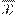меняет знак с отрицательного на положительный, т.е. 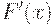является возрастающей функцией, значит, 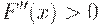(рис. 9 a).

Если в точке 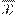функция F(x) имеет максимум, то производная 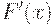в окрестности 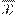меняет знак с положительного на отрицательный, т.е. 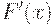является убывающей функцией, значит, 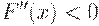(рис. 9 b).

Следовательно, по знаку 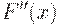можно судить: в точке 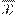максимум или минимум функции F(x).

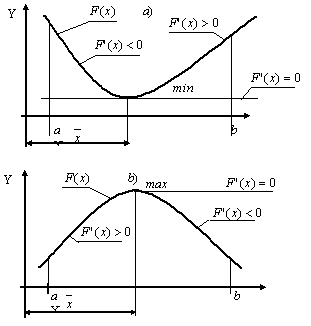
Рис. 9.

Если функция F(x) не дифференцируема или вычисление ее производных очень сложно, то для определения производных функции F(x) можно воспользоваться приблизительными оценками производных с помощью разностных схем: