Система дифференциальных уравнений

ТЕПЛОМАССООБМЕН

(часть 2)

Методические указания и контрольные задания

к самостоятельной работе студентов по

профилю подготовки «Теплогазоснабжение и вентиляция»

Составители А.Н. Козлобродов

Ю.Н. Кобякова

Т о м с к 2012

Тепломассообмен (часть 2): методические указания и контрольные задания / Сост. А.Н. Козлобродов, Ю.Н. Кобякова. – Томск: Изд-во Том. гос. архит.-строит. ун-та, 2012, − 44 с.

Рецензент к.т.н., доцент А.Н. Хуторной

Редактор Е.Ю. Глотова

Методические указания и контрольные задания по учебному курсу «Тепломассообмен», ч. 2, предназначены для организации самостоятельной работы студентов по направлению подготовки бакалавров 270800 « Строительство», профиль подготовки «Теплогазоснабжение и вентиляция» всех форм обучения.

Печатаются по решению методического семинара кафедры теплогазоснабжения. Протокол № 4 от 29 декабря 2011 г.

Утверждены и введены в действие проректором по учебной работе В. В. Дзюбо

с 12.01.2012

до 12.01.2017

Оригинал-макет подготовлен авторами.

Подписано в печать. Формат 60×84.

Бумага офсет. Гарнитура Таймс.

Уч.-изд. л 2,31. Тираж 60 экз. Заказ №

Изд-во ТГАСУ, 634003, г. Томск, пл. Соляная, 2.

Отпечатано с оригинал-макета в ООП ТГАСУ.

634003, г. Томск, ул. Партизанская, 15.

ОГЛАВЛЕНИЕ

Введение…………………………………………………….
1. Теоретическая часть……………………………………..
1.1. Конвективный теплообмен……………………………
1.1.1. Система дифференциальных уравнений конвективного теплообмена………………………
1.1.2. Критериальные уравнения конвективного теплообмена………………………………………...
1.1.3. Частные случаи конвективного теплообмена……
1.2. Теплообмен излучением………………………………
1.3. Теплообменные аппараты…………………………….
2. Примеры решения задач и задачи для самостоятельного решения……………………………
2.1. Примеры решения задач………………………………
2.2. Задачи для самостоятельного решения………………
Список рекомендуемой литературы………………………

ВВЕДЕНИЕ

Во второй части дисциплины «Тепломассообмен» рассматриваются два способа передачи тепла – конвективный и радиационный, или лучистый, теплообмены – и основы расчета теплообменных аппаратов.

Чтобы разобраться в этих способах передачи тепла, изучаются основные положения теорий: механизм переноса тепла в движущейся среде; свободное и вынужденное движение теплоносителя; ламинарный и турбулентный режимы течения; тепловой и гидродинамический пограничные слои; закон конвективной теплоотдачи (закон Ньютона–Рихмана); система уравнений конвективного теплообмена, состоящая из уравнения неразрывности, трех уравнений движения вязкого теплоноси-теля (уравнения Навье–Стокса), уравнения теплоотдачи в пог-раничном слое и уравнения переноса тепловой энергии; основы теории подобия; критериальные числа подобия Нуссельта (Nu), Пекле (Pe), Рейнольдса (Re), Грасгофа (Gr), Прандтля (Pr).

В предыдущем разделе курса при рассмотрении граничных условий третьего рода уже фигурировали закон Ньютона–Рихмана и коэффициент теплоотдачи, α численное значение которого считалось известным. Основной задачей раздела, посвященного конвективному механизму переноса теплоты движущейся средой (теплоносителем), является изучение методик определения коэффициента теплоотдачи и применения их для практических расчетов. Здесь можно выделить два пути решения проблемы.

Первый из них заключается в точном расчете α из уравнения теплоотдачи в пограничном слое с использованием уравнения переноса тепловой энергии и уравнения движения вязкого теплоносителя (уравнения Навье–Стокса). Такая про-цедура, связанная с решением нескольких дифференциальных уравнений, весьма трудоемка даже для современных компью-терных средств вычислений.

Второй путь определения коэффициента теплоотдачи базируется на физическом моделировании и обобщении экспериментальных данных с помощью теории подобия в виде критериальных уравнений теплоотдачи.

Решение задач, связанных с теплообменом излучением базируется на законах теплового излучения, основным из которых является закон Стефана–Больцмана.

Среди рассматриваемых типов теплообменных аппаратов наиболее распространенными являются рекуперативные теплообменники, поэтому при теоретическом анализе теплопередачи рассматриваются аппараты только этого типа.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Конвективный теплообмен

Конвективным теплообменом называется одновременный перенос теплоты конвекцией и теплопроводностью.

В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.

Самопроизвольное движение жидкости (газа) в поле тяжести, обусловленное разностью плотностей её горячих и холодных слоев, называют свободным движением (естественная конвекция).

Движение, создаваемое вследствие разности давлений, которые создаются насосом, вентилятором и другими устройствами, называется вынужденным (вынужденная конвекция).

Упорядоченное, слоистое, спокойное, без пульсаций движение называется ламинарным.

Беспорядочное, хаотическое, вихревое движение называется турбулентным.

Большое влияние на конвективный теплообмен оказывают следующие физические параметры: коэффициент теплопроводности (λ), удельная теплоемкость (с_р), плотность (ρ), коэффициент температуропроводности (а = λ/(ρ c_р), коэффициент динамической вязкости (μ) или кинематической вязкости (ν = μ/ρ), тεмпературный коэффициент объемного расширения (β = =1/(t+273)).

Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона–Рихмана, согласно которому количество теплоты, передаваемой конвективным теплообменом прямо пропорционально разности температур поверхности тела (t_'ст) и окружающей среды (t_'ж):

Q = α (t_'ст – t_'ж)·F , (1)

или

q = α (t_'ст – t_'ж) , (2)

где коэффициент теплоотдачи α [Вт/(м^{2 о}C)] характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Факторы, которые влияют на процесс конвективного теплообмена, включаются в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения:

α = f₁(Х; Ф; l_o; x_c; y_c; z_c; w_o; θ; λ; а; с_р; ρ; ν; β) , (3)

где Х – характер движения среды (свободная, вынужденная); Ф – форма поверхности; l_o – характерный размер поверхности (м) (длина, высота, диаметр и т. д.); x_c; y_c; z_c – координаты (м); w_o – характерная скорость течения (м/c); θ = (t_'ст – t_'ж) – температурный напор (^oС); λ – коэффициент теплопроводности Вт/(м²·^oС); а – коэффициент температуропроводности (м²/с); с_р – изобарная удельная теплоемкость (Дж/(кг·^oС); ρ – плотность (кг/м³); ν – коэффициент кинематической вязкости (м²/с); β – температурный коэффициент объемного расширения (1/ ^oС).

Уравнение (3) показывает, что коэффициент теплоотдачи величина сложная, и для её определения невозможно получить общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования.

Достоинством экспериментального метода является достоверность получаемых результатов.

Основной недостаток этого метода в том, что результаты конкретного эксперимента не могут быть использованы для другого явления, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.

Система дифференциальных уравнений

Конвективного теплообмена

Для исследования конвективного теплообмена при условии, что жидкость является несжимаемой и плотность среды ρ=const, нужно решить систему дифференциальных уравнений, состоящую из:

1) уравнения неразрывности, выражающего закон сохранения массы:

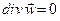; (4)

2) уравнений движения, выражающих закон сохранения импульса:

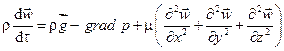; (5)

3) уравнения энергии, выражающего закон сохранения энергии:

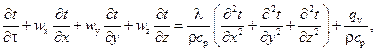(6)

где q_v – мощность тепловыделения внутренних источников тепла.

4) уравнение теплообмена (условие теплообмена на границе твердого тела и среды):

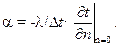(7)

Для получения единственного решения системы дифференциальных уравнений (4) –(7) необходимо задать условия однозначности, которые включают: геометрию расчетной области, ее размеры и время процесса; физические свойства текучей среды; закон изменения внутренних источников теплоты (в частном случае, 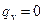); начальные и граничные условия.

Начальные условия определяют распределение температуры, скорости, и давления в начальный момент времени процесса конвективного теплообмена во всей расчетной области:

;

;

.

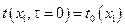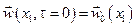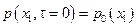Граничные условия для уравнения энергии могут иметь вид граничных условий I, II, III и IV родов на твердых ограничивающих течение жидкости поверхностях. Например, граничные условия IV рода в этом случае имеют вид

,

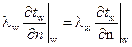где 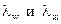– коэффициенты теплопроводности ограждений и текучей среды; n – нормаль к поверхности теплообмена.

Скорость на твердых, ограничивающих текучую среду поверхностях равна нулю в силу условия прилипания. На свободных поверхностях расчетной области скорость должна быть либо задана, либо рассчитана в ходе итерационного процесса.

Для расчета поля давления на твердых ограничивающих поверхностях, как правило, задают граничное условие

.

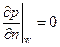Критериальные уравнения

Конвективного теплообмена

Используя теорию подобия из системы дифференциальных уравнений (4) – (7), можно получить уравнение теплоотдачи (7) для конвективного теплообмена в случае отсутствия внутренних источников тепла в следующей критериальной форме:

Nu = f (Х; Ф; X₀; Y₀; Z₀; Re; Gr; Pr) , (8)

где X₀; Y₀; Z₀ – безразмерные координаты; Nu= α ·l₀/λ – критерий Нуссельта (безразмерный коэффициент теплоотдачи), характеризует теплообмен между поверхностью стенки и жидкостью (газом); Re = w₀·l₀/ν – критерий Рейнольдса, характеризует соотношение сил инерции и вязкости и определяет характер течения жидкости (газа); Gr = (β·g·l₀³·Δt)/ν² – критерий Грасгофа, характеризует подъемную силу, возникающую в жидкости (газе) вследствие разности плотностей; 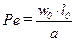– критерий Пекле, является мерой соотношения конвективного и молекулярного переносов теплоты в потоке; Pr = ν/а = (μ·c_p)/λ – критерий Прандтля, характеризует физические свойства жидкости (газа); l₀ – характерный линейный размер (длина, высота, диаметр); w_0. – характерная скорость течения.

Частные случаи конвективного теплообмена

1. Теплообмен при движении жидкости в трубах

Гидродинамические исследования показывают, что в гладких цилиндрических трубах при значениях числа Рейнольдса менее 2300 поток движется ламинарно, а при 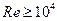наблюдается развитый турбулентный режим течения. Промежуточный между ламинарным и турбулентным, так называемый переходный режим течения, является неустойчивым и зависит от внешних воздействий (чистоты жидкости и шероховатости поверхности). Следует отметить, что границы перехода от одного режима к другому не зависят от того, какая жидкость или газ протекают в трубах – это может быть вода, воздух, бензин и пр. Поэтому в дальнейшем словом «жидкость» будет определяться любая текучая среда.

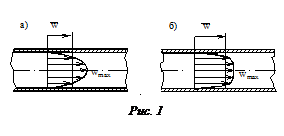На рис. 1 показаны профили скорости по поперечному сечению трубы при ламинарном (а) и турбулентном (б) режимах движения потока. Для ламинарного движения отношение средней скорости 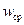к максимальной 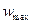составляет примерно 0,5, а для турбулентного режима, где изменение скорости потока происходит в основном в пределах гидродинамического пограничного слоя, это отношение 0,8. Различие в гидродинамике потока, естественно, отражается и на процессе конвективного теплообмена.

Для ламинарного режима

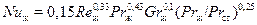; (9)

для развитого турбулентного режима

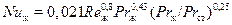; (10)

для переходного режима

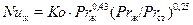, (11)

где численное значение комплекса Kо определяется из табл. 1 в зависимости от числа Рейнольдса.

Таблица 1

Re 103	2,1	2,2	2,3	2,4	2,5	3,0	4,0	5,0	7,5
Ko	1,9	2,2	3,3	3,8	4,4	6,0	10,3	15,5	24,4	33,3

В вышеприведенных формулах индекс «ж» показывает, что физические характеристики жидкости (кинематическую вязкость, плотность, теплоемкость и др.), входящие в числа подобия, следует определять при температуре жидкости, а индекс «ст» говорит об определяющей температуре стенки. Определяющей скоростью в этих формулах принята средняя по сечению скорость потока, а определяющим линейным размером является внутренний диаметр трубы d.

Для некруглых труб за определяющий линейный размер принимается эквивалентный диаметр

,

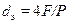где F – площадь поперечного сечения канала, Р – смоченный периметр сечения.

При теплообмене между потоком и стенкой в коротких трубах, когда длина трубы L меньше 50 диаметров, полученное значение числа Нуссельта следует умножить на поправочный коэффициент, значение которого приведены в табл. 2.

Таблица 2

L/d
Re = 2×103	1,90	1,70	1,44	1,28	1,18	1,13	1,05	1,02	1,00
Re = 2×104	1,51	1,40	1,27	1,18	1,13	1,10	1,05	1,02	1,00
Re = 1×105	1,28	1,22	1,15	1,10	1,08	1,06	1,03	1,02	1,00

При движении жидкости в винтовых змеевиках (рис. 2, а) возникает дополнительная циркуляция потока, что приводит к увеличению коэффициента теплоотдачи. В области развитой турбулентности при значениях ,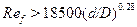

где D – диаметр спирали, коэффициент теплоотдачи, определяемый для прямой трубы, умножается на поправочный коэффициент e_D, который подсчитывается по формуле

e_D = 1 + 3,6 d/D. (12)

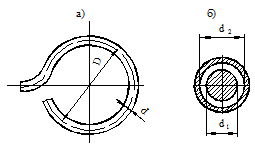
При движении потока в кольцевых каналах (рис. 2, б) теплоотдача определяется выражением

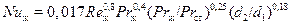, (13)

где d₁ – внутренний диаметр канала, d₂ – наружный диаметр канала, а определяющим размером является разность диаметров

d = d₂ – d₁.

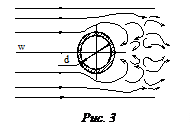
2. Теплоотдача при поперечном обтекании одиночной трубы

Картина обтекания потоком цилиндрической трубы показана на рис. 3. Так как скорость обтекания в различных точках цилиндра неодинакова, коэффициент теплоотдачи по периметру будет так же различен.

В практических расчетах локальные значения коэффициента теплоотдачи требуются редко, поэтому ниже приведены формулы, справедливые для осредненных значений чисел Нуссельта и, соответственно, коэффициентов теплоотдачи для всей поверхности трубы при:

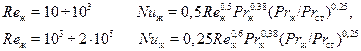(14)

В этих формулах определяющими приняты: скорость набегающего потока, температура набегающего потока, наружный диаметр трубы.

В том случае, когда угол атаки набегающего потока по отношению к оси трубы отличен от 90°, значение числа Нуссельта следует умножить на поправочный коэффициент, указанный в табл. 3.

Таблица 3

Угол атаки, град.
Коэффициент	1,00	0,98	0,83	0,64	0,60

3. Теплоотдача в пучках труб

Многие теплообменные аппараты состоят не из одиночных поверхностей или труб, а составлены из трубных пучков.

Расположение труб в пучке относительно друг к другу может быть различным, и от этого зависят условия обтекания труб, что влияет на коэффициент теплоотдачи. Чаще всего рассматривают шахматное (а) и коридорное (б) расположение труб в пучке (рис. 4). Поперечный S₁ и продольный S₂ шаги между трубами зависят от конструктивных особенностей теплообменника и выбираются в каждом конкретном случае по различным

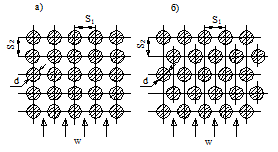опытным данным.

Для шахматного пучка рекомендуются следующие расчетные выражения:

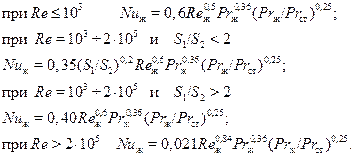(15)

В случае коридорного расположения труб в пучке используются следующие формулы:

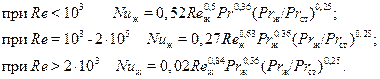(16)

В этих формулах определяющим размером является наружный диаметр трубы, а определяющей скоростью – скорость потока в самом узком сечении пучка. Симплекс 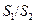характеризует особенности геометрии пучка.

Все вышеприведенные формулы справедливы для третьего и последующих рядов труб, где поток считается установившимся и коэффициент теплоотдачи постоянным. Коэффициент теплоотдачи для труб первого ряда составляет 0,6 от найденного по формулам (15)–(16). Для труб второго ряда этот поправочный коэффициент равен0,7для шахматного расположения труб и 0,9 – для коридорного. Средний коэффициент теплоотдачи для всего пучка, состоящего из z рядов, определяется по формулам: для шахматного пучка – 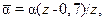для коридорного пучка – .

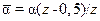4. Теплоотдача при вынужденном движении потока вдоль горизонтальной пластины

При ламинарном режиме течения потока (при 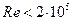) рекомендуется следующая формула:

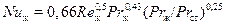. (17)

В случае турбулентного движения жидкости (при )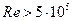

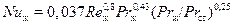. (18)

Определяющим линейным размером в этих формулах является длина пластины в направлении потока, а определяющей скоростью – средняя скорость потока.

5. Теплоотдача при естественной конвекции

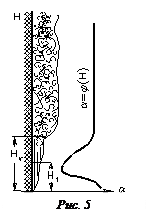Если температура стенки превышает температуру жидкости или газа, находящихся около стенки, то в самой среде возникает естественная конвекция из-за различия в плотности неодинаково нагретой среды.

На рис. 5 показано, изменение коэффициента теплоотдачи при свободной конвекции около вертикальной пластины или трубы.

При числе Рэлея менее 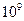процесс протекает в области, соответствующей высоте 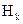и для этого режима теплоотдача определяется по формуле

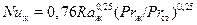. (18)

При значениях 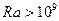наблюдается и ламинарное, и турбулентное течение.

В этом случае вначале определяется критическая высота

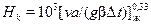. (19)

На оставшемся участке с турбулентным режимом движения потока коэффициент теплоотдачи a_т определяется по формуле

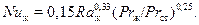(20)

Средний по высоте коэффициент теплоотдачи при наличии ламинарного и турбулентного участков пограничного слоя на вертикальной поверхности определяется по выражению

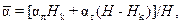(21)

где 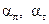– коэффициенты теплоотдачи ламинарного и турбулентного участков.

6. Теплоотдача при кипении и конденсации

В термодинамике процессы парообразования и конденсации рассматривались как равновесные. Условно принималось, что жидкая и парообразная фазы в процессе изменения агрегатного состояния находятся при одинаковой температуре насыщения 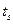, однозначно определяемой давлением. Но эти процессы сопровождаются интенсивным теплообменом, который возможен только при наличии температурного градиента. Установлено, что первоначально пузырьки пара при кипении образуются не в толще жидкости, а на поверхностях нагрева в отдельных точках, называемых центрами парообразования. Размер образовавшихся паровых пузырьков постепенно увеличивается. Из-за меньшей плотности пара действующая вверх сила в какой-то момент становится больше сил сцепления пузырька с поверхностью, и он всплывает. Частота появления пузырьков в центрах парообразования и число действующих центров увеличивается с ростом температурного напора

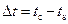, (22)

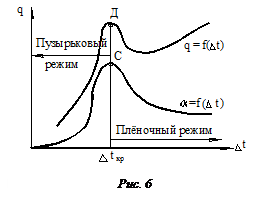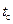где – температура стенки.

Это ведёт к увеличению коэффициента теплоотдачи и плотности теплового потока, как показано на рис. 6. Интенсивность пузырькового кипения возрастает до определенного предела, когда количество центров парообразования становится так много, что паровые пузырьки сливаются и образуют сплошную паровую пленку с большим термическим сопротивлением. В отличие от пузырькового такой режим кипения называется пленочным. При проектировании парогенераторов следует создавать такие условия, в которых бы не допускался пленочный режим кипения. При р = 0,1 МПа критический тепловой поток для воды равен q_кр =(1,1–1,6) 10⁶ Вт/м². С увеличением давления до 6–7 МПа критический тепловой поток возрастает до 4 10⁶ Вт/м², а затем уменьшается.

При пузырьковом кипении жидкости в условиях естественной конвекции коэффициент теплоотдачи определяется как

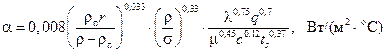, (23)

где l – коэффициент теплопроводности жидкости, m – коэффициент динамической вязкости жидкости, с – теплоёмкость жидкости, t_s – термодинамическая температура насыщения, r – удельная теплота парообразования, r_п – плотность пара, r – плотность жидкости, s – коэффициент поверхностного натяжения.

Для определения коэффициента теплоотдачи в условиях пузырькового кипения воды при давлении от0,1до 4,0МПа рекомендуется такая упрощенная расчетная формула:

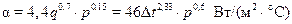. (24)

При определении коэффициентов теплоотдачи при кипении некоторых хладонов в трубах испарителей используется следующая эмпирическая формула

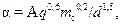Вт/(м²· ^oC), (25)

где m_c – массовый секундный расход хладона, кг/ч; d – внутренний диаметр трубы, м; А – коэффициент, значения которого даны в табл. 4.

Таблица 4

Холодильный агент	А 103 при ts
10 °C	–10 °C
Хладон-22 Хладон-12 Хладон-142	5,84 4,46 3,67	5,00 3,83 3,30

При соприкосновении насыщенного пара с более холодной стенкой происходит конденсация – фазовый переход, сопровождающийся выделением теплоты.

Различают капельную и пленочную конденсацию. В первом случае конденсат осаждается на стенку в виде капель, а во втором – в виде сплошной пленки.

Движение пленки под действием гравитационных сил может быть ламинарным и турбулентным. Характер движения на вертикальной пластине или трубе характеризуется безразмерным числом

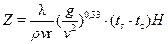, (26)

где Н – высота стенки, м.

При Z<2300 движение пленки ламинарное и для этого случая

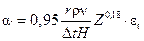. (27)

При Z>2300течение пленки ламинарное вверху и турбулентное внизу:

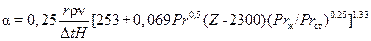. (28)

Если конденсация пара происходит на горизонтальных трубах, то для ламинарного режима, преимущественного в этом случае,

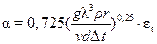, (29)

где d – наружный диаметр трубы, м.

Поправка, учитывающая зависимость физических свойств конденсата от температуры в формулах (27) и (29), определяется

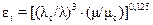. (30)

Теплообмен излучением

Тепловое излучение (радиационный или лучистый теплообмен) – это распространение через газовый слой внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются электрически заряженные частицы, входящие в состав тела. Всякое тело, имеющее температуру 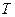, отличную от абсолютного нуля, способно излучать лучистую энергию, т. е. наряду с потоком энергии от более нагретых тел к менее нагретым всегда имеется и обратный поток энергии от менее нагретых тел к более нагретым. Конечный результат этого обмена и представляет количество теплоты, передаваемой излучением. Наиболее наглядным примером лучистого теплообмена является излучение Землей теплоты от Солнца (солнечная радиация). Существуют различные виды электромагнитного излучения: 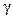-излучение, рентгеновское излучение, радиоволны и др. Однако способностью трансформироваться в теплоту (повышать внутреннюю энергию облучаемого тела) обладает излучение светового диапазона (длина волн 0,4–0,8 мкм) и в наибольшей мере инфракрасного диапазона. С увеличением температуры тела тепловое излучение увеличивается, т. к. увеличивается внутренняя энергия тела.

Большинство твердых и жидких тел излучают энергию всех длин волн в интервале от 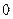до 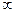, т. е. имеют непрерывный спектр излучения. Газы, испускают энергию только в определенном интервале длин волн (селективный спектр излучения). Лучистый поток, излучаемый с единицы поверхности тела по всем направлениям полусферического пространства, называется плотностью излучения 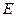, Вт/м 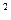. Если величина 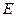одинакова для всех элементов поверхности 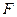, то полный тепловой поток 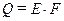, Вт.

Если на тело падает лучистый поток 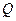, то часть этого потока 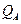будет поглощаться телом, часть 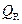– отражаться, а часть 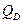– проходить сквозь него: 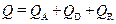. Поделив это равенство на величину 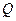, получим соотношение коэффициентов поглощения 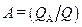, отражения 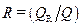и прозрачности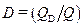

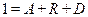. (31)

Для абсолютно черного тела 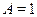и 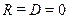; для абсолютно белого тела 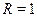и 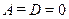; для абсолютно прозрачных тел 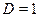и .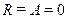

Большинство твердых и жидких тел для тепловых лучей практически непрозрачны, т. е. для них 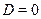и .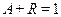

Одно- и двухатомные газы практически прозрачны для теплового излечения. Трех- и многоатомные газы обладают селективной способностью излучать и поглощать энергию.

Участвующее в лучистом теплообмене тело (например, твердое), помимо собственного излучения 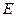отражает падающую на него энергию в количестве 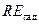. Сумма энергии собственного отраженного излучения составляет эффективное излучение тела:

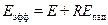. (32)

Для расчета лучистого теплообмена между телами важное значение имеет результирующее излучение, представляющее разность между потоком, получаемым телом, и потоком, которое оно испускает. Плотность результирующего излучения

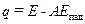. (33)

Закон Планка устанавливает зависимость интенсивности излучения от температуры Т и длины волны λ: при всех температурах интенсивность излучения равна нулю пр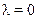и и 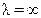, а при некотором промежуточном значении 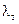имеет максимум; для всех длин волн интенсивность излучения тем выше, чем выше температура.

Длину волны, которой соответствует максимум теплового излучения, согласно закону Вина, можно найти из условия, (мкм) 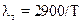. Следовательно, с повышением температуры максимум излучения смешивается в сторону более коротких волн.

Согласно закону Стефана–Больцмана, плотность потока собственного излучения абсолютно черного тела (как результат суммирования интенсивности излучения по всем длинам волн)

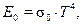(34)

где 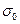− постоянная излучения абсолютно черного тела ( 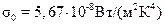). Для практических расчетов (34) приводят к виду 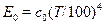, где .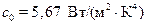

Спектры излучения реальных тел отличны от спектра излучения абсолютно черного тела. При этом интенсивность излучения тела на любой длине волны никогда не превышает соответствующую интенсивность излучения абсолютно черного тела. Частным случаем реальных тел являются серые тела, спектр излучения которых подобен спектру излучения черного тела. В практике расчетов с определенной степенью точности реальные тела считают серыми, для которых закон Стефана–Больцмана имеет вид

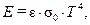(35)

где 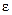− коэффициент излучения (степень черноты) серого тела; всегда .

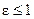Согласно закону Кирхгофа, отношение излучательной способности к поглощательной при температурном равновесии не зависит от природы тела, т. е. поглощательная способность численно равна степени черноты тела: .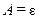

C помощью закона Стефана–Больцмана можно определить общее количество энергии, излучаемое телом по всем возможным направлениям. Однако распределение этой энергии по разным направлениям оказывается неодинаковым. Согласно закону Ламберта, количество энергии 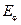, излучаемой теплом в направлении, составляющем с нормалью к поверхности угол 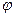, определяется по уравнению

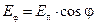. (36)

Опыт показывает, что закон Ламберта строго справедлив только для абсолютно черного тела. У серых тел этот закон подтверждается лишь в пределах .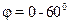

Применение законов лучистого теплообмена и представление об эффективной плотности теплового потока позволяют найти расчетные зависимости для результирующего теплового потока между твердыми телами, разделенными прозрачной средой (D = 1).

Тепловой поток между двумя параллельными пластинами 1 и 2 неограниченных размеров ( 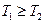), Вт:

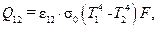(37)

где 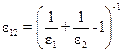− приведенная степень черноты системы; площадь пластины .

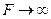Тепловой поток между двумя телами, одно из которых находится в полости (оболочке) другого тела; поверхность внутреннего тела F₁ – выпуклая, внешнего F₂ – вогнутая; температура внутреннего тела Т₁, а внешнего Т₂, причем Т₁>Т₂:

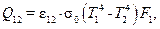(38)

где 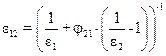; 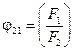− угловой коэффициент излучения, характеризующий часть излучения внешней поверхности, попадающей на внутреннюю. Если 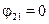то

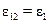. (39)

В реальных условиях эксплуатации различных технических систем теплота может одновременно передаваться теплопроводностью, конвекцией и излучением. Такой теплообмен называют сложным.

Если газообразная среда прозрачна для тепловых лучей (D=1), то расчет теплообмена осуществляют, используя принцип аддитивности (суммирования) тепловых потоков за счет отдельных способов (механизмов) теплообмена. В наиболее общем случае радиационно-конвективной теплоотдачи величина теплового потока Q от стенки к омывающему ее газу и к окружающим телам путем соответственно конвективной теплоотдачи Q_к и теплового излучения Q_р через прозрачный газ, Вт,

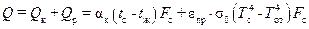, (40)

где 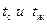− температура соответственно стенки и газа за пределами пограничного слоя; 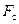− площадь поверхности теплообмена стенки; 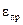− приведенная степень черноты системы; 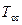− температура окружающих тел (оболочки).

Если газовый объем ограничен стенками и его толщина соизмерима с толщиной пограничных слоев, то теплообмен рассматривают как радиационно-кондуктивный и в расчете учитывают метод эквивалентной теплопроводности, рассмотренный выше.

Теплообменные аппараты

Теплообменными аппаратами называют технические устройства, предназначенные для передачи теплоты от одного теплоносителя к другому. Теплообменными аппаратами являются: парогенераторы и конденсаторы паротурбинных установок, испарители и конденсаторы холодильных машин, промежуточные охладители компрессорных установок и многие другие устройства. Участвующие в теплообмене вещества (теплоносители) могут находиться в жидком или газообразном состоянии либо в виде двухфазного потока.

По принципу действия теплообменные аппараты делятся на рекуперативные, регенеративные и смесительные (или контактные). В рекуператорах обеспечивается передача тепла от горячего теплоносителя к холодному через разделяющую их стенку (по конструктивному исполнению рекуператоры бывают самыми разнообразными: кожухотрубными, радиаторными, пластинчыми, спиральными, сотовыми, витыми и многими другими). В регенераторахгорячий и холодный теплоносители омывают одну и ту же поверхность теплообмена (теплоемкую аккумулирующую насадку), например, воздухоподогреватели доменных печей, регенераторы разделения воздуха и др. Режим работы регенераторов обычно нестационарный. В смесительных аппаратах передача тепла между теплоносителями осуществляется путем непосредственного их смешивания (контакта). Часто контактный теплообмен сопровождается массообменом, например, в градирнях, скрубберах, эжекторах и др.

Кроме перечисленных, существует множество их разновидностей, применяемых в технике.

Наиболее широкое применение находят рекуперативные теплообменные аппараты различного назначения.

Тепловой расчет рекуператоров может быть проектным, целью которого является определение поверхности теплообмена, и поверочным, в результате которого при известной поверхности нагрева Fо пределяются количество передаваемой теплоты (тепловая мощность Q) и конечные температуры теплоносителе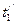й и 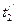. Основными расчетными уравнениями являются:

– уравнения теплового баланса (уравнения I закона термодинамики), которые при отсутствии тепловых потерь от корпуса аппарата имеют вид

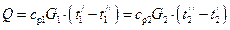, (41)

где нижний индекс «1» и «2» относятся соответственно к горячему и холодному теплоносителю; верхние индексы « ^/ » и «^// » – к параметрам теплоносителей на входе и выходе. Очевидно, что при работе в стационарном режиме массовые расходы 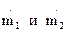теплоносителей постоянны по длине теплообмена.

Третьим расчетным уравнением является основное соотношение теплопередачи, которое при условии 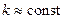, представляется как

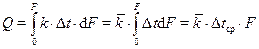, (42)

где 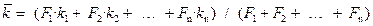– средний коэффициент теплопередачи; 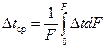– средний температурный напор между теплоносителями.

Величина 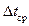зависит от схемы движения теплоносителей. Наиболее простыми схемами являются: прямоток, противоток и перекрестный ток. При прямотоке теплоносители движутся вдоль поверхности теплообмена в одном направлении, при противотоке – в противоположных направлениях, при перекрестном токе – в перекрещивающихся направлениях. Во многих аппаратах схемы намного более сложные. При противотоке можно обеспечить более высокое значение среднего температурного напора 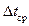, что является достоинством этой схемы в ряде случаев. Если необходимо поддерживать постоянную температуру на поверхности нагрева ( 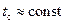), то предпочтение отдают прямоточным схемам (рис. 7). Средний температурный напор для прямотока и противотока определяют как

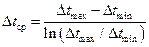, (43)

где 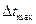– максимальный, а 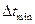– минимальный температурный напор (например, для прямотока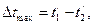 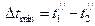, а для противотока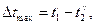

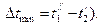
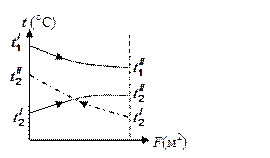
Около 80 % энергии в промышленности передается в различных теплообменных аппаратах и поэтому центральной задачей при их проектировании является экономия материальных и экономических ресурсов. При этом необходимо учитывать, что с уменьшением металлоемкости аппарата снижаются капитальные затраты, но одновременно с этим растут энергетические затраты при эксплуатации, связанные с ростом скоростей или температурных напоров. Так, например, повышение скорости теплоносителя позволяет повысить коэффициент теплоотдачи и, соответственно, коэффициент теплопередачи аппарата, а следовательно, уменьшить габариты и металлоемкость. Однако при этом возрастают потери напора и расход мощности на привод насоса или компрессора.

Повышение эффективности теплообменных систем предполагает: 1) уменьшение поверхности или увеличение производительности при заданных условиях работы; 2) уменьшение температурного напора 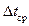при заданных площади поверхности теплообмена F и производительности (тепловой мощности 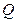). Эти задачи могут быть решены путем повышения коэффициента теплопередачи .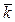