Центра скоростей плоской фигуры
Мгновенный центр скоростей плоской фигуры
Определение: Точка, неизменно связанная с плоскостью фигуры, скорость которой в данный момент равна нулю, называется мгновенным центром скоростей.
Теорема существования мгновенного центра скоростей: Мгновенный центр скоростей существует, если в рассматриваемый момент времени плоская фигура не совершает поступательного движения.
Доказательство: см. ИОС
Теорема о проекциях скоростей точек
Плоской фигуры
Теорема: Проекции скоростей двух точек плоской фигуры на прямую, проходящую через эти две точки, равны.
Доказательство: см. ИОС
Определение скоростей точек плоской фигуры
С помощью мгновенного центра скоростей
Определим скорости точек плоской фигуры В и D на основании формулы (4.2), выбрав в качестве полюса мгновенный центр скоростей Рv:
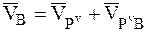 ,
, 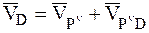 .
.
Так как 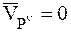 , то
, то 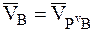 ,
, 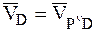 , поэтому для скоростей точек плоской фигуры В и D получим:
, поэтому для скоростей точек плоской фигуры В и D получим:
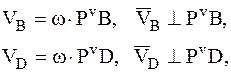
т.е. скорость любой точки плоской фигуры в данный момент времени представляет собой скорость вследствие вращательного движения плоской фигуры вокруг мгновенного центра скоростей, который является и мгновенным центром вращения (рис. 20).
Найдем зависимость между скоростями точек плоской фигуры в рассматриваемый момент времени, используя тот факт, что угловая скорость плоской фигуры одинакова для всех точек плоской фигуры в каждый момент времени:
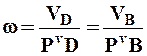 , (7.3) или
, (7.3) или 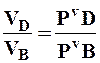 . (7.4)
. (7.4)
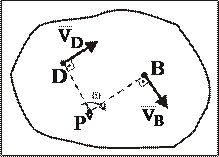
Рис. 20
Модули скоростей точек плоской фигуры в каждый момент времени пропорциональны расстояниям от этих точек до мгновенного центра скоростей.
Для того чтобы определить скорости точек плоской фигуры с помощью мгновенного центра скоростей, необходимо сначала найти положение мгновенного центра скоростей.
Способы определения положения мгновенного
центра скоростей плоской фигуры
Существует несколько способов определения положения мгновенного центра скоростей:
7.9.1. Если плоская фигура катится без скольжения и проскальзывания по неподвижной поверхности, тогда мгновенный центр лежит в точке соприкосновения фигуры и неподвижной поверхности (рис. 21).

Рис.21
7.9.2. Если известны в данный момент времени непараллельные прямые, по которым направлены скорости двух точек плоской фигуры В и D, то мгновенный центр скоростей плоской фигуры определяется как точка пересечения перпендикуляров, восстановленных в точках плоской фигуры D и В к этим прямым (рис. 22).
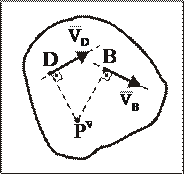
Рис. 22
7.9.3. Если известны в данный момент времени скорости точек плоской фигуры В и D, которые параллельны между собой и при этом лежат на общем перпендикуляре к скоростям этих точек, то мгновенный центр скоростей плоской фигуры определяется как точка пересечения прямых, проведенных через начала и концы векторов скоростей 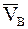 и
и 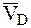 независимо от того направлены они в одну или разные стороны (рис. 23).
независимо от того направлены они в одну или разные стороны (рис. 23).
Если 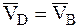 (равны по величине и совпадают по направлению), то мгновенный центр скоростей будет находиться в бесконечности и
(равны по величине и совпадают по направлению), то мгновенный центр скоростей будет находиться в бесконечности и 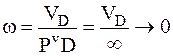 , т.е. плоская фигура совершает мгновенное поступательное движение.
, т.е. плоская фигура совершает мгновенное поступательное движение.
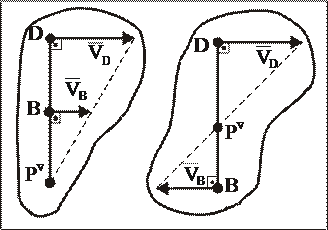
Рис. 23
7.9.4. Если скорости точек плоской фигуры В и D параллельны и не перпендикулярны к ВD в данный момент времени, то мгновенный центр скоростей плоской фигуры находится в бесконечности, т.е. плоская фигура совершает мгновенное поступательное движение и скорости всех ее точек равны (рис. 24).
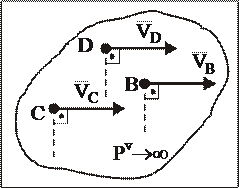
Рис. 24
