Рішення задачі безумовної оптимізації методом Ейлера
Всі методи рішення задачі безумовної оптимізації можна розділити на два класи: класичні і прямого пошуку.
Класичні методи, які в літературі ще називають непрямими, точними або непрямими, дозволяють знайти оптимальну крапку непрямим шляхом – через вирішення системи рівнянь, в загальному випадку нелінійної. При цьому, якщо вирішення системи проводиться не наближеними методами, то набувають точних значень координат екстремальних точок функції, що оптимізується.
Методи прямого пошуку, які також називають просто прямими, пошуковими, покроковими, ітераційними, обчислювальними, наближеними або некласичними, вирішують задачу безумовної оптимізації шляхом поступового поетапного наближення до точки екстремуму. Рішення отримують наближеним, але з наперед заданою точністю.
Розглянемо класичний метод рішення задачі безумовної оптимізації, який носить назву метод Ейлера. Метод дозволяє виявити всі екстремальні точки функції (як локальні мінімуми, так і локальні максимуми), що оптимізується, і таким чином дати загальне уявленні про поведінку гіперповерхні функції 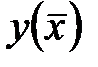 у гіперпросторі
у гіперпросторі 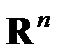 .
.
Метод Ейлера заснований на використанні необхідних і достатніх умовах існування екстремуму.
Алгоритм методу полягає в наступному.
1. Беруть часткові похідні функції, що оптимізується 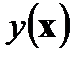 по кожній змінній хi і, відповідно до необхідної умови для точки локального екстремуму, прирівнюють нулю:
по кожній змінній хi і, відповідно до необхідної умови для точки локального екстремуму, прирівнюють нулю: 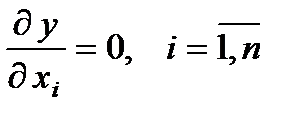 ;
;
2. Вирішують будь-яким відомим методом отриману систему, що складається з n в загальному випадку нелінійних рівнянь. Корені системи, якщо вони існують, є стаціонарними точками функції 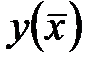 оскільки в них всі приватні похідні дорівнюють нулю.
оскільки в них всі приватні похідні дорівнюють нулю.
3. Беруть всі другі приватні і змішані похідні від функції 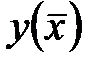 і обчислюють їх в кожній стаціонарній крапці. По обчислених похідних формують матрицю Гесса для кожної стаціонарної крапки.
і обчислюють їх в кожній стаціонарній крапці. По обчислених похідних формують матрицю Гесса для кожної стаціонарної крапки.
4. Досліджують характер матриць Гесса і встановлюють вид відповідних стаціонарних точок:
¨ при позитивній визначеності матриці визначена точка мінімуму;
¨ при негативній – локальний максимум;
¨ при напіввизначеності – залишають стаціонарну точку для додаткових досліджень;
¨ при невизначеності – сідловою точкою.
5. Обчислюють значення функції 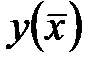 у кожному локальному мінімумі. Потім шляхом порівняння обчислених значень знаходять абсолютний мінімум функцій.
у кожному локальному мінімумі. Потім шляхом порівняння обчислених значень знаходять абсолютний мінімум функцій.
Хід роботи
Побудуйте блок-схему знаходження локального мінімуму методом Ейлера для функції двох змінних 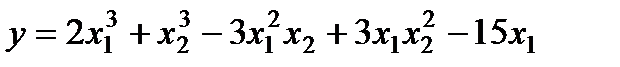
Контрольні запитання.
1. Назвіть необхідні умови існування екстремуму функції.
2. В якому випадку стаціонарна точка являється локальним мінімумом, максимумом?
