Результаты численного исследования динамики системы Лоренца

При σ = 10, β = 8/3. (ρ* ≈ 24.74) ДС Лоренца имеет следующую зависимость координат от времени (рис. 1) и следующий фазовый портрет (рис. 2)

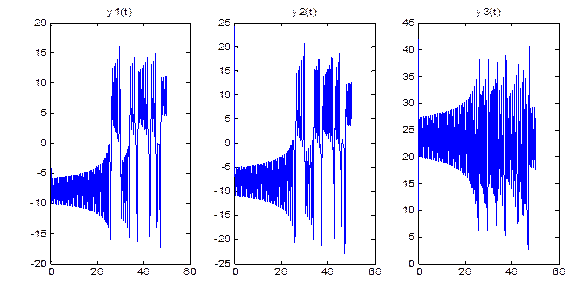
Рис. 1.

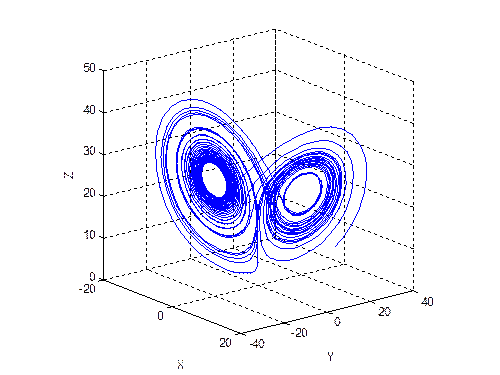
Рис. 2.

1) 1 ≤ ρ < ρ1 ≈ 13.926..

• т. О – неустойчивая,

• точки О_1,2 – устойчивые (бистабильность). Зависимость от начальных условий. Две ветви сепаратрисы - Г₁ и Г₂

При ρ = 13.926..ДС Лоренца имеет следующую зависимость координат от времени (рис. 3) и следующий фазовый портрет (рис. 4)

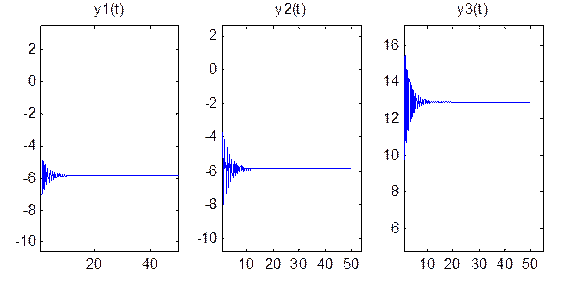
Рис. 3.

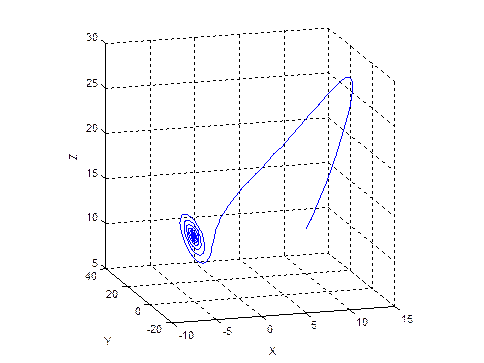
Рис. 4.

При ρ > ρ₃ ≈ 148.4

Одно притягивающее множество - предельный цикл (автоколебания).

При уменьшении параметра ρ от ρ₃ к ρ* переход к хаосу:

- через каскад бифуркаций удвоения периода.

- через перемежаемость

ДС Лоренца имеет следующую зависимость координат от времени (рис. 5) и следующий фазовый портрет (рис. 6)

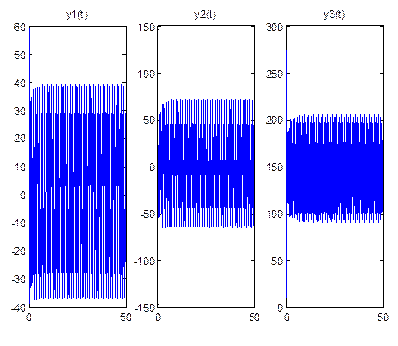
Рис. 5.

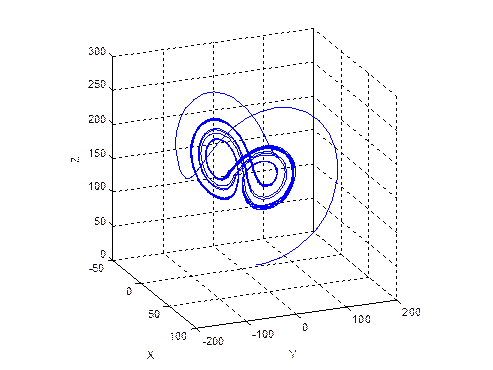
Рис. 6.

Дополнительная литература

• Анищенко В.С. Детерминированный хаос // Соросовский образовательный журнал, 1997, №6, с.70-76.

• Анищенко В.С. Динамические системы // Соросовский образовательный журнал. 1997,№11, с.77-84.

• Анищенко В.С. Устойчивость, бифуркации, катастрофы // Соросовский образовательный журнал, 2000, №6, с.105-109.

• +Белых В.Н. Элементарное введение в качественную теорию и теорию бифуркаций динамических систем. // Соросовский образовательный журнал. 1997, №1, с.115-121.

• Бронштейн Е.М. Новое о квадратном трехчлене. // Соросовский образовательный журнал. 1999, №9, с.123-127.

• Гукенхеймер Дж., Холмс Ф.

• Дьяконов В.П. MATLAB 7.*/R2006/R2007: Самоучитель. – М.: ДМК Пресс, 2008. – 768 с.: ил. (MATLAB 7.R22. Самоучитель.pdf)

• Малинецкий Г.Г. Хаос. Тупики, парадоксы, надежды. Компьютера, 1998, №47.

• Малинецкий Г.Г., Курдюмов С.П.. Нелинейная динамика и проблемы прогноза. Вестник РАН. 2001, т.71, №3, с.210-232.

• Маневич Л.И. О теории катастроф. // Соросовский образовательный журнал. 2000, №7, с.85-90.

• Медведева Н.Б. Динамика логистической функции. // Соросовский образовательный журнал. 2000, №8, с.121-127.

• Трубецков Д.И. Турбулентность и детерминированный хаос. Соросовский образовательный журнал. 1998, №1, с.77-83.

• Фейгин М.И. Особенности поведения динамических систем в окрестности опасных бифуркационных границ // Соросовский образовательный журнал. 1999, №7, с.122-127.

• Фейгин М.И. Динамические системы, функционирующие в сопровождении опасных бифуркаций. // Соросовский образовательный журнал. 1999, №10, с.122-127.

• Шредер М. Фракталы, хаос, степенные законы. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2005, 528 с. (с. 348-353)

• Эйдельман Е.Д. Конвективные ячейки: три приближения теории опытов Бенара. // Соросовский образовательный журнал. 2000, №5, с.94-100.

• Li T.-Y., Yorke J.A. Period three implies chaos.// Amer.MathMonthly. 1975, v.82, pp.982-958.

• Yang S.-K., Chen C.-L., Yau H.-T. Control of chaos in Lorenz system. // Chaos, Solitons and Fractals. 2002, v.13, pp.767-780.

• Zhou T., Chen G., Tang Y. A universal unfolding of the Lorenz system. // Chaos, Solitons and Fractals. 2004, v.20, pp.979-993.