Результаты численного исследования, сравнение с экспериментом.
В настоящей работе представлены результаты экспериментального и численного исследования скорости одиночного сферического пузырька воздуха при всплытии в вязкой жидкости при малых числах Рейнольдса с учетом нестационарных эффектов. В отличие от известных работ исследован режим движения при малых числах Рейнольдса (Re<1).
Плотность раствора варьировалась в диапазоне 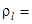 (935÷960) кг/м3. Вязкость раствора изменялась в пределах 0.2÷1.1 Па·с. Диаметр пузыря находился в диапазоне (
(935÷960) кг/м3. Вязкость раствора изменялась в пределах 0.2÷1.1 Па·с. Диаметр пузыря находился в диапазоне ( 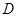 =(2÷5.5) мм.
=(2÷5.5) мм.
Не смотря на то, что для скорости всплытия пузыря получены аналитические решения, их вычисление невозможно без применения компьютерного моделирования, поскольку они очень громоздки и содержат интеграл ошибок. В связи с этим была написана и отлажена программа на алгоритмическом языке Fortran, реализующая алгоритм расчета.
Для планирования эксперимента были проведены параметрические расчеты при различных значениях коэффициента динамической вязкости и размерах воздушного пузыря. Ставилась задача найти рабочую область в плоскости ( 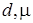 ), в которой выполняется условие Re<1.
), в которой выполняется условие Re<1.
Были проведены параметрические расчеты для определения рабочей области Re<1. На рис. 1 приведены результаты расчетов для 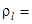 935 кг/м3.
935 кг/м3.
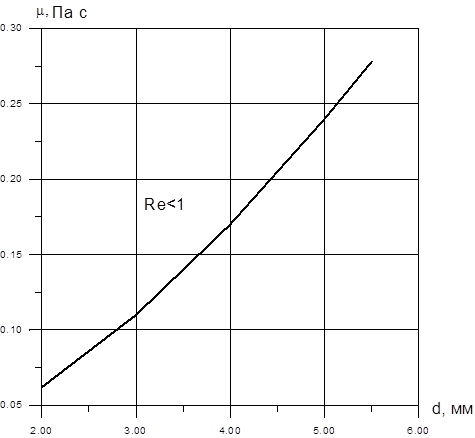
Рис. 1. Рабочая область для случая 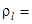 935 кг/м3
935 кг/м3
Любая точка с координатами ( 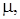 d), находящаяся выше кривой (Re=1) попадает в рабочую область Re<1. Для того, чтобы увидеть, как зависит скорость всплытия пузырька от диаметра пузыря, были проведены расчеты для рабочей жидкости (это смесь касторового масла с водой) с плотностью
d), находящаяся выше кривой (Re=1) попадает в рабочую область Re<1. Для того, чтобы увидеть, как зависит скорость всплытия пузырька от диаметра пузыря, были проведены расчеты для рабочей жидкости (это смесь касторового масла с водой) с плотностью 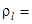 935 кг/м3 с различными размерами пузыря с фиксированным значением коэффициента динамической вязкости
935 кг/м3 с различными размерами пузыря с фиксированным значением коэффициента динамической вязкости 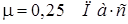 . Результаты показаны на рис. 2
. Результаты показаны на рис. 2
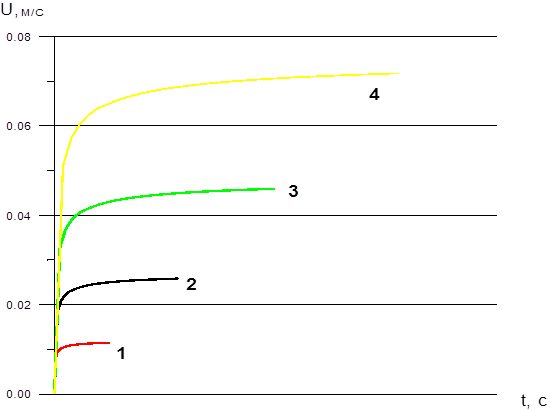
Рис 2 Зависимость скорости всплытия пузыря от диаметра пузыря. 1– d=2 мм, 2–d=3 мм, 3–d=4 мм, 4–d=5 мм
Из рисунка видно, чем больше диаметр пузыря, тем больше его скорость и тем меньше ему понадобится времени для всплытия.
Для того, чтобы увидеть, как зависит скорость всплытия пузырька от вязкости жидкости, были проведены расчеты с различными значениями коэффициента динамической вязкости 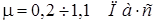 и фиксированным размером пузыря d=3 мм. Результаты показаны на рис. 3.
и фиксированным размером пузыря d=3 мм. Результаты показаны на рис. 3.
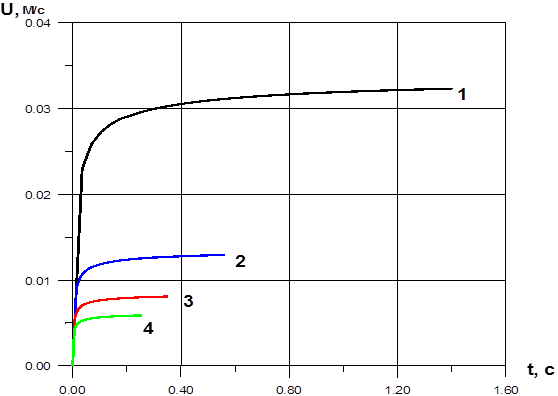 |
Рис 3. Зависимость скорости всплытия пузыря от вязкости жидкости. 1– 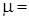 0.2;
0.2;
2– 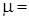 0.5; 3–
0.5; 3– 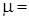 0.8; 4–
0.8; 4– 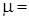 1.1;
1.1;
Из рисунка видно, что чем больше вязкость жидкости, тем меньше скорость всплытия.
При проведении экспериментов на кинокамеру фиксировалась только высота всплытия и текущее время. Скорость вычислялась численным дифференцированием по формуле 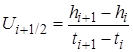 . В связи с этим ниже приведены полученные из расчетов зависимости высоты всплытия от времени для тех же вариантов.
. В связи с этим ниже приведены полученные из расчетов зависимости высоты всплытия от времени для тех же вариантов.
На рис. 4, 5 приведены результаты расчетов.
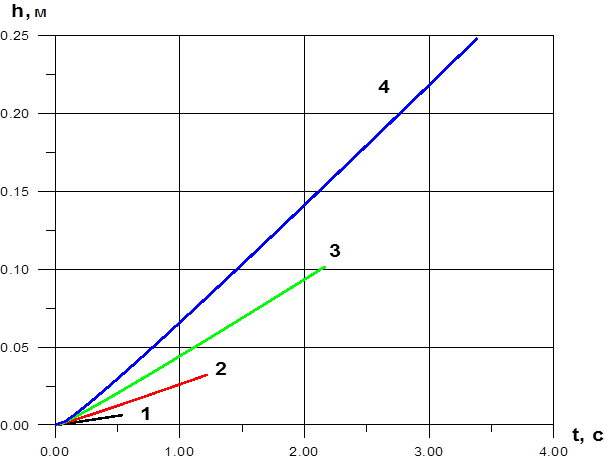
Рис 4. Зависимость высоты всплытия пузыря от времени; 1– d=2 мм, 2–d=3 мм, 3–d=4 мм, 4–d=5 мм
Видно, что для большего диаметра пузыря высота всплытия больше. Это объясняется тем, что сила Архимеда является превалирующей.
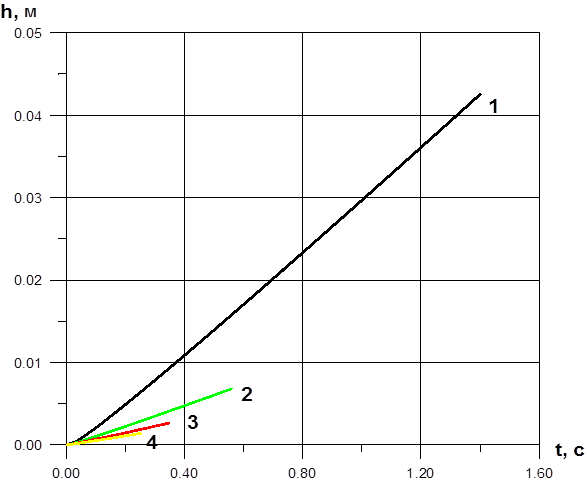 Рис 5. Зависимость высоты всплытия пузыря от времени диаметром 3 мм при различных значениях коэффициента динамической вязкости. 1–
Рис 5. Зависимость высоты всплытия пузыря от времени диаметром 3 мм при различных значениях коэффициента динамической вязкости. 1– 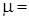 0.2; 2–
0.2; 2– 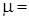 0.5; 3–
0.5; 3– 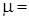 0.8; 4–
0.8; 4– 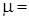 1.1;
1.1;
Как и следовало ожидать, высота всплытия в одно и то же время выше в менее вязкой жидкости. Характер изменения высоты от времени для обоих случаев (рис. 4, 5) одинаков. В первые моменты времени (когда скорость пузыря быстро возрастает) зависимость нелинейная, а дальше видим практически прямую.
Был проведен эксперимент по измерению высоты всплытия и скорости пузыря воздуха диаметром d=3,2 мм в жидкости плотностью 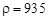 кг/м3, с коэффициентом динамической вязкости
кг/м3, с коэффициентом динамической вязкости 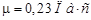 . Ниже в таблицах 1 и 2 и на рисунках 6, 7 приведены результаты.
. Ниже в таблицах 1 и 2 и на рисунках 6, 7 приведены результаты.
Таблица 1
Зависимость высоты всплытия пузырька от времени. Результаты эксперимента.
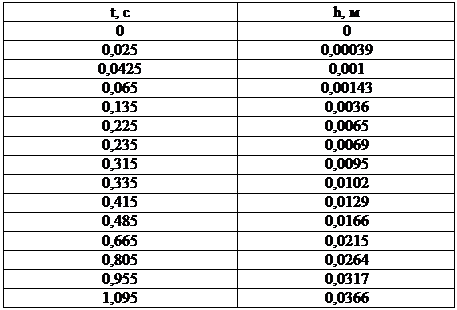
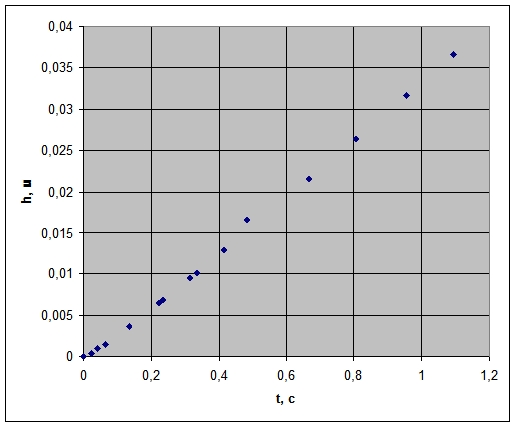
Рис. 6. Зависимость высоты всплытия пузырька от времени. Результаты эксперимента.
Таблица 2
Зависимость скорости пузырька от времени. Результаты эксперимента.
| t, c | U, м/c |
| 0,025 | 0,0175 |
| 0,0425 | 0,024 |
| 0,1 | 0,0306 |
| 0,225 | 0,0337 |
| 0,235 | 0,0347 |
| 0,315 | 0,035 |
| 0,335 | 0,033 |
| 0,415 | 0,033 |
| 0,485 | 0,034 |
| 0,665 | 0,035 |
| 0,805 | 0,035 |
| 0,955 | 0,0355 |
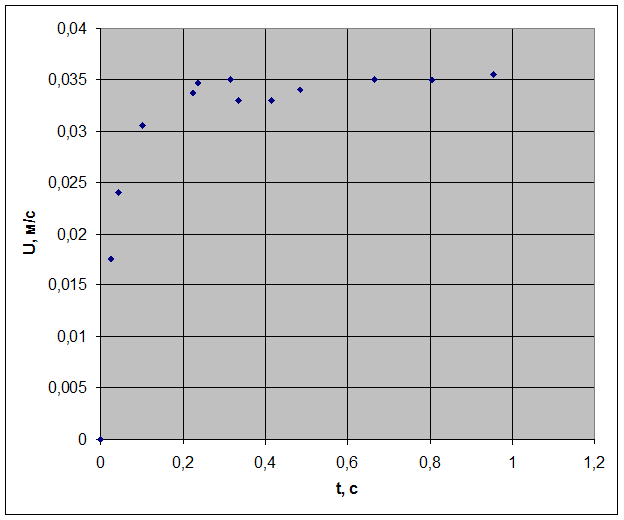
Рис. 7. Зависимость скорости пузырька от времени. Результаты эксперимента.
Для сравнения с экспериментом были проведены расчеты для тех же условий. Использовались две математические модели: с учетом присутствия в жидкости поверхностно–активных добавок (ПАВ) и без ПАВ с учетом поправки Адамара. Эксперимент проводился без использования ПАВ. На рис. 8 приведено сравнение результатов расчетов с результатами проведенных экспериментов.
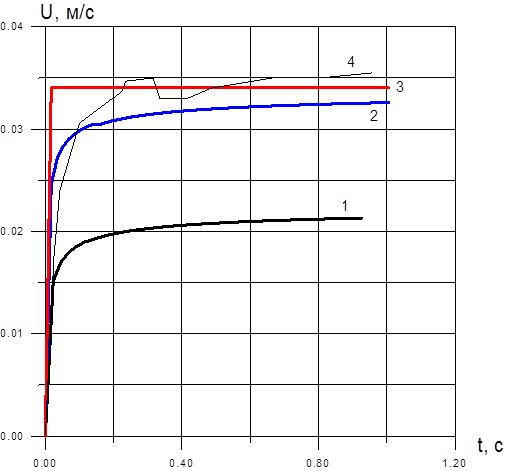
Рис. 8. Зависимость скорости всплытия пузыря от времени. 1–без поправки Адамара; 2–с поправкой Адамара; 3–коэффициент сопротивления по Стоксу без учета силы Басе и присоединенной массы
Из рис. 8 видно, что величина скорости всплытия пузыря при учете поправки Адамара достаточно хорошо коррелирует с результатами эксперимента (особенно при малых временах, когда нестационарность движения велика).
Из результатов, приведенных на рис. 8 можно сделать вывод о том, что влияние наследственной силы Бассе значительно. На начальном участке (для t<0,1 c) наблюдается хорошее совпадение с экспериментом, далее отличие порядка 10%. Различие результатов с одной стороны можно объяснить тем, что Стокс вывел выражение для коэффициента сопротивления для Re<0.1 (что выполняется на начальном участке); с другой стороны это объясняется погрешностью эксперимента. На рис. 9 приведено сравнение результатов расчета с экспериментом по высоте всплытия пузыря.
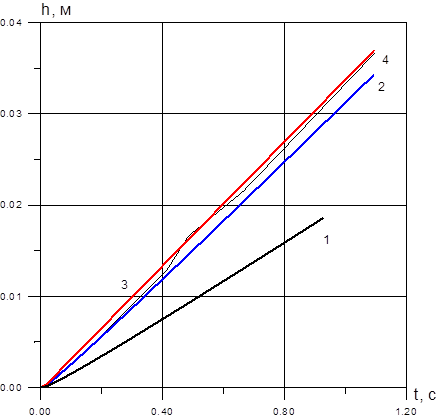
Рис. 9. Зависимость высоты всплытия пузыря от времени. 1–без поправки Адамара; 2–с поправкой Адамара; 3–коэффициент сопротивления по Стоксу без учета силы Бассе и присоединенной массы; 4–результаты эксперимента
Анализируя результаты, приведенные на рис. 9, видим, что в самом начале всплытия (до 0,4 с) наилучшее приближение дает расчетная модель с учетом поправки Адамара в коэффициенте сопротивления.
На рис. 10 приведено распределение сил, действующих на пузырь диаметром 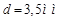 . Вязкость жидкости
. Вязкость жидкости 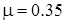 Па с,
Па с, 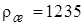 кг/м3. В коэффициенте сопротивления использована поправка Адамара–Рыбчинского.
кг/м3. В коэффициенте сопротивления использована поправка Адамара–Рыбчинского.
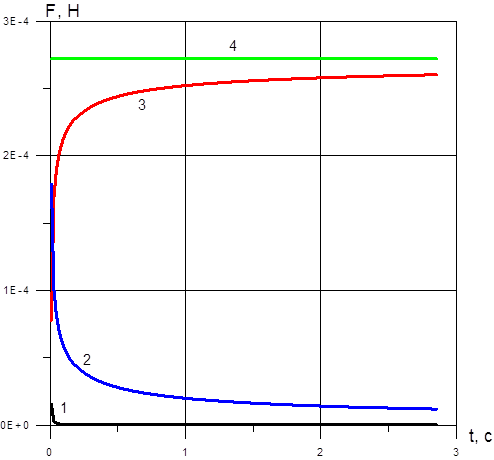
Рис. 10. Изменение во времени сил, действующих на пузырь; 1–сила инерции (присоединенной массы); 2–сила Бассе; 3–сила сопротивления; 4–сила Архимеда. Все силы даны по абсолютной величине, все они, кроме силы Архимеда отрицательны.
Из рисунка видно, что наибольшей по абсолютной величине является сила Архимеда. Сила сопротивления возрастает при увеличении скорости пузыря и приближается асимптотически к силе Архимеда. При больших временах (когда сила Бассе и сила, связанная с присоединенной массой, обратятся в ноль) сила сопротивления достигнет величины силы Архимеда и скорость пузыря перестанет изменяться (достигается выход на стационарный режим движения). Сила Бассе и сила, связанная с присоединенной массой с течением времени очень быстро уменьшаются, что говорит об уменьшении степени нестационарности процесса всплытия пузыря.
Видно, что эффект присоединенной массы влияет на движение пузыря значительно меньшее время (<0,1 c), чем сила Бассе.
Выводы
1. Создана программа расчета скорости и высоты всплытия пузыря с учетом силы Бассе и эффекта присоединенной массы при Re<1 на алгоритмическом языке Fortran.
2. Сравнение с результатами эксперимента показало хорошее совпадение расчетных и опытных данных.
3. Численные исследования, проведенные по этой программе, позволили грамотно спланировать условия эксперимента.
4. Полученные результаты показывают важность учета силы Бассе и эффекта присоединенной массы в нестационарных процессах.
Литература
1. Clift R., Grase J.R., Weber M.E. Bubbles, drops and particles. New York : Academic Press. 1978. 369 р.
2. Нигматулин Р.И.
3. Basset A.B. Treatise on hydrodynamics. London: Deighton Bell, 1888. Vol. 2. Chap. 22. P. 285-297.
4. Boussinesq J. Theorie Analytique de la chaleur. Paris, 1903. Vol.2. 224 p.
5. Oseen C.W. Hydrodynamik. Leipzig, 1927. 132 p.
6. Soo S.L. Fluid dynamics of multiphase systems. Braisdell, Waltham, MA, 1967.
7. M.X. Maxey, J.J. Riley. Equation of motion for small rigid sphere in a nonuniform flow // Phys. Fluids. 1983. №26. P. 883-889.
8. Michaelides E.E.A novel way of computing the Basset term in unsteady multiphase flow computations // Physics of fluids, A1. 1992. V. 4, № 7.Р. 1579-1582.
9. Невский Ю.А., Осипцов А.Н. О роли нестационарных и «наследственных» сил в задачах гравитационной конвекции суспензий // Вестник Московского университета. Серия 1. Математика. Механика. 2008. № 4. С. 37-40.
10. Dorgan A.J., Loth E. Efficient calculation of the history force at finite Reynolds numbers // International Journal of Multiphase Flow. 2007. Vol. 33. P.833-848.
11. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.6. Гидродинамика. М.:Наука, 1986. 736 с.
12. Ramarao B.V., Tien Chi. Role of Basset force on particle deposition in stagnation flow // J. Aerosol Sci. Vol.21, № 5. Р. 597-611.
13. A.S. Sangani, D.Z. Zhang, A. Prosperetti. The added mass, Basset, and viscous drag coefficients in nondilute bubbly liquids undergoing smallamplitude oscillatory motion // Phys. Fluids A 3 (12). 1991. P.2955-2970.
14. Thomas P.J. On the influence of the Basset history on the motion of a particle through a fluid // Physics of fluids А4. 1992. Р.2090-2093.
15. Druzhinin O.A., Ostrovsky L.A. The influence of Basset force on particle dynamics in two-dimensional flows // Physica D. 1994. № 76. P. 34-43.
16. Mordant N., Pinton J.-F. Velocity measurement of a settling sphere // The European Physical Journal B. 2000. № 18. P.343-352.
17. Jian Zhang, Liang-Shih Fan. On the rise velocity of an interactive bubble in liquids // Chemical Engineering Journal. 2003. Vol. 92. P. 169-176.
18. Mustapha Abbad, Mohamed Souhar. Effects of the history force on an oscillating rigid sphere at low Reynolds number // Experiments in Fluids. 2004. № 36. Р. 775-782.
19. Sobral Y.D., Olivera T.F., Cunha F.R. On the unsteady forces during the motion of a sedimenting particle // Powder Technology, 2007. V. 178, № 2. P. 129-141.
20. Dorgan A.J., Loth E. Efficient calculation of the history force at finite Reynolds numbers // International Journal of Multiphase Flow. 2007. Vol. 33. P.833-848.
21. Li Zhang, Chao Yang, Zai-Sha Mao. Unsteady motion of a single bubble in highly viscous liquid and empirical correlation of drag coefficient // Chemical Engineering Science. 2008. № 63. Р. 2099-2106.
22. Водопьянов И.С., Петров А.Г., Шундерюк М.М. О нестационарном осаждении сферической твердой частицы в вязкой жидкости // Механика жидкости и газа. 2010. № 2. С. 98-107.
23. Голованчиков А.Б., Балашов В.А., Меренцов Н.А. Моделирование нестационарного падения сферической капли в поле силы тяжести //Известия ВолГТУ. 2012. Т. 4, № 13. С. 8-12.
24. Лабунцов Д.А., Ягов В.В. Механика двухфазных систем. М.: Издательство МЭИ. 2000. 374 с.
25. Park W.C., Klausner J.F., Mei R. Unsteady forces on spherical bubbles // Experiments in fluids. 1995. Vol.19. P. 167-172.
26. Лойцянский Л.Г. Механика жидкости и газ. М.: Наука, 1987. – с.428-429
27. Миньков, С. Л. Информационные технологии и компьютерное моделирование. учебное пособие / А. С. Ткаченко, В. М. Ушаков. – Изд-во ТГПУ. – 2005.- 269 с.
28. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.6. Гидродинамика. М.:Наука, 1986. 736 с.
29. Васенин И.М., Ткаченко А.С., Усанина А.С. Влияние силы Бассе на всплытие пузырька в вязкой жидкости // Материалы VIII всероссийской научной конференции «Фундаментальные и прикладные проблемы современной механики». – Томск: Изд-во ТГУ. – 2013. (в печати).
30. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. 4-е изд., перераб. и доп. М.: Наука. Гл. ред. физ. -мат. лит. 1973. -749 с
ПРИЛОЖЕНИЕ
П.1. Программа расчета
program basse !CD по Адамару-Рыбчинскому сила Бассе как в классическом решении Васенина
!члены exp*erf логарифмируются, а потом потенцируются, чтобы избежать переполнения. Расчет возможен
! для mu=0.35 и ds=0.005 до времени 12 секунд, далее erf уходит в ноль
! !Zadatscha dla puzira !!!!!!!!!!!!!!
double precision b,c,T0,h,t,ds,ros,mu, A,TT,u1,u2,uu,ust1,ust2,x,xst,y1,y2,fi,kk,upr,bb,ustarh,fiadam
integer*4 n,lam,ksi
real g,b1,b2,Tk
common /aa/b1,b2,b3,g,Tk
open(1,file="adamar.dat")
b1=(3.0*sqrt(1.5)+sqrt(19.0)/2.0)/2.0
b2=(3.0*sqrt(1.5)-sqrt(19.0)/2.0)/2.0
b3=8.0*sqrt(19.0)/35.0
g=9.81
NN=160
Tk=1600.0 !-это 12 секунд !конечное время расчета безразмерное
mu=0.23 !!вязкость касторового масла !1.5 !вязкость водно-глицеринового раствора: 0.4-для концентрации 91,308,здесь вода
ros=935 !960.0 ! это касторка 1235.4 !плотность водно-глицеринового раствора для той же концентрации (чистая вода)
rok=1.25 ! плотность воздуха в пузырьке
ds=0.0032 !37 !0.01 !диаметр капли
T0=ros*ds*ds/(24*mu) !характерное время
lam=0
ksi=1
h=Tk/NN !шаг по времени безразмерный, N-количество шагов
t=0.0 !текущее безразмерное время
n=0
u1=0.0
ust1=0.0
x=0.0
xst=0.0
A=0.0
TT=0.0
fi=18.0*mu/(rok*ds*ds)
fiadam=2.0/3.0*fi
kk=1.0+ros/(2.0*rok)
bb=b1
b=Tk
! c=Erf(1000000, bb*10.2D+0, b)
! c=770.0
! b=dexp(c)
do while (n .le. NN)
! TT=n*h ! T(n)=t/T0
t=TT
! A(n)=a(T0,t)
u2=ub(T0,t) !скорость с учетом силы Бассе и присоединенной массы
! b=uu
ust2=2.0*g*T0*(1-dexp(-TT)) !Скорость по Стоксу
ustarh=g/fiadam*(1-ros/rok)*(1-dexp(-fiadam*t*T0))
x=x+T0*(u1+u2)*h/2
! c=x(n)
xst=xst+T0*(ust1+ust2)*h/2
if(n.eq.lam)then
lam=lam+ksi
! write(*,*) 'Upr=', g/fi*(1.0-1.0/ros)*(1-dexp(-fi/kk*T0*TT))
write(*,*) ' T=',T0*TT,' u=',u2,' ust=',ust2,' Re=',ds*u1*ros/mu,'T(n)=',TT,'x=',x
endif
y1=b1*dsqrt(t)
y2=b2*dsqrt(t)
write(1,1) TT*T0,u2, ust2,x,xst,TT,n !,y1,y2,Erf(1000000,y1,Tk),Erf(1000000,y2,Tk)
u1=u2
ust1=ust2
TT=TT+h
n=n+1
enddo
close(1)
1 format(7f20.11,i7,4e12.5)
end
double precision function ub(T0,t)
double precision T0,t
integer*4 num
double precision Xmax,a,a1,c,d
common /aa/b1,b2,b3,g,Tk
num=5000000 !500000 !40000
Xmax=Tk; !5056.0 !78000.0 !51200 !25600 !6400.0 !40
c=Erf(num,b2*dsqrt(t),Xmax)
d=dexp(b2*b2*t+dlog(c))
a=1.0/b2*d
c=Erf(num,b1*dsqrt(t),Xmax)
if (dabs(c).gt.0.0) then
d=dexp(b1*b1*t+dlog(c))
else
d=0.0
endif
a1=1.0/b1*d
a=(a-a1)/b3
! a=(1.0/b2*exp(b2*b2*t)*Erf(num,b2*dsqrt(t),Xmax)-1.0/b1*exp(b1*b1*t)*Erf(num,b1*dsqrt(t),Xmax))/dsqrt(5.0)
ub=2.0*g*T0*(1.0-a)
end
double precision function Erf(num, arg, Xmax)
integer*4 num
double precision arg, Xmax
integer*4 k
double precision x,asch,kvadrat,kvadra,kvadrm,exponent,expa,expm,nul,sum,fpi
! fpi=1.128379167095 !5125738961589
fpi=2.0/dsqrt(dacos(-1.0D+0))
asch=(Xmax-arg)/num
kvadra=-arg*arg
expa=dexp(kvadra)
kvadrm=-Xmax*Xmax
expm=dexp(kvadrm)
nul=(expa+expm)*asch/2
k=0
sum=0.0
x=arg
do while(k.lt.num)
x=x+asch
kvadrat=-x*x
exponent=dexp(kvadrat)
sum=sum+exponent
k=k+1
enddo
sum=sum*asch
sum=sum+nul
Erf=(FPI*sum)
end
