Математическое ожидание дискретной случайной величины

Глава 6.

Числовые характеристики случайных величин

Математическое ожидание и его свойства

Для решения многих практических задач не всегда требуется знание всех возможных значений случайной величины и их вероятностей. Более того, иногда закон распределения исследуемой случайной величины просто неизвестен. Однако требуется выделить какие-то особенности этой случайной величины, иначе говоря, числовые характеристики.

Числовые характеристики – это некоторые числа, характеризующие те или иные свойства, отличительные признаки случайной величины.

Например, среднее значение случайной величины, средний разброс всех значений случайной величины вокруг своего среднего и т.д. Главное назначение числовых характеристик состоит в том, чтобы в сжатой форме выразить наиболее важные особенности распределения исследуемой случайной величины. Числовые характеристики в теории вероятностей играют огромную роль. Они помогают решать, даже без знания законов распределения, очень многие важные практические задачи.

Среди всех числовых характеристик, в первую очередь выделим характеристики положения.Это характеристики, которые фиксируют положение случайной величины на числовой оси, т.е. некое среднее значение, около которого группируются остальные значения случайной величины.

Из характеристик положения наибольшую роль в теории вероятностей играет математическое ожидание.

Математическое ожидание иногда называют просто средним значением случайной величины. Оно является неким центром распределения.

Математическое ожидание дискретной случайной величины

Рассмотрим понятие математического ожидания вначале для дискретной случайной величины.

Прежде чем вводить формальное определение, решим следующую простую задачу.

Пример 6.1. Пусть некий стрелок производит 100 выстрелов по мишени. В результате получена следующая картина: 50 выстрелов – попадание в "восьмерку", 20 выстрелов – попадание в "девятку" и 30 – в "десятку". Какова средняя сумма очков при одном выстреле.

Решение данной задачи очевидно и сводится к нахождению среднего значения 100 чисел, а именно, 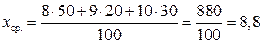очков.

Преобразуем дробь, почленно поделив числитель на знаменатель, и представим среднее значение в виде следующей формулы:

. ■

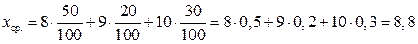Предположим теперь, что число очков при одном выстреле – это значения некоторой дискретной случайной величины Х. Из условия задачи ясно, что х₁=8; х₂=9; х₃=10. Известны относительные частоты появления этих значений, которые, как известно, при большом числе испытаний приближенно равны вероятностям соответствующих значений, т.е. р₁≈0,5; р₂≈0,2; р₃≈0,3. Итак, 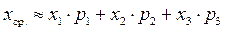. Величина в правой части – это математическое ожидание дискретной случайной величины.

Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее возможных значений на вероятности этих значений.

Пусть дискретная случайная величина Х задана своим рядом распределения:

Х	х1	х2	…	хn
Р	р1	р2	…	рn

Тогда математическое ожидание М(Х) дискретной случайной величины определяется по следующей формуле:

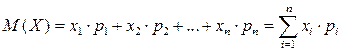(6.1)

Если дискретная случайная величина принимает бесконечное счетное множество значений, то математическое ожидание выражается формулой:

,

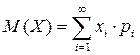причем математическое ожидание существует, если ряд в правой части равенства абсолютно сходится.

Пример 6.2. Найти математическое ожидание выигрыша Х в условиях примера 5.1.

Решение. Напомним, что ряд распределения Х имеет следующий вид:

Х
Р	0,7	0,2	0,1

Получим М(Х)=0∙0,7+10∙0,2+50∙0,1=7. Очевидно, что 7 рублей – это справедливая цена билета в данной лотерее, без различных затрат, например, связанных с распространением или изготовлением билетов. ■

Пример 6.3. Пусть случайная величина Х – это число появлений некоторого события А в одном испытании. Вероятность этого события равна р. Найти М(Х).

Решение. Очевидно, что возможные значения случайной величины: х₁=0 – событие А не появилось и х₂=1 – событие А появилось. Ряд распределения имеет вид:

Х
Р	1−р	р

Тогда М(Х) = 0∙(1−р)+1∙р = р. ■

Итак, математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

В начале параграфа была приведена конкретная задача, где указывалась связь между математическим ожиданием и средним значением случайной величины. Поясним это в общем виде.

Пусть произведено k испытаний, в которых случайная величина Х приняла k₁ раз значение х₁; k₂ раз значение х₂ и т.д. и, наконец, k_n раз значение x_n. Очевидно, что k₁+ k₂+…+ k_n = k. Найдем среднее арифметическое 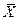всех этих значений, имеем

.

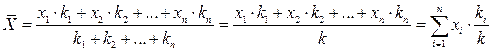Заметим, что дробь 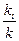- это относительная частота появления значения х_i в k испытаниях. При большом числе испытаний относительная частота приближенно равна вероятности, т.е. 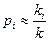. Отсюда следует, что

.

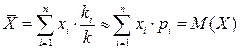Таким образом, математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины, причем тем точнее, чем больше число испытаний – в этом состоит вероятностный смысл математического ожидания.

Математическое ожидание иногда называют центромраспределения случайной величины, так как, очевидно, что возможные значения случайной величины расположены на числовой оси слева и справа от ее математического ожидания.

Перейдем теперь к понятию математического ожидания для непрерывной случайной величины.