Олебания с 2-мя степенями свободы. Нормальные колебания (моды) и нормальные частоты. Примеры.

Если система обладает несколькими степенями свободы, то при малых отклонениях от положения равновесия возможны колебания сразу по всем степеням свободы. Обычный маятник может колебаться в двух взаимно перпендикулярных вертикальных плоскостях, проходящих через точку подвеса. Поэтому он имеет две степени свободы. Наличие связи различных степеней свободы между собой придает колебанию системы со многими степенями свободы новые физические закономерности.

k

Связанной системойназывается система со многими степенями свободы, между которыми имеется связи, обеспечивающие возможность обмена энергией между различными степенями свободы. Примером связанной системы с двумя степенями свободы могут служить два маятника, соединенных между собой пружиной.

x2

	пружина		два пружинных маятника

X1 X2

Несмотря на сложность движения двух связанных маятников, оно всегда может быть представлено как суперпозиция четырех гармонических колебаний, частоты которых называются нормальными частотами связанной системы. Число нормальных частот равно числу степеней свободы. В приведенном примере имеем две степени свободы. И можно представить колебание как суперпозицию двух колебаний.

ωI S^I₁(t)=S20sin(ω_I*t+φ_I)

S^I₂(t)=S₁₀sin(ω_I*t+φ_I)

ωI, S^I20/S^I10=1 – первая мода

ωI=√(k/m)

ωII S^II₁(t)=S^II20*sin(ω_II*t+φ_II)

S^II₂(t)=S^II_10*sin(ω_II*t+φ_II)

ωII, S^II20 / S^II₁₀ = -1 – вторая мода

ωII=√((k+2k1)/m)

S₁(t)=S^I10*sin(ω_I*t+φ_I)+S^II10*sin(ω_II*t+φ_II)

S₂(t)=S^I20*sin(ω_I*t+φ_I)+S^II20*sin(ω_II*t+φ_II)

ωI,ωII, S^I20/S^I10, S^II20 / S^II₁₀ }à известны

Начальные условия S1(0), S1^'(0) S₂(0), S₂^'(0) } → S^I10 ; φ_I S^II10 ; φ_II

Если маятники отклонить одинаково в одну сторону, то они колеблются с некоторой частотой ω1, которая называется нормальной. Частота колебаний маятников, отклоненных одинаково в противоположных направлениях, является другой нормальной частотой ω2.

Если ω_I ≈ ω_II , |ω_I – ω_II | <<ω_I ≈ ω_{II ,} тогда отчетливо будут наблюдаться биения. Биение – колебание, которое происходит с медленной частотой и является суммой двух гармонических колебаний с близкими частотами. Это колебание с изменяющейся амплитудой. Оно лишь приблизительно гармоническое с частотой ω_I ≈ ω_II , а его амплитуда изменяется с частотой |ω_I – ω_II |. T_биен=2p/(ω_I – ω_{II ). Δ}ω=ω_I – ω_II <ω>=(ω_I +ω_II)/2 S₁(t)=2*S₁(t)*(cos( _Δω/2)t) *cos(<ω>t) S₂(t)=2*S₁(t)*(sin( _Δω/2)t) *cos(<ω>t).

Запас начальной кинетической и потенциальной энергий определяется из начального смещения и начальной скорости. Если бы потери энергии в системе отсутствовали, то этот начальный запас энергии оставался бы неизменным при колебаниях. Процесс колебаний сопровождался бы только переходом энергии из потенциальной в кинетическую и обратно, которые будут происходить в двое большей частотой, чем сами колебания.

U=kx² /2=kx²cos²(wt+p)/2=kX²(1+cos2(wt+p))/4;

Tk=mV²/4(1- cos2(wt+p))/4; формулы содержат двойную частоту, но изменения потенциальной и кинетической энергий происходят по гармоническому закону. Так как амплитуды смещения и скорости связаны соотношеннием V=wX; то полная энергия равна W=Tk+U=kX²/2=mV²/2;

При наличии трения , являющегося внешней силой, энергия колебаний уменьшается.

Добротноть. Для характеристики осциллирующей системы часто принимается величина Q называемая добротностью. Эта величина представляет собой умноженное на 2p отношение запасённой энергии к среднему значению энергии, теряемому за один период. Большим значениям Q соответствует слабое затухание осциллятора.Q=p/Q , где Q логарифмический декримент затухания.

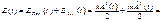
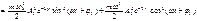
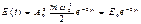
Билет № 21.

ункт 2.

Существует 2 вида волн поперечные и продольные. Если частицы распространяются со скоростью перпендикулярной скорости самой волны, то волна называется поперечной. Волна – процесс распространения энергии. Волновая поверхность – это геометрическое место точек, где частицы среды совершают одинаковые движения. По виду волновые поверхности различаются на : плоские, сферические, цилиндрические, круговые. Y(x,t)=f1(t-x/v): уравнение плоской волны бегущей вправо по оси Ox. Y(x,t)=f1(t+x/v) : уравнение плоской волны бегущей влево по оси Ox. Фронт волны– это Г. М. Т, до которых доходят возмущения к одному моменту времени Т. Плоская волна – это такая волна, фронт у которой плоский. Уравнение п. м. в. для одной точки: S*(t)=S₀sin(wt+j*) Уравнение п. б. м. в.: S(t)=S₀sin[w(t–(x/c))]

S=S(0)*cos(wt-2p*x/l)=s(0)*сos(wt-k*x) Длина волны– расстояние, на которое распространяется колебание на один период l=сТ

Скорость распространения волн – это скорость передачи энергии колебания. Частота– число полных колебаний источника в единицу времени. Фазовая скорость волны – это скорость её распространения. Ф=w(t–(x/c)) – const., w(Dt–(Dx/c))=0, (Dx/Dt)=c – фазовая скорость.S(t,x)=S₀sin[w(t–(x/c))] или S(t,x)=S₀sin[wt–kx], где k–волновое число. Волновое число:k=w/c=2p/(Tc)=2p/l; Волновой вектор: 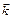= 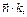где k –волновое число, n – нормаль к фронту. 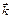={k_x; k_y; k_z;} Þ S(x, y, z, t)=S₀sin(wt–k_xx–k_yy–k_zz).

Уравнение сферической волны: S(t,r)= 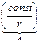cos(wt–kr), где r – радиус.

Уравнение цилиндричекой: S(t,r)= 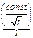cos(wt–kr), где r – радиус.

илет № 22

олновое уравнение.

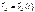S(t,r)=S₀sin(wt– 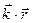); ¶²S/¶t²=–w²S; 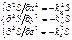Þ

¶²S/¶x²+¶²S/¶y²+¶²S/¶z²=–S(k_x²+ k_y²+k_z²)=–Sk²

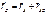¶²S/(¶t²c²)=¶²S/¶x²+¶²S/¶y²+¶²S/¶z²

¶²S/¶t²=DS/c², где DS – оператор Лапласа. c=w/k

Волновому уравнению также удовлетворяет уравнение любого импульса.

S=S(t– 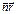/c)

Билет № 23.