Алгебраические критерии устойчивости
Наиболее распространен в инженерной практике алгебраический критерий Гурвица. Ниже приведены формулировки и методика применения критерия Гурвица.
Критерий Гурвица.
Запишем характеристическое уравнение системы n-го порядка
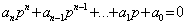 .
.
Примечание. В некоторых учебниках и задачниках по курсу ТАУ используют другую индексацию коэффициентов, а именно:
 .
.
Однако, важна не индексация коэффициентов характеристического уравнения, а соответствие каждого из них порядку производной в дифференциальном уравнении. Поэтому формально целесообразно использовать форму записи, при которой индекс коэффициента соответствует порядку производной.
Для анализа устойчивости с помощью критерия Гурвица необходимо составить матрицу коэффициентов характеристического уравнения следующего вида:
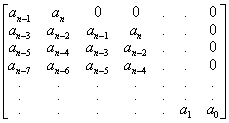 (4.10)
(4.10)
Линейная система устойчива, если при 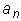 > 0 положительны все диагональные миноры матрицы коэффициентов, т.е.
> 0 положительны все диагональные миноры матрицы коэффициентов, т.е.
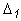 =
= 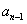 > 0
> 0
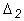 =
= 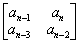 > 0
> 0
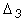 =
= 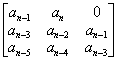 > 0
> 0
и т.д., или в общем виде
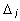 =
= 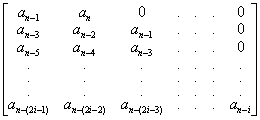 > 0, i = 1,2, ..., n (4.11)
> 0, i = 1,2, ..., n (4.11)
Если хотя бы один из определителей (4.11) отрицателен, то система неустойчива.
Так как последний столбец главного определителя 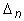 содержит всегда только один элемент
содержит всегда только один элемент 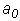 , отличный от нуля, то согласно известному свойству определителей
, отличный от нуля, то согласно известному свойству определителей
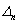 =
= 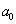
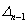 . (4.12)
. (4.12)
Если 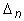 = 0, а все остальные определители положительны, то система находится на границе устойчивости. С учетом (4.12) это условие распадается на два:
= 0, а все остальные определители положительны, то система находится на границе устойчивости. С учетом (4.12) это условие распадается на два:
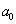 = 0 и
= 0 и 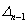 = 0. (4.13)
= 0. (4.13)
Условию 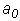 = 0 соответствует один нулевой корень, т.е. апериодическая граница устойчивости, а условию
= 0 соответствует один нулевой корень, т.е. апериодическая граница устойчивости, а условию 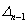 = 0 - пара мнимых корней, т.е. колебательная граница устойчивости.
= 0 - пара мнимых корней, т.е. колебательная граница устойчивости.
Совершенно очевидно, что для систем первого и второго порядка необходимым и достаточным условием устойчивости является положительность коэффициентов характеристического уравнения.
Для системы третьего порядка с характеристическим уравнением
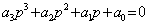
условие устойчивости
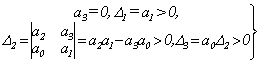 (4.14)
(4.14)
Последнее неравенство при 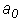 >0 эквивалентно неравенству
>0 эквивалентно неравенству 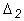 >0. Следовательно, для системы третьего порядка, кроме положительности всех коэффициентов характеристического уравнения, требуется, чтобы
>0. Следовательно, для системы третьего порядка, кроме положительности всех коэффициентов характеристического уравнения, требуется, чтобы 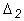 > 0.
> 0.
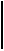 Учитывая выражение для
Учитывая выражение для 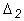 , можно сформулировать мнемоническое правило оценки устойчивости систем третьего порядка:
, можно сформулировать мнемоническое правило оценки устойчивости систем третьего порядка:
произведение средних коэффициентов характеристического уравнения должно быть больше произведения крайних.
Для устойчивости системы четвертого порядка с характеристическим уравнением
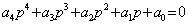 (4.15)
(4.15)
кроме положительности всех коэффициентов требуется выполнение условия
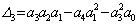 > 0. (4.16)
> 0. (4.16)
Нетрудно доказать, что при положительности всех коэффициентов условие (4.16) обеспечивает выполнение необходимого неравенства 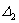 > 0.
> 0.
Таким образом,
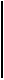 для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель
для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель 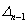 были положительными.
были положительными.
Критерий Гурвица целесообразно применять для анализа устойчивости систем не выше пятого порядка. При n>5 достаточные условия устойчивости усложняются, а вычисления определителей становится громоздким.
Пример 4.1. Определим с помощью критерия Гурвица устойчивость САУ при следующих значениях параметров:
TЯ = 0,15 c; TM = 1 c; TП = 0,01 c; KΣ = 15.
Характеристическое уравнение системы
(TП× p + 1)( TЯ TM× p2 + TM× p + 1) + KΣ = 0,
или 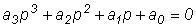 ,
,
где a3 = TП TЯ TM = 0.01× 1× 0,15 = 0,0015 c3;
a2 = TЯ TM + TП TM = 1× 0,15+ 1× 0,01 = 0,16 c2;
a1 = TM + TП = 1 + 0,01 = 1,01 c;
a0 = 1+15 = 16.
Все коэффициенты характеристического уравнения положительны, т.е. необходимое условие устойчивости выполняется. Проверим выполнение достаточного условия, для чего вычислим определитель
D2 = a1× a2 - a3× a0 = 1,01× 0,16 - 0,0015× 16 = 0,1616 - 0,0224 = +0,1376,
D2 > 0, следовательно, система устойчива.
Решим теперь обратную задачу: определим, какое максимальное значение суммарного коэффициента усиления КS допустимо по условию устойчивости.
Максимальное допустимое значение К определяется из условия нахождения системы на границе колебательной устойчивости. Это значение К называют критическим или граничным
D2 = a1× a2 - a3× a0кр = 0,
отсюда a0кр = a1× a2 /a3 = 1,01× 0,16/0,0015 = 107,73.
Ккр = a0кр - 1 = 107,73 - 1= 106,73.
Следовательно, рассмотренная в примере система устойчива, если К < Ккр.
