Решение системы линейных уравнений с помощью ранга матрицы
Пусть дана система линейных уравнений 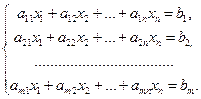 (25), коэффициенты которых принадлежат данному полю Р.
(25), коэффициенты которых принадлежат данному полю Р.
Пусть А = 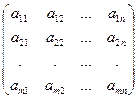 (26) матрица этой системы и А1 =
(26) матрица этой системы и А1 = 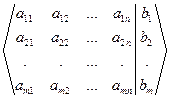 (27) расширенная матрица. Если система (25) имеет хотя бы одно решение, то её называют совместной, в противном случае система несовместная. Если все слагаемые, содержащие неизвестные, стоят в левых частях уравнений, а свободные члены – в правых частях, то система называется приведённой. Если в системе (25) хотя бы один свободный член отличен от нуля, то эта система называется неоднородной. Если же все свободные члены равны нулю, то имеем систему линейных однородных уравнений.
(27) расширенная матрица. Если система (25) имеет хотя бы одно решение, то её называют совместной, в противном случае система несовместная. Если все слагаемые, содержащие неизвестные, стоят в левых частях уравнений, а свободные члены – в правых частях, то система называется приведённой. Если в системе (25) хотя бы один свободный член отличен от нуля, то эта система называется неоднородной. Если же все свободные члены равны нулю, то имеем систему линейных однородных уравнений.
Теорема 26 (теорема Кронекера – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг её матрицы равен рангу расширенной матрицы.
Доказательство. Þ Пусть система (25) совместна. Следовательно, существуют такие элементы a1, a2, … , an , что
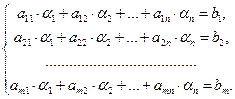
Записав эти равенства в векторной форме, получим, что в = a1×а1+ a2×а2 + … + a×аn , где а1, а2, … , аn –векторы-столбцы матрицы А, в – вектор-столбец свободных членов. Из последнего равенства следует, что системы векторов а1, а2, … , аn и а1, а2, … , аn , в эквивалентны, поэтому их ранги равны. Итак, rang A = rang A1.
Ü Пусть rang A = rang A1 = к. Не нарушая общности, можно считать, что отличный от нуля минор к-го порядка в матрице А стоит в левом верхнем углу. Векторы-столбцы обозначим а1, а2, … , ак, ак+1, … , аn, в (*). Система а1, а2, … , ак будет максимальной линейно независимой подсистемой в системе (*), следовательно, найдутся такие коэффициенты х10, х20, … , хк0, что в = х10 а1+ х20 а2+ … + хк0 ак.Это равенство равносильно равенству в = х10 а1+ х20 а2+ … + хк0 ак+ … + 0×ак+1 + … + 0×аn. Перейдя к координатам, получим:
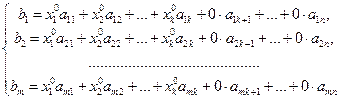 (28)
(28)
Отсюда следует, что (х10, х20, … , хк0, 0,… ,0) – решение системы (25), т.е. эта система совместна.
Из теоремы Кронекера – Капелли следуют правила решения системы линейных уравнений.
Для решения системы линейных уравнений достаточно
1. Найти ранги основной и расширенной матриц ( А и А1 ). Если rang A ¹ rang A1, то система не имеет решения.
2. Если rang A = rang A1 = к, то для решения достаточно оставить к уравнений, коэффициенты которых стоят на тех строчках матрицы А, на которых стоит базисный минор, и в этих уравнениях оставить в их левых частях те неизвестные, коэффициенты которых входят в базисный минор. Остальные неизвестные нужно перенести в правые части уравнений. Они могут принимать все возможные значения из поля Р. Эти неизвестные называются свободными. (Не нарушая общности, можно считать, что оставлены первые к уравнений и первые к неизвестных , система (29)).
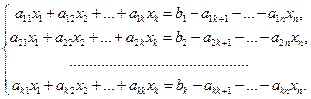 (29) (29) | Определитель левой части системы (29) отличен от нуля, число уравнений равно числу неизвестных, поэтому (по теореме Крамера) эта система при всевозможных хк+1, … , хn имеет единственное решение. |
Следовательно, неизвестные х1, х2, … , хк можно выразить через хк+1, … , хn . Формулы, с помощью которых х1, х2, … , хк выражаются через хк+1, … , хn задают так называемое общее решение данной системы уравнений. При каждом конкретном наборе переменных хк+1, … , хn мы получим единственный набор х1, х2, … , хк . Это частное решение системы уравнений. Число свободных неизвестных равно n – к. Поэтому если к = n, то свободных неизвестных нет, система (29), а поэтому и система (25), имеет единственное решение. Если же к < n, то система имеет бесконечно много решений.
Пример. Исследовать систему уравнений и решить её, если она совместна в поле R.
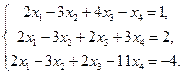
Решение. Составим матрицу и расширенную матрицу.
А1 = 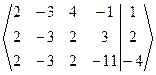 | Так как первый и второй столбцы пропорциональны, то для нахождения ранга матрицы один из них можно удалить. Будем считать, что удалён второй столбец. Минор М = 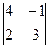 ¹ 0. ¹ 0. |
Окаймим этот минор первым столбцом и третьей строкой , получим
D = 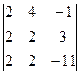 = 56 ¹ 0. = 56 ¹ 0. | Следовательно, rang A = 3. Но rang A1 не может быть больше 3. Итак, rang A = rang A1 = 3. Для решения остаются три уравнения, т.е. все уравнения. Оставим в левых частях первое, третье и четвёртое неизвестные, второе неизвестное перенесём в правые части, |
получим
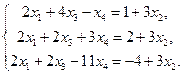 | Для этой системы D = 56, 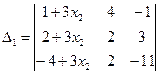 = 84х2 , = 84х2 , |
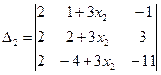 = 20,
= 20, 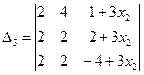 = 24. По формулам Крамера получаем х1 =
= 24. По формулам Крамера получаем х1 = 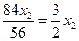 , х3 =
, х3 = 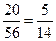 , х4 =
, х4 = 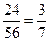 . Общее решение данной системы (
. Общее решение данной системы ( 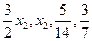 ), х2 – любое действительное число.
), х2 – любое действительное число.
