Элементов электрических систем

ГЛАВА 1

ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ СИСТЕМЫ

ЛИНЕЙНАЯ СИСТЕМА

Линейной называется система, поведение которой в определенном интервале изменения ее координат описывается совокупностью линейных уравнений (уравнений первого порядка). Несмотря на то что реально существующий объект обладает свойством линейности на ограниченном интервале изменения основных параметров, для облегчения изучения и решения физических задач приходится часто пренебрегать нелинейностью в поведении исследуемой системы. В таких случаях реальные объекты заменяются идеальными, которым приписывается свойство линейности. Допустимость такой замены полностью определяется природой изучаемой системы и требует от исследователя определенного опыта, поскольку часто такая замена может привести к значительным искажениям физической действительности.

Одним из фундаментальных свойств линейной системы является возможность представления ее выходного сигнала в виде суммы отдельных составляющих, каждая из которых может быть получена в предположении, что существует только такая составляющая. Это свойство получило название принципа суперпозиции (наложения). Совокупность упомянутых составляющих, которым свойственно порождать себе подобных на выходе линейной системы, будучи подведенным к ее входу, составляет базис собственных сигналов (функций) системы. Любой сигнал, принадлежащий базису собственных функций линейной системы, появляется на выходе системы, изменяя лишь свою амплитуду (и фазу в случае колебаний). Кроме того, действие сигнала на входе системы порождает в переходном режиме и иные составляющие, также принадлежащие базису собственных сигналов данной системы.

В случае если линейная система не изменяет своих параметров с течением времени, то основные характеристики системы не зависят от сдвига во времени. Потому такие системы называют линейными инвариантными во времени системами (ЛИВ-системами), они описываются уравнениями с постоянными коэффициентами. В этом пособии будут рассматриваться преимущественно такие системы.

ДИНАМИЧЕСКИЕ УРАВНЕНИЯ

ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ СИСТЕМ

Электрические источники энергии. Различают два вида источников: источник электродвижущей силы (ЭДС) – 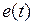(рис. 1.1, а) и источник тока – 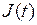(рис. 1.1, б).

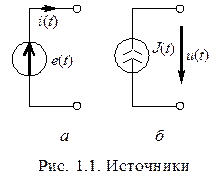В идеальном случае для первого характерна неизменность уровня напряжения, для второго – уровня тока независимо от нагрузки на зажимах. В этом случае говорят, что источники обладают бесконечной мощностью. У источника ЭДС внутреннее сопротивление равно нулю, а у источника тока – бесконечно велико. Поэтому источник ЭДС поддерживает на своих зажимах заданный уровень напряжения 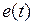независимо от значения тока 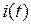, а источник тока – заданный уровень тока 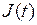независимо от напряжения .

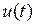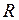Резистор (рис. 1.2) – элемент, создающий активное (с выделением тепловой энергии) сопротивление току 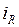. Для него справедлив закон Ома

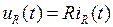. (1.1)

Выражение (1.1) представляет собой динамическое уравнение резистора. Оно может быть видоизменено

,

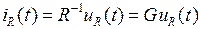где 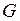– проводимость резистора.

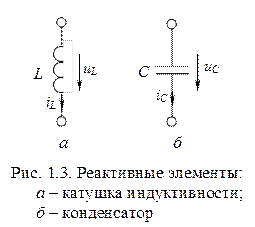
Катушка индуктивности (рис. 1.3, а) – элемент, запасающий электромагнитную энергию. Для катушки индуктивности справедлив закон Фарадея

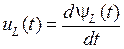. (1.2)

Учитывая, что потокосцепление 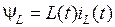, уравнение (1.2) можно записать следующим образом:

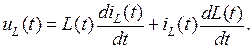
Отсюда следует, что напряжение на катушке индуктивности (в дальнейшем – просто индуктивности) создается изменением как индуктивности, так и тока во времени.

Случай с переменной индуктивностью представляет собой общий теоретический случай. Во множестве практических применений индуктивность постоянна 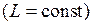, в связи с чем

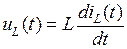. (1.3)

Уравнение (1.3) является дифференциальной формой динамического уравнения индуктивности. Используя его, можно перейти к интегральной форме уравнения

.

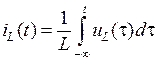Таким образом, ток индуктивности 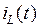определяется всей предысторией процесса. Если известно значение тока индуктивности, например, в момент времени 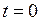, то

,

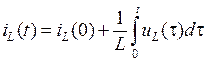где 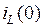– значение тока в начале отсчета времени .

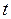Конденсатор (рис. 1.3, б) – элемент, запасающий электрическую энергию. Ток через конденсатор равен

,

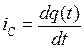где 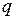– заряд конденсатора. Поскольку

,

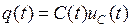то динамическое уравнение конденсатора может быть расписано более детально

.

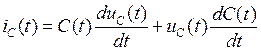Случай с изменяющейся во времени емкостью ( 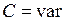) является специальным, чаще всего емкость постоянна 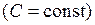. Поэтому

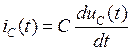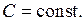, (1.4)

Уравнение (1.4) представляет собой дифференциальную форму динамического уравнения конденсатора (емкости). В интегральной форме уравнение будет следующим:

, ,

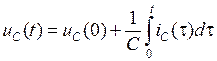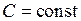где 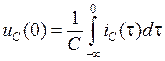– напряжение на конденсаторе в момент времени .

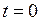1.3. АКТИВНЫЕ ЭЛЕМЕНТЫ ЧЕТЫРЕХПОЛЮСНИКОВ:

ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ

Использование операционных усилителей (ОУ) расширяет возможности синтеза электрических систем и схем различного назначения, позволяя оперировать более обобщенными схематическими понятиями. Операционный усилитель усиливает напряжение 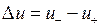, т.е. ОУ является дифференциальным усилителем, с коэффициентом усиления K

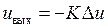. (1.5)

Для облегчения синтеза и анализа схем часто пользуются понятием идеального ОУ.

Основные свойства идеального ОУ (рис. 1.4) заключаются в следующем:

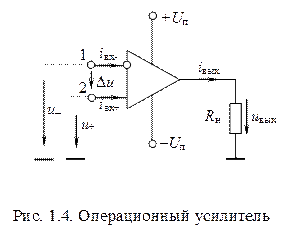а) коэффициент усиления 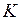стремится к бесконечности (у реальных операционных усилителей K более 10⁶);

б) выходное сопротивление стремится к нулю: 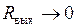. Это означает, что сигнал на выходе 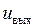поддерживается на неизменном уровне (при неизменном уровне входных сигналов) независимо от нагрузки ;

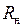в) входное сопротивление стремится к бесконечности: 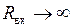. Поэтому у идеального ОУ отсутствуют входные токи: 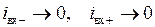(у реальных ОУ они составляют 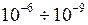А).

ПОНЯТИЕ ОБРАТНОЙ СВЯЗИ

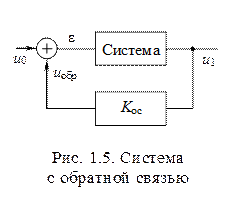
Обратной связью называется механическая или электрическая цепь, подводящая ко входу системы часть ее выходного сигнала. Например, для схемы рис. 1.5 цепь обратной связи представлена в виде усилителя

,

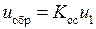где 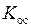– коэффициент усиления цепи обратной связи. В зависимости от того, содействует ли сигнал обратной связи 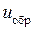повышению выходного сигнала 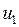или противодействует ему, говорят о положительной или отрицательной обратной связи.

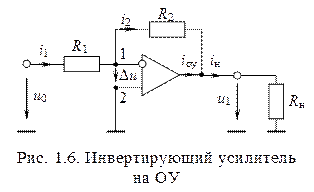
Пример 1.1. Включение ОУ по схеме инвертирующего усилителя (рис. 1.6).

Поскольку часть сигнала 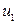с выхода ОУ через резистор 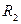подводится к инвертирующему входу, то обратная связь является отрицательной. Покажем, что под действием обратной связи разность потенциалов точек 1 и 2 в схеме поддерживаются равной нулю: 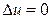. Используя обозначения рис. 1.6, получим

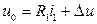, (1.6)

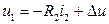. (1.7)

В силу свойства в) операционного усилителя

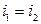. (1.8)

Решая уравнения (1.5)-(1.8) совместно, получим

.

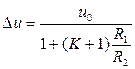Поскольку входной сигнал 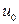ограничен, то при 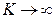разность .

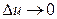Учитывая это обстоятельство, при анализе схем четырехполюсников с ОУ в дальнейшем будем исходить из предположения, что 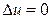. Отметим, что операционный усилитель при этом должен работать в усилительном режиме (по меньшей мере должна существовать цепь, соединяющая выход ОУ с инвертирующим входом).

Тогда из уравнений (1.6) и (1.7) следует, что

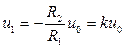. (1.9)

Здесь 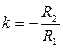– коэффициент усиления схемы. Из-за того, что он отрицательный, такое включение ОУ получило название схемы инвертирующего усилителя.

Отметим, что уровень сигнала 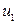, определяемого выражением (1.9), поддерживается усилителем независимо от значения резистора 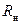за счет увеличения или уменьшения тока на выходе ОУ 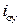, поскольку

.
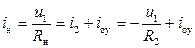