Лабораторная работа №4. «Построение парной линейной модели регрессии с использованием инструмента «Регрессия» MS EXCEL
КОНТРОЛЬНАЯ РАБОТА
на тему:
Выполнил (а)
студент (ка) курса группы __________________________
ФИО
Дата регистрации КП
на кафедре статистики и
эконометрики
Допущен(а) к защите
Руководитель:
__________________________
ученая степень, ученое звание, ФИО
Члены комиссии:
______________________ _______
ученая степень, ученое звание, ФИО подпись
______________________ _______
ученая степень, ученое звание, ФИО подпись
______________________ _______
ученая степень, ученое звание, ФИО подпись
Оценка ___________________
Дата защиты_______________
Москва, 2017
Лабораторная работа №1. Определение показателей выборочной ковариации и корреляции.
Теоретическая часть.
Взаимосвязь переменных х и у может быть выражена одним числом. Показателями взаимосвязи переменных являются их ковариация и корреляция. Ковариация определяется по одной из следующих формул
1) Cov (x,y)= 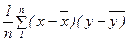
2) Cov (x, y) = 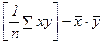
Величина показателя ковариации зависит от масштаба переменных, поэтому не является устойчивой характеристикой взаимосвязи и не подлежит смысловой интерпретации. Знак показателя ковариации указывает на направление связи: положительная величина показателя говорит о том, что связь прямая, а отрицательная – об обратной связи.
Устойчивой характеристикой взаимосвязи, то есть не зависящей от масштаба переменных, является коэффициент корреляции. В случае парной линейной зависимости переменных он определяется по формуле
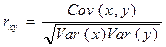
где Var (х) = 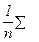 (х -
(х - 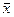 )2 и Var (y) =
)2 и Var (y) = 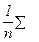 ( y -
( y - 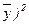
Коэффициент парной корреляции r имеет максимальное значение, равное единице, которое получается при строгой линейной положительной зависимости между выборочными значениями х и у. Аналогичным образом r принимает минимальное значение -1, когда существует линейная отрицательная зависимость. Величина r =0 показывает, что зависимость между наблюдениями х и у в выборке отсутствует. Промежуточные значения коэффициента корреляции интерпретируются следующим образом:
0 – 0,3 - слабая связь;
0,3 – 0,5 - умеренная связь;
0,5 – 0,7 - средняя сила связи;
0,7 – 1,0 - сильная или тесная зависимость.
Если на зависимую переменную у параллельно с фактором х оказывает влияние еще и фактор z, то коэффициент парной корреляции между у и х (rxy) может преувеличивать или преуменьшать действительную силу связи между ними. В таких случаях частный коэффициент корреляции является более точной мерой зависимости. Его величина определяется по формуле:
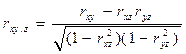 ,
,
где rху.z - коэффициент частной корреляции между х и у в случае постоянства воздействия величины z , а rху, rxz и ryz - обычные коэффициенты корреляции между х и у, между х и z, между у и z соответственно.
Квадрат коэффициента корреляции r2 называется коэффициентом детерминации, он показывает долю общей вариации зависимой переменной, объясненной влиянием независимой переменой.
Общая постановка задачи:по выборочным данным определить величину ковариации двумя способами, убедиться в равенстве результатов, сделать вывод о направлении связи переменных; изменить масштаб одной из переменных, рассчитать ковариацию по преобразованным данным, сделать выводы; по этим же данным рассчитать парный и частный коэффициенты корреляции, сделать выводы.
Список индивидуальных данных представлен в файле «исходные данные.exl» на листе «ЛПЗ №1»
Выполнение работы:
Исходные данные представлены в таблице 1.
Таблица 1. Исходные данные
| Номер торгового предприятия | Валовой доход, млн.руб. (у) | Среднегодовая стоимость основных фондов, | Среднегодовая стоимость оборотных средств, |
| млн.руб. (х) | млн. руб. (z) | ||
| Итого: | |||
| В среднем: | 111,6 | 87,9 | 59,4 |
1) Определим ковариацию.
Таблица 2. Расчет ковариации
| Год | ух | 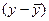 | 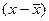 | 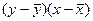 |
| 91,4 | 30,1 | 2751,14 | ||
| -48,6 | -59,9 | 2911,14 | ||
| -66,6 | -70,9 | 4721,94 | ||
| 1,4 | -37,9 | -53,06 | ||
| 9,4 | -31,9 | -299,86 | ||
| -23,6 | 14,1 | -332,76 | ||
| -1,6 | 28,1 | -44,96 | ||
| -55,6 | 36,1 | -2007,16 | ||
| -31,6 | 26,1 | -824,76 | ||
| 125,4 | 66,1 | 8288,94 | ||
| Итого: | Х | Х | 15110,6 | |
| Среднее: | 11320,7 | Х | Х | 1511,06 |
По первому способу расчета ковариации:
Cov (x,y)= 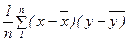 =
= 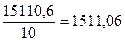 ;
;
по второму способу:
Cov (x, y) = 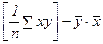 =
= 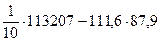 = 1511,06.
= 1511,06.
Вывод: По обеим формулам результат одинаковый, это значит, что связь есть и она является прямой.
2) Рассчитаем дисперсию переменных.
Таблица 3. Расчет дисперсии
| Год | (х-хср)2 | (y-yср)2 |
| 906,01 | 8353,96 | |
| 3588,01 | 2361,96 | |
| 5026,81 | 4435,56 | |
| 1436,41 | 1,96 | |
| 1017,61 | 88,36 | |
| 198,81 | 556,96 | |
| 789,61 | 2,56 | |
| 1303,21 | 3091,36 | |
| 681,21 | 998,56 | |
| Итого: | 4369,21 | 15725,16 |
| Среднее: | 19316,9 | 35616,4 |
3) Измерим силу связи между переменными х и у с помощью коэффициента корреляции. Рассчитаем парный коэффициент корреляции по формуле 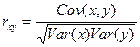 .
.
Числитель данного выражения (ковариация) определен нами ранее, а знаменатель представляет собой произведение средних квадратических отклонений взаимосвязанных признаков. Поскольку способы расчета дисперсии и среднего квадратического отклонения мы рассчитали в таблице 2, то отметим, что дисперсия переменной может быть определена с помощью программы Excel. Для этого в главном меню последовательно выберите Вставка функции / Статистические / Диспр. и заполните диалоговое окно ввода данных. В нашем примере σ2х = 1931,69 и σ2у=3561,64. Тогда
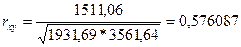
Вывод: Коэффициент корреляции говорит нам о том, что связь между показателями является средней. Коэффициент детерминации r2 (=0,331876) коэффициент детерминации показывает, что 33% влияния оказывают переменные х и y, а 67 %другие переменные.
Лабораторная работа №2. «Парный корреляционно-регрессионный анализ»
Теоретическая часть.
Форма связи между двумя экономическими переменными может быть установлена графическим методом, для этого строится коле корреляции и оценивается рассеяние наблюдений.
Параметры уравнения парной линейной регрессии 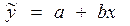 могут быть оценены методом наименьших квадратов, согласно которому:
могут быть оценены методом наименьших квадратов, согласно которому:
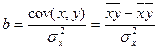 ;
;
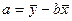 ,
,
где 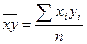 ;
;
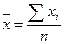 ;
;
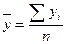 ;
;
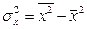 (
( 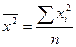 );
);
n – число наблюдений (в данном примере n= 12), i меняется от 1 до n.
Оценка тесноты связи оценивается с использованием коэффициентов корреляции ( 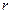 ) и детерминации (
) и детерминации ( 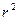 – квадрат коэффициента корреляции). Коэффициент корреляции может быть определен двумя способами:
– квадрат коэффициента корреляции). Коэффициент корреляции может быть определен двумя способами:
1) 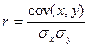 ;
;
2) 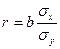 .
.
Коэффициент детерминации является показателем качества модели.
Выполнение работы:
Условие. Имеются данные по 17 регионам Российской Федерации о валовом региональном продукте (ВРП) и инвестициях в основной капитал в расчете на душу населения, представленные в виде электронной таблицы в MS EXCEL (таблица 4).
Таблица 4. Исходные данные
| № п/п | Регион | 1 вариант | |
| ВРП, тыс. руб. у | Инвестиции в основной капитал, руб.х | ||
| Центральный федеральный округ | |||
| Белгородская область | 11,4 | ||
| Брянская область | 7,6 | ||
| Владимирская область | 9,0 | ||
| Воронежская область | 9,4 | ||
| Ивановская область | 6,4 | ||
| Калужская область | 9,5 | ||
| Костромская область | 10,4 | ||
| Курская область | 10,8 | ||
| Липецкая область | 12,2 | ||
| Московская область | 11,9 | ||
| Орловская область | 9,1 | ||
| Рязанская область | 10,9 | ||
| СмоленскаяОбласть | 9,6 | ||
| Тамбовская область | 6,9 | ||
| Тверская область | 9,4 | ||
| Тульская область | 9,0 | ||
| Ярославская область | 13,6 |
Требуется построить регрессионную модель зависимости ВРП от уровня инвестиций на душу населения, рассчитать показатели тесноты связи между признаками, используя средства MS EXCEL.
1. Построим график
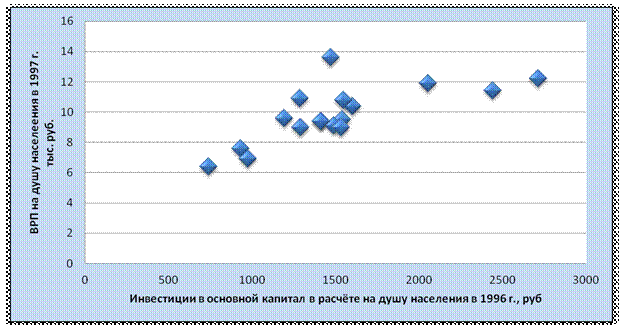
Рисунок 1. Зависимость ВРП от инвестиций в основной капитал
Вывод:Построенный график позволяет предположить, что связь между результативным и факторным признаком является линейной. В итоге получаем выборочную модель парной линейной регрессии:
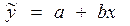
2. Найдем параметры модели методом наименьших квадратов, согласно которому:
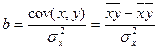 ;
;
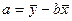 ,
,
где 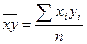 ;
;
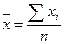 ;
;
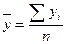 ;
;
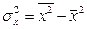 (
( 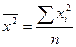 );
);
n – число наблюдений (в данном примере n= 17), i меняется от 1 до n.
Кроме того, рассчитаем 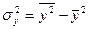 (
( 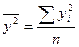 ), которая нам понадобиться в дальнейшем для определения показателей тесноты связи.
), которая нам понадобиться в дальнейшем для определения показателей тесноты связи.
Таким образом, нам необходимо рассчитать средние 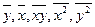 , для чего сначала нужно найти суммы
, для чего сначала нужно найти суммы 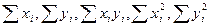 , а затем поделить каждую из них на n (таблица 2).
, а затем поделить каждую из них на n (таблица 2).
В таблице 5 средние 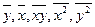 получены в 19 строке путем деления сумм в строке 18 на n= 17
получены в 19 строке путем деления сумм в строке 18 на n= 17
Таблица 5. Расчетные данные
| № п/п | Регион | 1 вариант | Х*У | у^2 | х^2 | |
| ВРП, тыс. руб. у | Инвестиции в основной капитал , руб.х | |||||
| Центральный федеральный округ | ||||||
| Белгородская область | 11,4 | 27861,6 | 130,0 | |||
| Брянская область | 7,6 | 7090,8 | 57,8 | |||
| Владимирская область | 9,0 | 81,0 | ||||
| Воронежская область | 9,4 | 13291,6 | 88,4 | |||
| Ивановская область | 6,4 | 4742,4 | 41,0 | |||
| Калужская область | 9,5 | 14639,5 | 90,3 | |||
| Костромская область | 10,4 | 16660,8 | 108,2 | |||
| Курская область | 10,8 | 116,6 | ||||
| Липецкая область | 12,2 | 148,8 | ||||
| Московская область | 11,9 | 24454,5 | 141,6 | |||
| Орловская область | 9,1 | 13568,1 | 82,8 | |||
| Рязанская область | 10,9 | 14017,4 | 118,8 | |||
| СмоленскаяОбласть | 9,6 | 11462,4 | 92,2 | |||
| Тамбовская область | 6,9 | 6734,4 | 47,6 | |||
| Тверская область | 9,4 | 13291,6 | 88,4 | |||
| Тульская область | 9,0 | 81,0 | ||||
| Ярославская область | 13,6 | 20019,2 | 185,0 | |||
| Итого | 167,1 | 25654,0 | 263131,3 | 1699,3 | 42773144,0 | |
| Среднее | 9,83 | 1509,06 | 15478,31 | 99,96 | 2516067,29 | |
| ковариация | 645,15 | |||||
| дисперсия | 3,34 | 238808,8 | ||||
| В | 0,002702 | |||||
| А | 5,75 | |||||
| R | 0,72 | 0,72 | ||||
| R^2 | 0,52 | 0,52 |
В строке 21 рассчитаны дисперсии 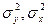 , а
, а 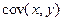 рассчитана в строке 20. В строках 22 и 23 определены параметры уравнения, в итоге получено выборочное уравнение связи:
рассчитана в строке 20. В строках 22 и 23 определены параметры уравнения, в итоге получено выборочное уравнение связи: 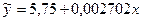 .
.
Вывод: коэффициент полной регрессии показывает, что если увеличить инвестиции на 1 рубль в расчете на душу населения, то ВРП на следующий год увеличится на 0,002702*1000=2,70 рубля.
3. Для оценки тесноты связи рассчитаем коэффициенты корреляции ( 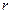 ) и детерминации (
) и детерминации ( 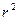 – квадрат коэффициента корреляции). Коэффициент корреляции определим двумя способами:
– квадрат коэффициента корреляции). Коэффициент корреляции определим двумя способами:
1) 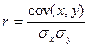 ;
;
2) 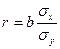 .
.
Вывод: Коэффициент корреляции, определенный двумя способами, равен 0,72. Что свидетельствует о сильной корреляционной связи между изучаемыми признаками. Коэффициент детерминации равен 0,52, вариации ВПР на душу населения зависит от факторного признака - инвестиций в основной капитал прошлого года в расчете на душу населения. Таким образом, мы подтвердили эмпирическим путем зависимость ВРП от инвестиций, т.е.52% зависит от переменной х, 48% обусловлено влиянием других переменных.
Лабораторная работа №4. «Построение парной линейной модели регрессии с использованием инструмента «Регрессия» MS EXCEL
Теоретическая часть.
Как известно из курса математической статистики нулевая гипотеза принимается, если фактическое значение критерия не превышает его критическое значение при выбранном уровне его (теоретического значения критерия) значимости. С другой стороны, если известна значимость фактического значения критерия (выводится при реализации инструмента «Регрессия» MS EXCEL), тогда статистический вывод нужно делать следующим образом:
1) задать теоретический уровень значимости 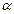 (наиболее часто применяются уровни – 1%, 5%, 0,01%)
(наиболее часто применяются уровни – 1%, 5%, 0,01%)
2) сравнить фактическую значимость 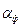 с теоретической:
с теоретической:
если 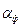 <
< 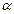 – принимается альтернативная,
– принимается альтернативная,
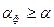 – нулевая гипотеза.
– нулевая гипотеза.
В регрессионном анализе при проверке значимости уравнения в целом или его параметров в качестве нулевой гипотезы выдвигается предположение об их недостоверности – равенстве нулю коэффициента корреляции (при оценке значимости уравнения в целом) или параметров. Следовательно, параметры или уравнение в целом будут значимы, только в том случае, если 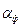 <
< 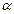 .
.
Одним из показателей качества модели является средняя ошибка аппроксимации:
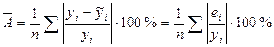 ,
,
где 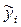 - рассчитанные по уравнению регрессии прогнозные (предсказанные значения) для каждого значения независимой переменной.
- рассчитанные по уравнению регрессии прогнозные (предсказанные значения) для каждого значения независимой переменной.
Для прогнозирования считается приемлемым уровень средней ошибки аппроксимации 8-10%.
Выполнение работы:
Требуется по исходным данным лабораторных работ №2 «Парный корреляционно-регрессионный анализ» построить уравнение линейной регрессии с использованием встроенного инструмента «Регрессия».
Таблица 6. Исходные данные
| № п/п | Регион | 1 вариант | |
| ВРП, тыс. руб. у | Инвестиции в основной капитал, руб.х | ||
| Центральный федеральный округ | |||
| Белгородская область | 11,4 | ||
| Брянская область | 7,6 | ||
| Владимирская область | 9,0 | ||
| Воронежская область | 9,4 | ||
| Ивановская область | 6,4 | ||
| Калужская область | 9,5 | ||
| Костромская область | 10,4 | ||
| Курская область | 10,8 | ||
| Липецкая область | 12,2 | ||
| Московская область | 11,9 | ||
| Орловская область | 9,1 | ||
| Рязанская область | 10,9 | ||
| СмоленскаяОбласть | 9,6 | ||
| Тамбовская область | 6,9 | ||
| Тверская область | 9,4 | ||
| Тульская область | 9,0 | ||
| Ярославская область | 13,6 |
1. Для построения модели парной линейной регрессии выберите инструмент анализа Регрессия (пункт Главного меню Сервис →Анализ данных →Регрессия) и нажмите ОК. В появившемся окне «Регрессия» щелкните флажок напротив «Входной интервал У:» и выделите соответствующий числовой диапазон данных, аналогично заполните «Входной интервал Х:», поставьте галочку «Остатки» и нажмите «ОК».
В итоге появится новый лист со следующей информацией (рисунок 2)
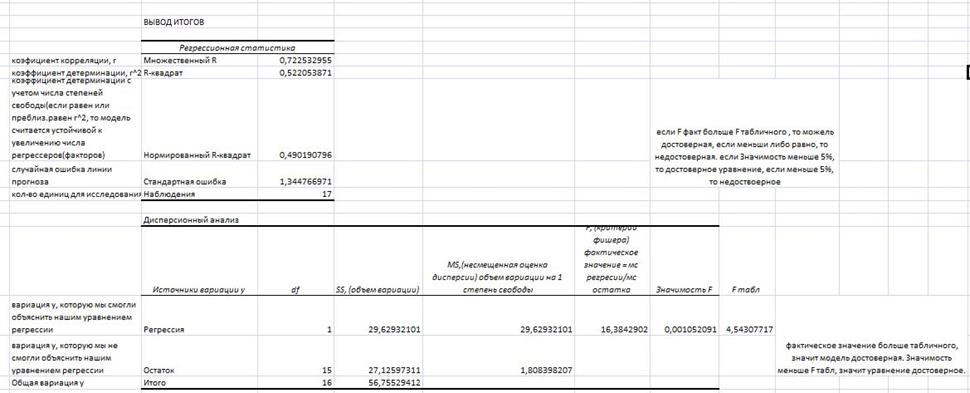 Рисунок 2
Рисунок 2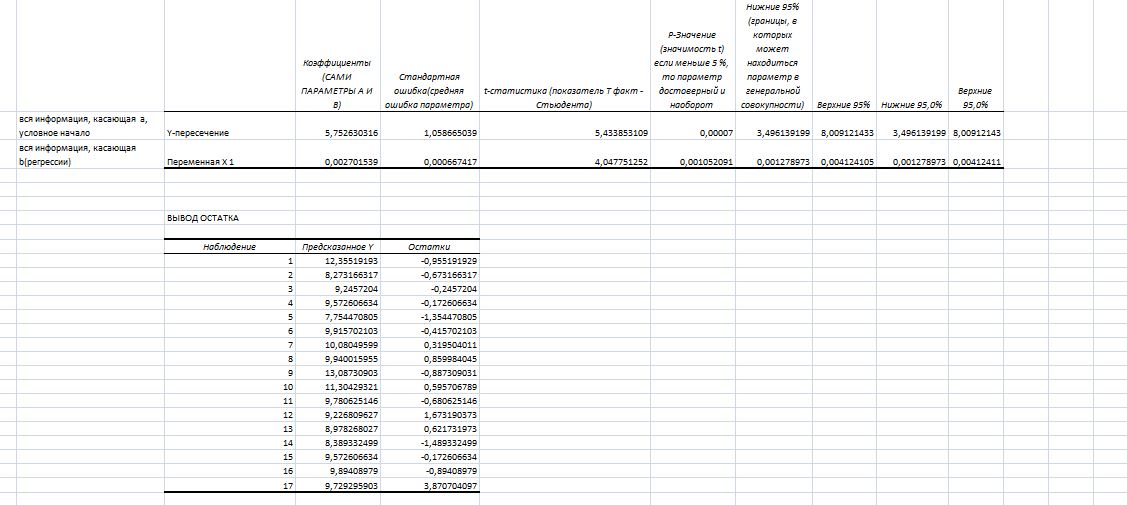 Продолжение рисунка 2
Продолжение рисунка 2
Вывод:В результате использования инструмента «Регрессия» получены те же параметры уравнения, ошибки, значения критериев F, t, получены аналогичные интервальные оценки для параметров в генеральной совокупности.
Уравнение регрессии: ỹ=5,75+0,003х. Уравнение в целом значимо F=16,38, а значимость критерия (Значимость F на листе итогов) составила 0,001*100=0,1%, что гораздо меньше обычно принимаемой 5% области (если значимость критерия находится в пределах выбранной исследователем критической области, в нашем случае 5%, то принимается альтернативная гипотеза, если больше – нулевая), следовательно, уравнение будет значимо для генеральной совокупности.
Значим параметр а: P-Значение для критерия t-Стьюдента (t-Статистика) составило 0,00007 (0,007%<5%, следовательно модель достоверная, принимается На). Коэффициент полной регрессии оказался также значимым (0,01%<5%), возможна его интерпретация: при увеличении (уменьшении) инвестиций в расчете на душу населения на 1 рубль валовой региональный продукт на душу населения увеличится (уменьшится) на 3 рубля.
Поскольку параметры выборочного уравнения регрессии значимы, то можно дать интервальную оценку параметров генерального уравнения. Нижние и верхние границы параметров на листе вывода итогов обозначены как «Нижние 95%» и «Верхние95%».
Параметр α находится в пределах от 3,49 до 8,01 : 3,49≤α ≤8,01; параметр β: 0,001≤β≤0,004 при уровне доверия данных суждений 95%.
Оценим тесноту связи между переменными. Коэффициент корреляции r=0,874, что свидетельствует о сильной тесноте связи, коэффициент детерминации позволяет сделать вывод, что 52,2% вариации ВВП связано с изменением уровня инвестиций в расчете на душу населения.
Поскольку получено значимое уравнение по критерию Фишера, с высоким коэффициентом детерминации, значимыми параметрами, то можно сделать вывод о достаточно высоком качестве модели и возможности построения прогнозов на ее основе.
Лабораторная работа №4. «Множественная линейная регрессия»
Теоретическая часть.
Множественный регрессионный анализ является развитием парного регрессионного анализа применительно к случаям, когда зависимая переменная гипотетически связана с более чем одной независимой переменной. Для двухфакторной модели выборочное уравнение множественной линейной регрессии имеет вид:
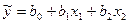 .
.
Оценка параметров осуществляется методом наименьших квадратов, который реализован в инструменте пакета анализа «Регрессия» MS EXCEL.
Коэффициенты при независимых переменных называют коэффициентами чистой регрессии, они показывают, на сколько измениться зависимая переменная, если анализируемый фактор изменится на 1 единицу своего измерения, при условии, что другие факторы останутся зафиксированными на среднем уровне.
Оценка тесноты связи в уравнении множественной регрессии, его качества проводится с использованием множественных коэффициентов детерминации и корреляции.
Стандартизованный коэффициент регрессии 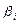 показывает, на сколько среднеквадратических отклонений
показывает, на сколько среднеквадратических отклонений 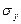 в среднем изменится зависимая переменная
в среднем изменится зависимая переменная 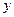 при увеличении (уменьшении) только i-той независимой переменной (другие переменные рассматриваются как неизменные, зафиксированные на своем среднем уровне), а коэффициент эластичности Эi – на сколько процентов (от средней) изменится в среднем
при увеличении (уменьшении) только i-той независимой переменной (другие переменные рассматриваются как неизменные, зафиксированные на своем среднем уровне), а коэффициент эластичности Эi – на сколько процентов (от средней) изменится в среднем 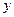 при увеличении (уменьшении) только хi.
при увеличении (уменьшении) только хi.
Выполнение работы:
Имеются данные по 17 регионам одного из федеральных округов России о валовом региональном продукте (ВРП), инвестициях в основной капитал в расчете на душу населения и уровне экономической активности населения, представленные в виде электронной таблицы в MS EXCEL (таблица 7).
Таблица 7. Исходные данные
| № п/п | Регион | 1 вариант | ||
| ВРП, млн. руб. | Инвестиции в основной капитал , тыс. руб., х1 | Уровень экономической активности населения, %, х2 | ||
| Центральный федеральный округ | ||||
| Белгородская область | 11,4 | 59,2 | ||
| Брянская область | 7,6 | 59,5 | ||
| Владимирская область | 9,0 | 63,5 | ||
| Воронежская область | 9,4 | 55,4 | ||
| Ивановская область | 6,4 | 63,7 | ||
| Калужская область | 9,5 | 65,2 | ||
| Костромская область | 10,4 | 61,0 | ||
| Курская область | 10,8 | 58,1 | ||
| Липецкая область | 12,2 | 61,9 | ||
| Московская область | 11,9 | 65,0 | ||
| Орловская область | 9,1 | 56,5 | ||
| Рязанская область | 10,9 | 58,2 | ||
| СмоленскаяОбласть | 9,6 | 60,0 | ||
| Тамбовская область | 6,9 | 55,8 | ||
| Тверская область | 9,4 | 60,7 | ||
| Тульская область | 9,0 | 59,0 | ||
| Ярославская область | 13,6 | 61,8 |
Известно, что уровень ВРП на душу населения – основной показатель уровня жизни, зависит от множества факторов. По имеющимся эмпирическим данным построим множественную модель связи уровня ВРП (у) с инвестициями в основной капитал (х1) в расчете на душу населения и уровнем экономической активности (х2). Предположим, что связь линейная:
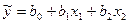 .
.
1. Построим модель с использованием инструмента «Регрессия», предусмотрев вывод остатков, в итоге получим выходные данные (рис.3).
Выборочная модель множественной линейной регрессии может быть записана в виде:


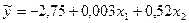 .
.
2. Оценим тесноту связи в уравнении.
EXCEL автоматически рассчитал коэффициенты множественной корреляции (множественный R) и детерминации (R-квадрат), а также скорректированный коэффициент детерминации (нормированный R-квадрат) (рис. 3).
Напомним, что коэффициент множественной детерминации определяется по формуле:

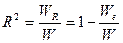 ,
,
где W – общий, 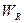 – воспроизведенный уравнением, а Wе – остаточный объем вариации.
– воспроизведенный уравнением, а Wе – остаточный объем вариации.
Множественный коэффициент корреляции (R) и скорректированный коэффициент детерминации ( 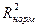 ):
):
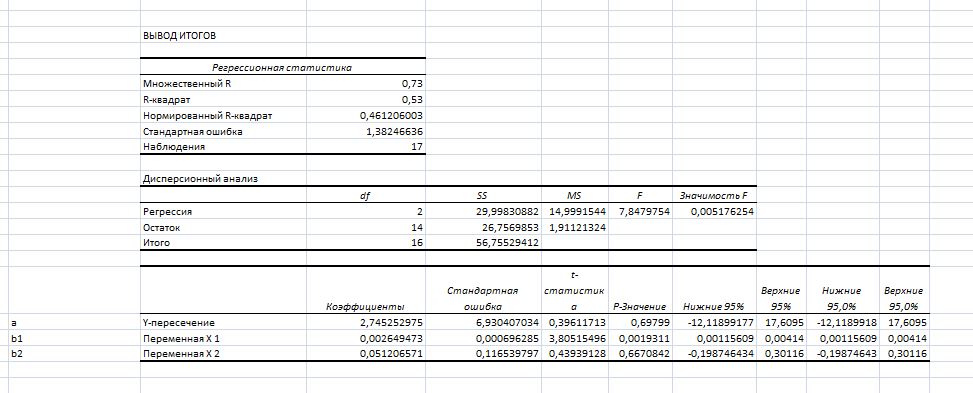 Рисунок 3. Результаты реализации инструмента «Регрессия»
Рисунок 3. Результаты реализации инструмента «Регрессия»
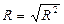 ,
,
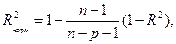
Вывод: Получили уравнение вида: у=2,75+0,003Х1+0,05Х2, где b1 показывает, если инвестиции увеличить на 1рубль, то ВРП увеличится на 2,6, если уровень эк. Активности увелится на 1 %, то ВРП увеличится на 51,2 руб.
Коэффициент корреляции равен 0,73, показывает, что связь между переменными выше средней. Коэффициент детерминации позволяет сделать вывод, что 52,9% вариации ВРП связано с изменением уровня инвестиций в расчете на душу населения. Уравнение в целом значимо F=7,85, а значимость критерия (Значимость F на листе итогов) составила 0,005*100=0,5%, что гораздо меньше обычно принимаемой 5% области (если значимость критерия находится в пределах выбранной исследователем критической области, в нашем случае 5%, то принимается альтернативная гипотеза, если больше – нулевая), следовательно, уравнение будет значимо для генеральной совокупности.
Значим параметр а: P-Значение для критерия t-Стьюдента (t-Статистика) составило 0,6999 (69,99%>5%, следовательно парметр недостоверный). Коэффициент чистой регресии b1 оказался значимым (0,2%<5%) , Коэффициент чистой регресии b2 оказался недостоверным (66,71%>5%) Поскольку получено значимое уравнение по критерию Фишера, с высоким коэффициентом детерминации, значимыми параметрами, то можно сделать вывод о достаточно высоком качестве модели и возможности построения прогнозов на ее основе.
3) Построим матрицу парных коэффициентов корреляции, оформим в таблице 8.
Таблица 8. Матрица парных коэффициентов корреляции
| Матрица парных коэффициентов корреляции | |||
| у | х1 | х2 | |
| у | |||
| х1 | 0,722532955 | ||
| х2 | 0,202419071 | 0,170184849 |
4) Рассчитаем стандартизованные коэффициенты регрессии и коэффициенты раздельной детерминации, оформим в таблице 9.
Таблица 9. Стандартизованные коэффициенты регрессии и коэффициенты раздельной детерминации
| Переменная | Коэффициент чистой регрессии, b | Среднее значение | Среднеквадратическое отклонение, σ | Коэффициент парной корреляции с зависимой переменной, ryx | Коэффициент эластичности, Э | Бэта-коэффициент, β | Коэффициент раздельной детерминации, d2 |
| ВРП в расчете на душу населения (у) | х | 9,83 | 1,83 | 1,00 | х | х | х |
| инвестиции в основной капитал в расчете на душу населения (х1) | 0,003 | 1509,06 | 488,68 | 0,72 | 0,41 | 0,71 | 0,51 |
| уровень экономической активности населения (х2) | 0,051 | 60,26 | 2,92 | 0,20 | х | 0,08 | 0,02 |
| Итого | х | х | х | х | х | 0,927 |
Вывод: Коэффициент эластичности (Э1) показывает, что при увеличении инвестиций в расчете на душу населения на 1% ВРП возрастет на 0,41%, при условии, что экономическая активность будет зафиксирована на среднем уровне. Расчет коэффициента по второму фактору не имеет смысла, поскольку уровень экономической активности – это показатель структуры, уже выраженный в процентах от общей численности трудовых ресурсов.
β-коэффициенты показывают, что если каждый из факторов изменится на свое среднеквадратическое отклонение, то ВРП под воздействием первого фактора изменится на 0,71 своего среднеквадратического отклонения, второго фактора – на 0,04. То есть, большее влияние на изменение ВРП оказывает уровень инвестиций.
Коэффициенты раздельной детерминации показывают вклад каждого фактора в формирование коэффициента множественной детерминации, вклад первого фактора – 0,51, второго – 0,02. Сумма частных коэффициентов равна коэффициенту детерминации 0,53.
Итак, при анализе стандартизованных коэффициентов регрессии и коэффициентов раздельной детерминации было выявлено, что на уровень валового регионального продукта в расчете на душу населения влияние различий в уровне инвестиций сильнее, чем различий в уровне экономической активности населения.
