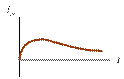Переходные процессы в линейных электрических цепях

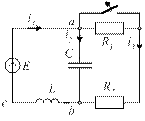
4.1. Какие токи и напряжения приведенной цепи останутся неизменными в момент коммутации?

4.1) ток i₁ и напряжение u_ab

4.2. Постройте график зависимости от времени переходного тока .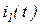

4.2)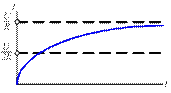

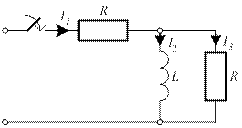
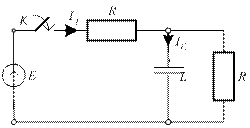4.3. Для приведенной цепи постройте график зависимости от времени переходного тока .

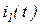4.3)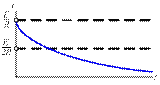

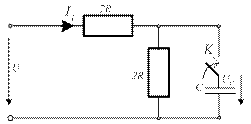
4.4. Для приведенной цепи постройте график зависимости от времени напряжения u_C(t).

4.4)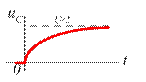

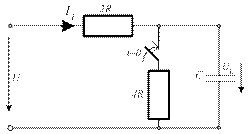4.5. Для приведенной цепи постройте график зависимости от времени напряжения u_C(t).

4.5)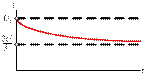

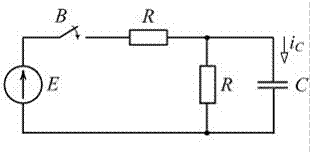
4.6. Для представленной схемы определите установившийся ток конденсатора i_с(0_-) до коммутации.

4.6) i_с(0_-)= 0

Так как в цепи действует источник постоянной ЭДС Е, то установившаяся (принужденная) составляющая тока в ветви с емкостным элементом равна нулю.

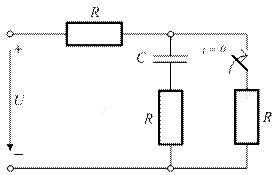4.7. Для представленной схемы запишите начальное условие дифференциального уравнения задачи классического метода анализа переходных процессов.

4.7)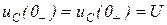

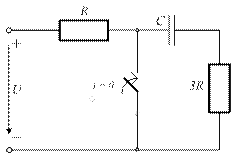4.8. Для представленной схемы запишите начальное условие дифференциального уравнения задачи классического метода анализа переходных процессов.

4.8)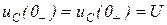

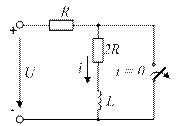4.9. Для представленной схемы запишите начальное условие дифференциального уравнения задачи классического метода анализа переходных процессов.

4.9)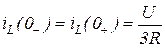

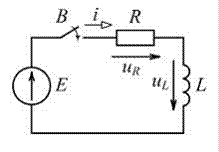4.10.Для представленной схемы определите напряжение на индуктивности U_L(0_-) в первый момент после коммутации.

4.10) U_L(0₊) = Е

До замыкания выключателя В ток в индуктивном элементе был равен нулю, следовательно в первый момент после замыкания выключателя ток также равен нулю: 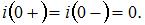По второму закону Кирхгофа 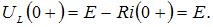Напряжение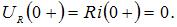

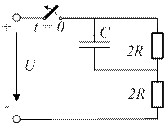
4.11. Определите постоянную времени переходного процесса τ.

4.11) τ = 2RC

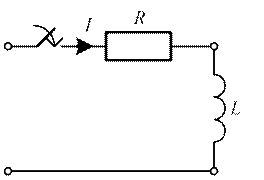
4.12. Определите постоянную времени переходного процесса τ, если R = 1 Ом, а L = 2 мГн.

4.12)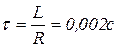

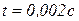4.13. Во сколько раз уменьшится свободная составляющая i_св по сравнению с начальным значением за время , если R = 1 Ом, а L = 2 мГн?

4.13) в е раз

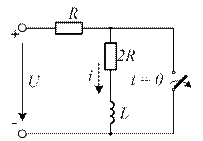
4.14. Определите постоянную времени переходного процесса τ по параметрам схемы цепи.

4.14)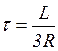

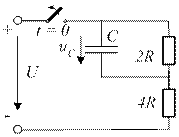4.15. Для представленной схемы составьте уравнение, определяющее закон изменения напряжения u_C(t).

4.15)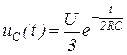

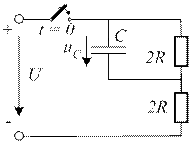* 4.16. Для представленной схемы составьте уравнение, определяющее закон изменения напряжения u_C(t).

416)

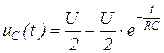
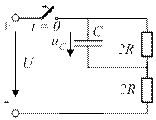4.17. Для представленной схемы составьте уравнение, определяющее закон изменения напряжения u_C(t).

4.17)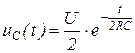

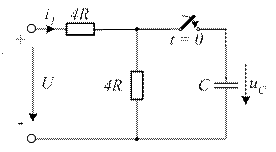4.18. Для представленной схемы составьте уравнение, определяющее закон изменения напряжения u_C(t).

4.18)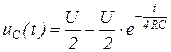

*4.19. Для представленной схемы составьте уравнение, определяющее закон изменения напряжения u_C(t).

4.19)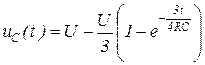

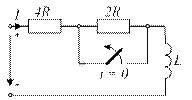
*4.20. Для представленной схемы составьте уравнение, определяющее закон изменения тока i_L(t).

4.20)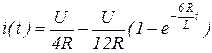

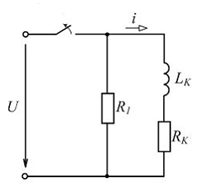
4.21. Определите выражение для тока катушки i(t) после ее отключения от источника постоянного напряжения.

4.21)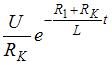

В переходном режиме 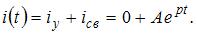Характеристическое уравнение 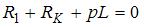имеет корень 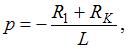а постоянная интегрирования А с учетом начальных условий равна 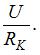Таким образом,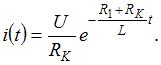

4.22. Составьте характеристическое уравнение схемы.

4.22)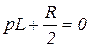

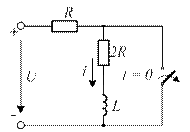4.23. Составьте характеристическое уравнение схемы.

4.23)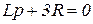

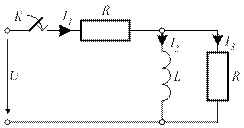
4.24. Составьте характеристическое уравнение схемы

4.24)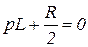

4.25. Составьте характеристическое уравнение схемы

4.25)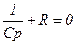

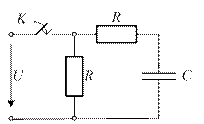
4.26. Составьте характеристическое уравнение схемы

4.26)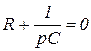

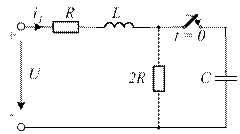* 4.27. Характеристическое уравнение приведенной схемы имеет два одинаковых действительных отрицательных корня. Приведите общее выражение, определяющее закон изменения свободного тока i_св(t).

4.27)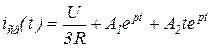

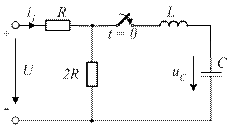* 4.28. Характеристическое уравнение приведенной схемы имеет два одинаковых действительных отрицательных корня. Приведите общее выражение, определяющее закон изменения свободного напряжения u_Cсв(t).

4.28)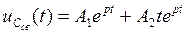

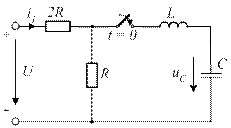4.29. Характеристическое уравнение приведенной схемы имеет два одинаковых действительных отрицательных корня. Приведите общее выражение, определяющее закон изменения свободного напряжения u_Cсв(t).

4.29)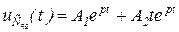

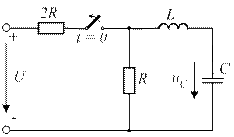4.30. Характеристическое уравнение приведенной схемы имеет два комплексных сопряженных корня р_1,2 = -а ± jω. Приведите общее выражение, определяющее закон изменения свободного напряжения u_Cсв (t).

4.30)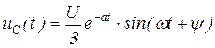

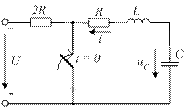4.31. Характеристическое уравнение приведенной схемы имеет два одинаковых действительных отрицательных корня. Приведите общее выражение, определяющее закон изменения свободного напряжения u_Cсв (t).

4.31) ?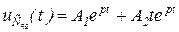

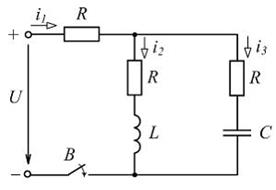4.32.Характеристическое уравнение приведенной схемы имеет два одинаковых действительных отрицательных корня. Приведите общее выражение, определяющее закон изменения переходного тока i₃(t).

4.32)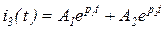

Так как к цепи приложено постоянное напряжение U, то установившееся значение тока в ветви с емкостным элементом 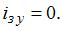Для приведенной цепи с двумя энергоемкими элементами (L и C) характеристическое уравнение имеет вторую степень. Если корни этого уравнения 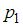и 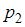действительные и различные, то свободная составляющая тока 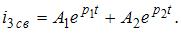Ток

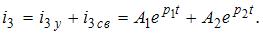
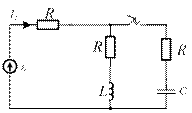
4.33. Постройте операторную схему замещения, соответствующую приведенной схеме цепи после коммутации.

4.33)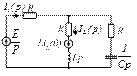

4.34. Постройте операторную схему замещения, соответствующую приведенной схеме цепи после коммутации.

4.34)

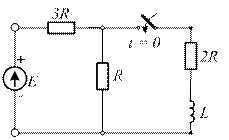4.35. Постройте операторную схему замещения, соответствующую приведенной схеме цепи после коммутации.

4.35)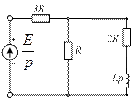

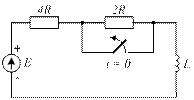4.36. Постройте операторную схему замещения, соответствующую приведенной схеме цепи после коммутации.

4.36)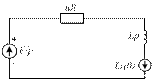

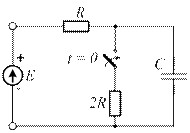
4.37. Постройте операторную схему замещения, соответствующую приведенной схеме цепи после коммутации.

4.37)

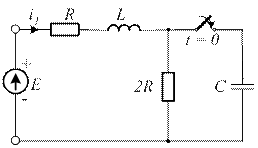
4.38. Постройте операторную схему замещения, соответствующую приведенной схеме цепи после коммутации.

4.38)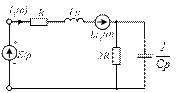

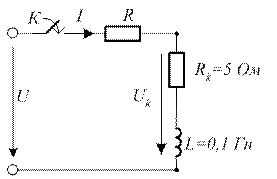4.39. Определите переходное напряжение u_кпер если переходной ток 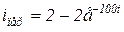А.

4.39)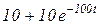

Напряжение на катушке 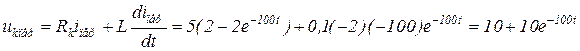В.

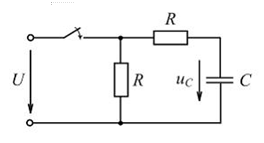
4.40. Определите постоянную интегрирования А, еслипереходное напряжение на конденсаторе u_Cпер = u_Cу + Аe^pt .

4.40) А = -U

4.41. Определите условия, при которых переходной процесс цепи будет носить колебательный характер, если характеристическое уравнение цепи имеет вид .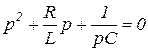

4.41)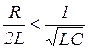

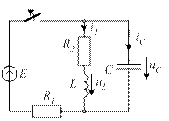4.42. Определите корни р₁ и р₂ характеристического уравнения приведенной схемы цепи, если известны R₁ = R₂ =40 Ом, L = 1 Гн, С = 3330 мкФ. с^-1.

4.42) р₁ ≈ -9,65 с^-1, р₂ ≈ -30 с^-1

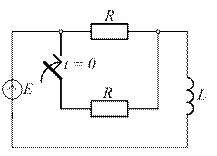
4.43. Для приведенной схемы цепи определите скорость нарастания тока 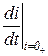в первый момент после коммутации, если U = 50 B, R = 10 Ом, а L = 0,2 Гн.

4.43) 250 А/с

4.44. Постройте качественный график зависимости свободной составляющей тока 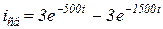при переходном процессе.

4.44)