Дифференциальные трансформации

Более точное представление о геоэлектрическом разрезе, по сравнению с асимптотической интерпретацией, описанной в предыдущем разделе, даёт следующий шаг экспресс-анализа, опирающийся на дифференциальные и алгебраические трансформации кривых кажущегося сопротивления МТЗ. Дифференциальные трансформации основаны на асимптотических представлениях о поведении импеданса магнитотеллурического поля для двух предельных моделей. Модель I типа 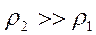соответствует случаю, когда проводник залегает на поверхности изолятора, например, ей соответствует модель осадочного чехла, залегающего на поверхности плохо проводящего кристаллического фундамента. Модель II типа 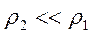соответствует случаю, когда изолятор залегает на поверхности проводника, например, ему соответствует модель плохо проводящего кристаллического фундамента (литосферы), подстилаемого проводящей астеносферой.

Модель I в определенном частотном диапазоне ( 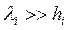) соответствует восходящая асимптота под углом 63⁰25’ к оси абсцисс, и модели II соответствует нисходящая асимптота под углом -63⁰25’ к оси абсцисс. Для приведенных моделей выше были получены выражения (10.3) и (10.7, 10.13), которые могут рассматриваться как выражения для суммарной (действующей) продольной проводимости 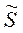проводящего слоя на поверхности изолятора (10.3) и средней (действующей) глубины 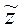до кровли проводящего основания, залегающего под изолятором (10.7, 10.13). Выпишем еще раз эти выражения, приведенные к физической размерности СИ

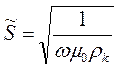(10.14) 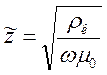(10.15);

Выражения (10.14) и (10.15) могут быть использованы для оценки параметров разреза путем вычисления действующей продольной проводимости 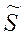и действующей глубины 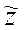в любой точке кривой кажущегося сопротивления МТЗ или графически путем построения S и h асимптотик (Рис. 10.1).

Процедура дифференциальной трансформации основана на представлении о том, что проводимость S приповерхностного слоя мощностью H связана с удельным сопротивлением 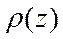в интервале глубин от земной поверхности до глубины H соотношением:

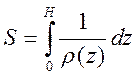(10.16)

Отсюда, продифференцировав 10.16, можно записать:

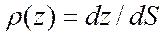(10.17)

Подставляя вместо проводимости S и глубины z действующую проводимость 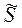и действующую глубину 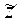, получим аналогичное выражение для действующего сопротивления 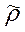, аппроксимирующего истинное :

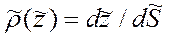(10.18)

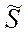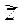Для определения связи и с кажущимся сопротивлением 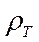применим формулы (10.14) и (10.15), полученные для восходящей и нисходящей ветвей кривых кажущегося сопротивления.

Переходя от частоты 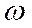к периоду Т, получим:

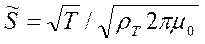(10.19)

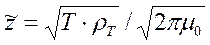(10.20)

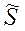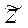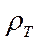При этом, очевидно, и , а следовательно и , являются функциями и 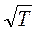. Теперь формулу (10.18) можно записать в виде :

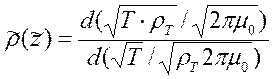(10.21)

Сокращая присутствующий в числителе и знаменателе постоянный множитель 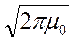, получим :

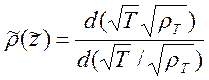(10.22)

После проведения операции дифференцирования, подробно описанной в [Жданов, 1986] искомое в (10.21) выражение для кажущегося сопротивления 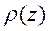на глубине z принимает вид, называемый операцией дифференциальной трансформации Ниблетта-Бостика.

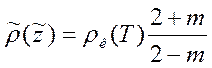, (10.23)

где 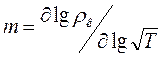(10.24)

Геометрически величина m представляет тангенс угла наклона кривой 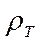относительно оси абсцисс на билогарифмическом бланке 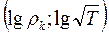. Например, на восходящей ветви двухслойной кривой 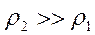(рис 8.1) значение m=2. Это указывает на выход кривой 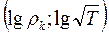на асимптотику с углом наклона 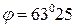^/. Если кривая 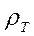имеет угол наклона круче 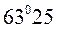^/, то значения 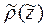в (10.23) принимают отрицательный знак, свидетельствуя о том, что исследуемая кривая 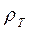не соответствует одномерной горизонтально-слоистой модели. Аналогичные выводы могут быть сделаны при анализе нисходящих ветвей кривых МТЗ.

Недостатком трансформации Ниблетта-Бостика является то, что при выходе кривых кажущегося сопротивления на асимптоту (на угол 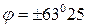) кривая 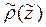терпит разрыв в связи с тем, что значения удельного сопротивления на получаемом разрезе быстро выходят на бесконечность или падают до нуля. Во избежание этих проблем при анализе круто восходящих или нисходящих кривых кажущегося сопротивления используется трансформация Молочнова-Виета, в которой отдельно дифференцируются восходящие и нисходящие ветви. Полученные результаты затем сшиваются в единый разрез .

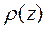На восходящих ветвях кривых 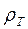(m>0) дифференциальная трансформация Молочнова-Виета имеет вид:

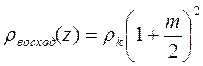(10.25)

На нисходящих ветвях (m<0):

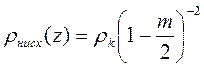(10.26)

Можно видеть, что предельным случаям m=2 и m=-2 в трансформации Молочнова-Виета соответствуют значения 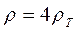и 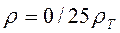, соответственно, то есть, переход от восходящей кривой 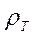к нисходящей не сопровождается переходом через «бесконечность».