Описание установки и вывод расчетной формулы

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ   «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»

Кафедра физики

ЕН.Ф.03 ФИЗИКА

ЕН.Ф.03 ФИЗИКА И БИОФИЗИКА

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Уфа 2006

УДК 531

ББК 22.21

Л 12

Рекомендовано к изданию методической комиссией факультета электрификации и автоматизации с/х (протокол №3 от 30 ноября 2006 года)

Составитель: доцент Амирханов Н.М.

Рецензент: доцент кафедры ТОЭ Желтоухов А.И.

Ответственный за выпуск: зав. кафедрой физики Юмагужин Р.Ю.

Практикум предназначен для всех направлений и специальностей подготовки дипломированных специалистов.

ОГЛАВЛЕНИЕ

	Введение
	Лабораторная работа №1 Изучение законов сохранения импульса и энергии. Определение скорости пули методом баллистического маятника
	Лабораторная работа №2 Изучение вращательного движения и определение моментов инерции тел
	Лабораторная работа №3 Определение коэффициента трения
	Лабораторная работа №4 Изучение гармонических колебаний математического маятника и определение ускорения свободного падения тел
	Лабораторная работа №5 Изучение свободных колебаний пружинного маятника
	Лабораторная работа №6 Определение ускорения свободного падения с помощью оборотного маятника и моментов инерции маятника
	Библиографический список
	Приложение А. Таблица коэффициентов Стьюдента tp,n

Введение

Практикум содержит описания 6 лабораторных работ по механике – науке о механическом движении материальных тел и происходящих при этом взаимодействиях между ними.

Перед занятием студент обязан:

– ознакомиться предварительно с общими сведениями (раздел 1 лабораторной работы) и составить конспект по теоретическому материалу, указанному в начале раздела 3. При этом следует ориентироваться на контрольные вопросы (раздел 4);

– включить в конспект описание и схему установки, краткий вывод расчетной формулы (раздел 2);

– из раздела 3 «Порядок выполнения …» следует перечертить таблицы для результатов измерений, выписать необходимые формулы для расчета как физических величин, так и их погрешностей (при этом не следует переписывать пошаговые инструкции);

– подготовиться к допуску к лабораторной работе по конспекту.

Практикум соответствует требованиям Государственного образовательного стандарта высшего профессионального образования и предназначен для студентов всех направлений, изучающих курс физики.

При выполнении лабораторной работы ряд рисунков и обозначений, приведенных в практикуме, может не совпадать с используемым оборудованием в связи с его модернизацией.

Сборник составлен на основе методических указаний, разработанных преподавателями кафедры физики БГАУ Белобородовой Н.Н., Дусыевым В.М., Лотником С.В., Посняком В.К., Фахретдиновой Э.Ш., Юмагужиным Р.Ю.

Лабораторная работа № 1

Изучение законов сохранения импульса и энергии. Определение скорости пули методом баллистического маятника

Цель и задачи работы: Изучение законов сохранения импульса, энергии. Экспериментальное определение скорости полета пули.

Общие сведения

Пусть тело с массой m движется со скоростью ®u. Тогда это движение можно охарактеризовать двумя физическими величинами: импульсом ®p = m×®u и кинетической энергией W_кин = 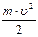. Кроме того тело, поднятое на высоту h над землей (нулевым уровнем), приобретает потенциальную энергию, равную W_пот = m×g×h . Сумма кинетической и потенциальной энергий есть полная механическая энергия тела W = W_кин + W_пот .

Система n тел называется замкнутой, если на нее не действуют внешние силы, при этом тела, входящие в систему, могут взаимодействовать между собой, т.е. на тела могут действовать внутренние силы.

Для замкнутой системы выполняется закон сохранения импульса: сумма импульсов тел замкнутой системы во времени не изменяется

®P = m®u₁ + m®u₂ + … + m®u_n = const.

Для системы n тел (не обязательно замкнутой) выполняется закон сохранения механической энергии, если на нее действуют только консервативные (внешние и внутренние) силы (например, силы тяжести, упругости):

W = W₁ + W₂ + … + W_n = const.

Такие системы называются консервативными.

При наличии внешних неконсервативных сил (например, силы трения) полная механическая энергия системы будет изменяться на величину работы этих сил: DW_незамк = A_неконс.

Описание установки и вывод расчетной формулы

В комплект лабораторной установки входят баллистический маятник, пневматическое ружье, пуля, весы, мерная линейка.

Баллистический маятник (рисунок 1) представляет собой тело 2 с массой M, свободно подвешенное на нерастяжимой нити.

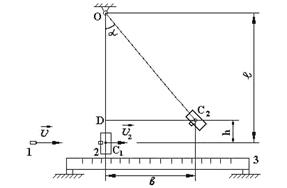
Рисунок 1 Схема лабораторной установки

Вылетевшая из воздушного ружья пуля 1, имея скорость ®u, ударяет в центр маятника 2 (центральный удар). Предполагается, что пуля 1 и тело 2 составляют замкнутую систему. Если в результате удара пуля застревает в теле 2 (абсолютно неупругий удар), система начинает двигаться как единое целое с массой M + m со скоростью ®u₂. Для абсолютно неупругого удара справедлив закон сохранения импульса:

m×®u + M×®u₁ = (M + m)×®u₂, (1)

или в скалярной форме

m×u + M×u₁ = (M + m)×u₂,

где m×u + M×u₁ – импульс системы до удара;

(M + m)×u₂ – импульс системы после удара;

Маятника до удара покоился: u₁ =0, тогда m×u=(M + m)×u₂,а так как M>>m, то m×u = M×u₂ ,

отсюда

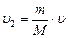_. (2)

Таким образом, в результате удара система «M + m» приобретает кинетическую энергию, с учетом (2):

W_кин = 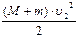= 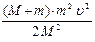_. (3)

Обладая кинетической энергией (3), маятник (система «M + m») максимально отклоняется от вертикали на угол a, при котором центр масс системы из положения С₁ поднимается на высоту h до остановки (положение С₂), так что вся кинетическая энергия (3) системы переходит в потенциальную энергию, равную

W_пот = (M + m) × g h_.

Из закона сохранения энергии для замкнутой системы следует W_кин = W_пот или _.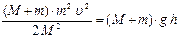

Упрощая уравнение, получаем _.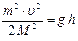

Отсюда скорость пули:

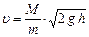_. (4)

Величины m и M определяются взвешиванием, неопределенным в (4) остается параметр h. Из рисунка 1 следует

h = DC₁ = OC₁ – OD = OC₁ – OC₂×cos a = l ×(1 – cos a),

где OC₁ = OC₂ = l – длина нити. Заменяя 1 – cosa = 2sin^{2 a}/₂, получаем h = l × 2sin^{2 a}/₂ .

На данной установке отклонение маятника мало (угол a меньше 4°¸5°), следовательно sin ^a/₂ » ^a/₂ и

h = 2l × ( ^a/₂ )². (5)

При выполнении опыта измерение угла a невозможно, поэтому выразим его через отклонение b. Как следует из рисунка 1 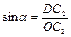или 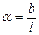. Тогда из (5) следует .

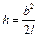Подставляя последнее выражение в (4), окончательно получаем зависимость для скорости пули

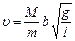_. (6)