Упражнение №1 Действия с матрицами
Используя функции:
МУМНОЖ - Умножение матриц
МОБР - Нахождение обратной матрицы
ТРАНСП - Транспонирование матрицы
МОПРЕД - Вычисление определителя
ИНДЕКС - Извлечение из матрицы элемента по номеру строки и столбца
ЧСТРОК - Определение числа строк
ЧИСЛСТОЛБ - Определение числа столбцов
произведите
1.
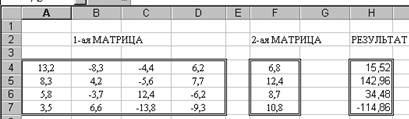 |
Умножение матриц (показано на рисунке):
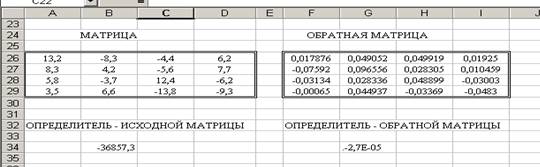
2. Вычисление определителя матрицы и обратной матрицы (показано на рисунке):
 |
3.
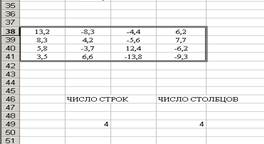 |
Определение числа строк и столбцов (показано на рисунке):
4. Присвоение матрице имени и извлечение элемента из массива с помощью функции Индекс (выполнить самостоятельно. При необходимости использовать Справку).
Упражнение №2 Подбор решения уравнения ( на примере уравнения: х+х2 -4sin(x+0,5) )
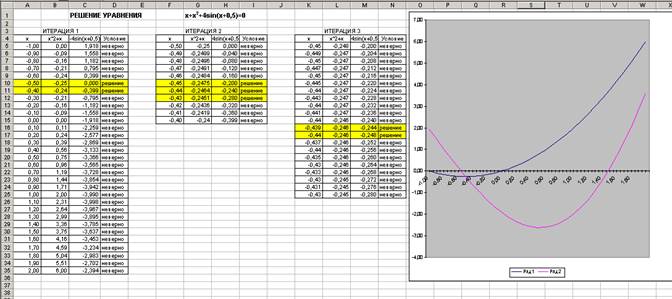
Метод итерации:
- При решении уравнения методом итерации оно разбивается на две части: х+х2 и -4sin(x+0,5)
- Для каждой части строится таблица значений. В четвертой колонке записывается условие: ЕСЛИ (ABS(B14-C14)>0,3;”неверно”;”решение”)
- 0,3 – точность вычисления равенства двух частей уравнения по абсолютной величине (для1-ой итерации). Для последующих итераций точность вычисления возрастает приблизительно на порядок.
- Каждая следующая итерация уточняет диапазон решений, выделенный в предыдущей итерации.
Метод подбора параметров:
- Для этого в произвольно выбранной ячейке (например К30) записывают полную формулу управления: х+х2 - 4sin(x+0,5) .
- А в ячейку L30 вводят начальное значение х, с которого начнется подбор параметра.
- Затем выполняют команду Сервис/Подбор параметра и в диалоговом окне вписывают соответствующие значения.
- После нажатия кнопки ОК появится окно Результата подбора параметров.
Так как при подборе параметра Excel использует итерационный процесс, результат поиска решения путем подбора параметра совпадает с точностью до 3-х знаков с решением методом итераций.
Упражнение №3 Элементарные приемы обработки результатов наблюдений
Теоретическая часть
Обработку результатов наиболее удобно производить с помощью точечных диаграмм. В точечной диаграмме обе оси являются осями значений, поэтому чаще всего они используются для определения типа зависимости между двумя рядами данных.
Например, в электрической цепи замеряются токи и напряжения, причем характеристики проводимости этой цепи заранее неизвестны. Мы знаем, что зависимость тока от напряжения на проводимости чаще всего подчиняется закону Ома.
I=U*G
(т.е. является строго линейной). Однако из курса физики известно, что в технике используются и нелинейные проводимости (термо-, магниторезисторы и др.).
Линии тренда графически иллюстрируют тенденцию изменения рядов данных. Они обычно используются в тех случаях, когда нужно построить диаграммы для задач прогнозирования и экстраполяции.
Регрессия – это статистический метод, позволяющий найти уравнение, которое наилучшим образом описывает множество данных
Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных.
Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Регрессия пропорционально распределяет меру качества по этим трем факторам на основе его спортивных результатов. Результаты регрессии впоследствии могут быть использованы для предсказания качеств нового, непроверенного атлета.
Регрессия использует функцию ЛИНЕЙН.
ЛИНЕЙНАЯ РЕГРЕССИЯ – определяет прямую, которая наилучшим образом представляет можество данных. Функция линейной регрессии возвращает наклон и e-пересечение прямой (точку, в которой прямая пересекает ось Y)
Уравнение линейной регрессии (общий случай):
y=m1x1+m2x2+…+mnxn+b (1)
где у – зависимая переменная, m1…mn коэффициенты при независимых переменных, x1…xn независимые переменные, b – свободный член.
Функции линейной регрессии:
-ЛИНЕЙН -использует выражние (1) и возвращает коэффициентыm1…mn и b
-ТЕНДЕНЦИЯ
-ПРЕДСКАЗ
-НАКЛОН
-CTOYX
Функция ЛИНЕЙН(известные_значения_у;известные_значения_х;конст;статистика)
Известные_значения_у – это множество значений у, которые уже известны для cоотношения y=mx+b.
Известные_значения_х–это необязательное множество хначений х, которые уже известны для соотношения y=mx+b.
Конст - это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
Если конст иеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y=mx.
Статистика – это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.
Если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику (см. справку в Excel) Наиболее важным показателем здесь является коэффициент r2. Это коэффициент детерминированности. Сравниваются фактические значения у и значения получаемые из уравнений прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеент место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями у. В противоположном случае, если коэффициент детермированности равен 0, то уравнение регрессии неудачно для предсказания значений у.
