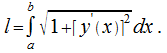Функц-ные ряды.Основные опр-ния
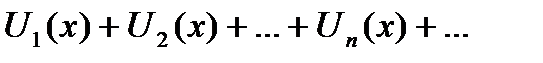 (1) (1) |
| Каждым членом которого является функция от x. |
| Добавим аргументу x различные значения из (1) будем получать различные числовые ряды некоторые из которых сходятся, а некот. расходятся. |
| Множество значений х, при которых функциональный ряд сходится называется областью сходимости функционального ряда. Очевидно, что область сходимости, тоже является функцией от х. |
Площадь криволинейного сектора в полярных коор-тах
Любая точка в полярной системе координат задается полярным углом 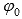 и соответствующим полярным радиусом .
и соответствующим полярным радиусом . 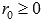
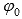 - это угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки), а
- это угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки), а 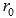 - это расстояние от заданной точки до начала координат (полюса).
- это расстояние от заданной точки до начала координат (полюса).
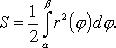
Знакочередующиеся ряды.Признак Лейбница
Теорема Лейбница:
Если в знакочередующемся ряду 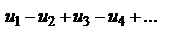 , где
, где 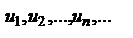 положительны, члены таковы, что
положительны, члены таковы, что 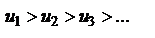 и
и 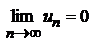 , то ряд сходится, его сумма положительна и не превосходит первого члена.
, то ряд сходится, его сумма положительна и не превосходит первого члена.
Доказательство: Рассмотрим сумму 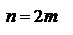 первых членов ряда.
первых членов ряда. 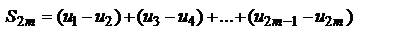 По условию 1 выражение в каждой скобке положительно. Следовательно, сумма
По условию 1 выражение в каждой скобке положительно. Следовательно, сумма 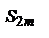 положительна и возрастает с возрастанием m. Запишем теперь эту же сумму так:
положительна и возрастает с возрастанием m. Запишем теперь эту же сумму так:
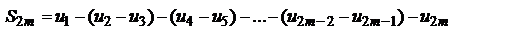 По условию 1 каждая из скобок положительна. Поэтому в результате вычитания этих скобок из
По условию 1 каждая из скобок положительна. Поэтому в результате вычитания этих скобок из 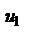 мы получим число, меньшее
мы получим число, меньшее 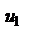 . Таким образом, мы установили, что
. Таким образом, мы установили, что 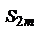 при возрастании m возрастает и ограничена сверху. Отсюда следует, что
при возрастании m возрастает и ограничена сверху. Отсюда следует, что 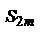 имеет предел S
имеет предел S
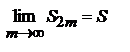 , причем
, причем 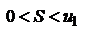 . Однако сходимость еще не доказана. Мы доказали только, что последовательность четных частичных сумм имеет пределом число S. Докажем теперь, что нечетные частичные суммы также стремятся к пределу S. Рассмотрим для этого сумму
. Однако сходимость еще не доказана. Мы доказали только, что последовательность четных частичных сумм имеет пределом число S. Докажем теперь, что нечетные частичные суммы также стремятся к пределу S. Рассмотрим для этого сумму 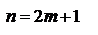 первых членов исходного ряда.
первых членов исходного ряда. 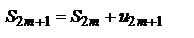 . Так как по условию 2 теоремы
. Так как по условию 2 теоремы 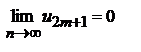 , то следовательно
, то следовательно 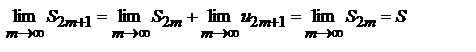 Тем самым мы доказали, что
Тем самым мы доказали, что 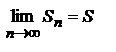 как при четном n, так и при нечетном. Следовательно, исходный ряд сходится.
как при четном n, так и при нечетном. Следовательно, исходный ряд сходится.
! Теорема Лейбница справедлива, если условия выполняются с некоторого N.
44.1.Вычисление длины дуги кривой
Под длиной дуги 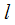 кривой
кривой 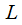 понимается предел, к которому стремится длина вписанной в нее ломанной, если длина самого большого ее звена стемится к нулю.Допустим, что кривая
понимается предел, к которому стремится длина вписанной в нее ломанной, если длина самого большого ее звена стемится к нулю.Допустим, что кривая 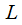 определена уравнением
определена уравнением 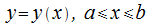 , при этом
, при этом 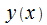 представлена в качестве непрерывно дифференцируемой функции на
представлена в качестве непрерывно дифференцируемой функции на 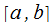 . Разделим ее на
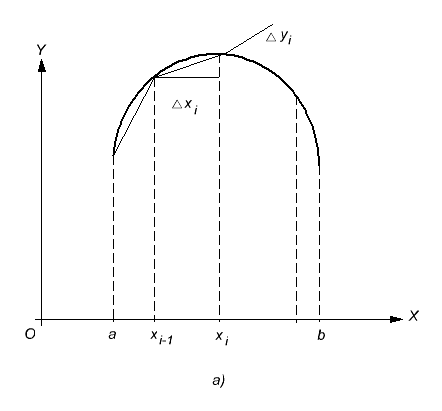
. Разделим ее на 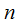 частей посредством точек с абсциссами
частей посредством точек с абсциссами 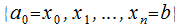 и проведем через данные точки хорды (рис. 18.9, а). В результате имеем вписанную ломанную с длиной
и проведем через данные точки хорды (рис. 18.9, а). В результате имеем вписанную ломанную с длиной 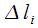 ее
ее 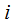 -го звена
-го звена 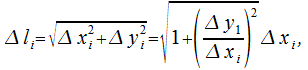
здесь 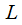 , составляет
, составляет 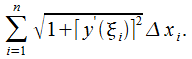 Из определения длины дуги следует
Из определения длины дуги следует 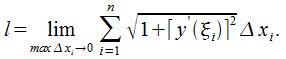 Поскольку правая часть представляет собой интегральную сумму для функции
Поскольку правая часть представляет собой интегральную сумму для функции 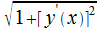 , то (18.1)
, то (18.1)