Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу 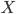 из уравнения
из уравнения 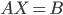 , необходимо умножить это уравнение на
, необходимо умножить это уравнение на 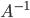 слева.
слева.
Тогда: 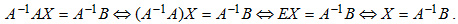
Следовательно, чтобы найти решение 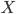 уравнения
уравнения 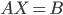 , нужно найти обратную матриц
, нужно найти обратную матриц 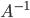 и умножить ее на матрицу
и умножить ее на матрицу 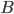 , стоящие в правой части уравнения.
, стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
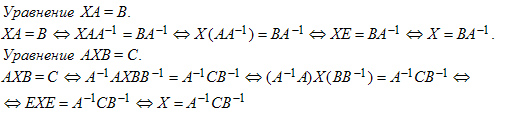
8) Решение линейных систем n-го порядка в матричном виде(в терминах обратной матрицы)
Справедливо следующее утверждение (формулы Крамера).
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1 , x2 , ..., xn, определяемое формулами Крамера
xi =Di / D, i=1,2, ..., n,
где Di - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.
ПРИМЕР 2. Вычисление решения системы линейных уравнений по формулам Крамера.
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn
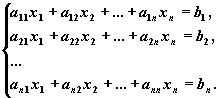
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
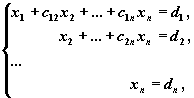
решение которой находят по рекуррентным формулам:
xn =dn , xi = di -S nk=i+1 cik xk , i=n-1, n-2, ...,1.
Матричная запись метода Гаусса.
1. Прямой ход метода Гаусса: приведение расширенной матрицы системы

к ступенчатому виду
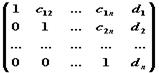
с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:
o перестановка строк;
o умножение строки на число, отличное от нуля;
o сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).
2. Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
 ,
,
последний, (n+1)-й, столбец этой матрицы содержит решение системы.
9) Линейная зависимость(независимость) столбцов матрицы. Ранг матрицы.
Ранг матрицы.
Рассмотрим матрицу А, размером m×n:




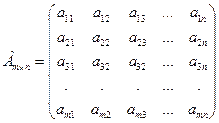
Выделим в ней К строк и К столбцов, где К ≤ min(n;m). Из элементов стоящих на пересечении выделенных строк и столбцов составим определитель К –ого порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделим этот минор. В данный момент – это минор 2 –го порядка. Заметим, что таких миноров можно составить 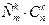 . С – комбинация, где:
. С – комбинация, где:
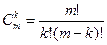 ;
; 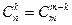
Пример:
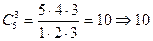 миноров
миноров
Наивысший порядок миноров матрицы, отличительных от 0 называется рангом матрицы.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Ранг матрицы обозначают r(A), rang(A)
Основные свойства ранга матрицы:
1) при транспонировании матрицы, её ранг не меняется
2) если вычеркнуть из матрицы нулевой ряд, то её ранг не изменится
3) ранг матрицы не изменится при элементарных преобразованиях матрицы
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
10) Теорема о базисном миноре
Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ.
Доказательство. Предположим противное - система длинных столбцов линейно зависима 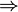 система коротких столбцов (входящих в длинные)
система коротких столбцов (входящих в длинные) 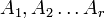 линейно зависима (
линейно зависима ( 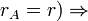 по свойству определителя
по свойству определителя
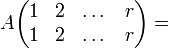 БМ = 0. Противоречие, т.к. БМ
БМ = 0. Противоречие, т.к. БМ 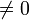 .
.
Без ограничения общности считаем, что базисный минор расположен в левом верхнем углу. Покажем, что i-ый столбец линейно выражается через столбцы из БМ. i > r (иначе он сам является столбцом из БМ). Рассмотрим минор порядка на один больше, он будет нулевой.
Фиксируем 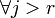 . Раскладываем определитель по j-ой строке:
. Раскладываем определитель по j-ой строке:
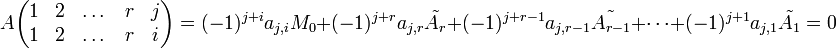 так как минор порядка (r + 1) - нулевой (где M0 - БМ
так как минор порядка (r + 1) - нулевой (где M0 - БМ 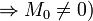 . Выражаем aj,i:
. Выражаем aj,i: 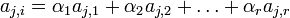 Получены коэффициенты α1,...,αr. Для любого k:
Получены коэффициенты α1,...,αr. Для любого k: 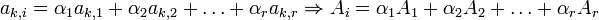 (так как k - любое)
(так как k - любое)
Следствие. Если все столбцы матрицы А линейно выражаются через r столбцов 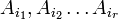 , которые образуют линейно независимую систему, то rA = r.
, которые образуют линейно независимую систему, то rA = r.
Доказательство. Столбцы входящие в максимальную линейно независимую систему (в кол-ве rA штук) линейно выражаются через 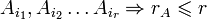 . столбцы
. столбцы 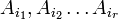 (в кол-ве r штук) линейно выражаются через максимальную линейно независимую систему в кол-ве
(в кол-ве r штук) линейно выражаются через максимальную линейно независимую систему в кол-ве 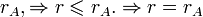 .
.
11) Методы вычисления ранга матрицы и нахождения базисного минора

12) Линейные системы уравнений общего вида. Их элементраные преобразования. Метод гаусса решения таких систем.
Систему m линейных уравнений с n неизвестными будем записывать в следующем виде:

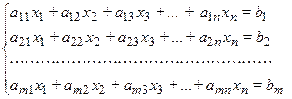 .
.
Сформулируем теперь кратко суть метода Гаусса. Полагая, что в системе коэффициент a11 отличен от нуля ( если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1 и переобозначить коэффициенты), преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью эквивалентных преобразований описанным выше способом.
В полученной системе

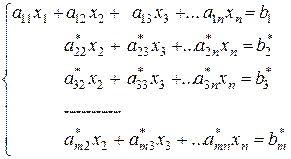 ,
,
считая, что 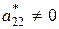 (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений и переобозначив коэффициенты системы), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
(что всегда можно получить, переставив уравнения или слагаемые внутри уравнений и переобозначив коэффициенты системы), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
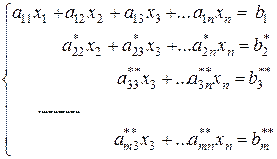
при условии 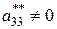 оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:
1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;
2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;
3) если получается система с трапецеидальной матрицей коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.
13) Однородные системы уравнений. Ранг матрицы и существование нетривиального решения.
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
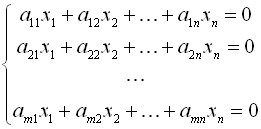
Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что 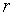 не превосходит
не превосходит 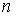 . В случае
. В случае 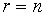 система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при
система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при 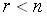 .
.
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство: Если у системы уравнений 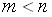 , то ранг
, то ранг 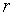 системы не превышает числа уравнений
системы не превышает числа уравнений 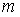 , т.е.
, т.е. 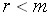 . Таким образом, выполняется условие
. Таким образом, выполняется условие 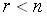 и, значит, система имеет ненулевое решение.
и, значит, система имеет ненулевое решение.
Следствие 2: Однородная система 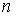 уравнений с
уравнений с 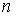 неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
Доказательство: Допустим, система 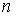 линейных однородных уравнений, матрица которой
линейных однородных уравнений, матрица которой 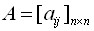 с определителем
с определителем 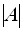 , имеет ненулевое решение. Тогда по доказанной теореме
, имеет ненулевое решение. Тогда по доказанной теореме 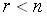 , а это значит, что матрица
, а это значит, что матрица 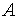 вырожденная, т.е.
вырожденная, т.е. 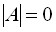 .
.
Разрешенные системы линейных уравнений
Переменная 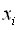 называется разрешенной, если какое-нибудь уравнение системы содержит
называется разрешенной, если какое-нибудь уравнение системы содержит 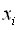 с коэффициентом, равным единице, а во все остальные уравнения системы переменная
с коэффициентом, равным единице, а во все остальные уравнения системы переменная 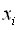 не входит, т.е. входит с коэффициентом, равным нулю.
не входит, т.е. входит с коэффициентом, равным нулю.
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
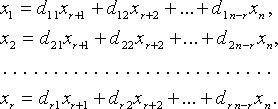
Тогда n - r линейно независимыми вектор-решениями будут:
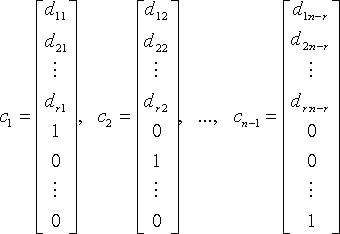
а любое другое решение является их линейной комбинацией. Вектор-решения 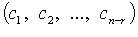 образуют нормированную фундаментальную систему.
образуют нормированную фундаментальную систему.
В линейном пространстве 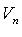 множество решений однородной системы линейных уравнений образует подпространство размерности n - r;
множество решений однородной системы линейных уравнений образует подпространство размерности n - r; 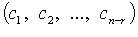 - базис этого подпространства.
- базис этого подпространства.
14) Структура общего решения однородной системы уравнений.
AX=0 (1)
Если Х1 Хn – решение системы, то любая их линейная комбинация , тоже решение этой системы уравнений.
АХ1 = 0 АХ2 = 0 AXn = 0
A( 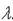 1 X1 +
1 X1 + 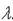 2 X2 + … +
2 X2 + … + 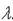 n Xn)=
n Xn)= 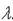 1 A X1+
1 A X1+ 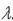 2 A X2 +…+
2 A X2 +…+ 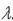 n A Xn = 0
n A Xn = 0
(то что в скобках) – линейная комбинация
Теорема: Пусть r = rank A<n , тогда существует (n-r) линейно независимое решение системы (1). А все остальные решения представляются, как их линейная комбинация.
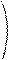
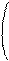 Определение: Набор линейно-независимых решений называется набором фундаме6нтальных решений системы (1).
Определение: Набор линейно-независимых решений называется набором фундаме6нтальных решений системы (1).
АХ=0 Х1
А – матричный коэффициент Х= ...
А – m x n – матрица Хn
r = rank A<n
Тогда:
1. Существует (n – r) решение системы (1)
2. Все остальные решения являются линейными коэффициентами (n – r) решений
Определение: Эти решения называются функцией решений
 Доказательство:
Доказательство:
U1 U2 . . . Un – Столбцы матрицы А
X1U1 + x2U2 +. . . + xnUn = 0
По теореме о базисном миноре столбец Uk, является линейной комбинацией базисных столбцов.
Uk = 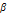 1U1 +
1U1 + 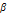 2U2 + . . . +
2U2 + . . . + 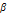 nUn
nUn
Uk – 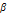 1U1 –
1U1 – 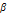 2U2 – . . . –
2U2 – . . . – 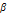 nUn = 0
nUn = 0
Сравним строчку 1, со строкой 1. Числа (- 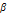 1
1 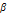 2 …
2 … 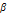 r, 0 . . . 1, 0)
r, 0 . . . 1, 0)
 1 – k
1 – k
Xk = - 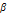 1
1
- 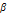 2
2
- 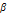 r - столбец решений
r - столбец решений
0 Покажем, что столбцы независимы.
1 Пусть существуют числа: 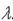 r+1,
r+1, 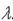 r+2 . . .
r+2 . . . 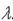 n , такие что
n , такие что
0 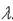 r+1 Xr+1 +
r+1 Xr+1 + 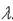 r+2 Xr+2 + . . . +
r+2 Xr+2 + . . . + 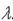 n Xn = 0 (2)
n Xn = 0 (2)
 | |||||||
 | |||||||
 | |||||||
 | |||||||
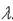 r+1 = 0 =>
r+1 = 0 => 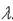 r+1 =
r+1 = 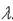 r+2 = . . . =
r+2 = . . . = 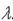 n = 0
n = 0
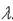 r+2
r+2
Равенство (2) может выполнятся, только если вес 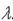 = 0, значит столбцы Хк – линейна независима
= 0, значит столбцы Хк – линейна независима
Доказательство 2: Пусть z – столбец решений системы (1)
Z = Z1
Z2
Z r+1
. . .
Zn
Y = Z – Z r+1 X r+1 – Z r+2 X r+2 - . . . – Zn Xn
Все столбцы Z и Х, решение наших уравнений, значит У тоже является решением уравнений
Y= Y1
Y2
Yn Y1U1 +Y2 U2 + . . . + Yr Ur = 0 (3)
0 r
0 r+1
Y1, Y2 – базисные столбцы нашей матрицы, линейно независимы, соотношение (3) выполняется только в 1 случае, когда все y =0 => столбец х=0 => Z = Zr+1 Xr+1 + Zr+2 Xr+2 + . . . +ZnXn (6)
Строчка (6) означает, что столбец “z” является линейной комбинацией столбцов X
Любое решение системы (1), имеет следующий вид : x = 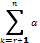 k Xk
k Xk
Фундаментальное решение – эта формула описывает общее решение однозначной системы уравнения.
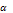 – принимает решения, которые возникали в процедуре Гауса.
– принимает решения, которые возникали в процедуре Гауса.
15) Неоднородные системы уравнений общего вида. Теорема Кронекера-Капелли
А11 х1 + а12 x2 + . . . +a1n x1n = b1
A21 x1 + a22 x2 + . . . +a2n x2n = b2
. . . система 1 AX = B
An1 x1 + an2 x2 + . . . + amn xn = bm
A = {aik} матричный коэффициент
B = (b1 ) - столбцы первых частей
(bm)
Х = (х1) -
(хn)
Теорема Кронекера-Капели.
Для того что бы система уравнений (1) имела решение, необх. и дост.,что б выполнялось:
Rank A = rank  A
A
Где  A – расширенная матрица
A – расширенная матрица
Система линейных алгебраических уравнений (1) совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Выводы из теоремы:
1)если ранг совместной системы равен числу неизвестных, то система имеет единственное решение
2)если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений
3)ранг основной матрицы не может быть больше ранга расширенной матрицы
16) Строение множества решений неоднородной системы уравнений общего вида.
Общее решение неоднородной системы линейных уравнений равно сумме общего решения приведенной однородной системы и любого частного решениянеоднородной системы.
Поскольку общее решение линейной системы, записанной в каноническом виде, определяется формулами:
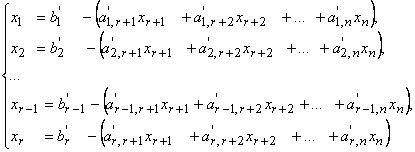
то общее решение неоднородной системы можно записать в векторной форме в виде:
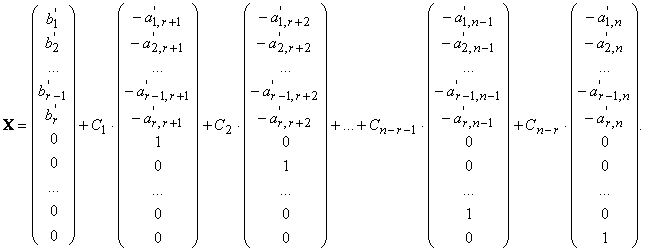
Здесь С1, С2, ..., Сn−r−1, Сn−r — произвольные константы, r — ранг матрицы системы.
17) Векторное пространство. Операции над векторами. Линейная независимость
Линейные операции над векторами.
Под линейными операциями над векторами понимают операции сложения, вычитания векторов, а так же умножение вектора на число.
Пусть а и b произвольные вектора, возьмем произвольную точку 0 и построим вектор ОА= а и ОВ = b




 A
A
а
a+b
 b
b
O B
В таком случае сумма векторов производится по правилу параллелограмма.
Если начало и конец векторов соответствуют, то сумма векторов производится по правилу треугольника.


 b
b
а a+b

a2

 a1
a1
a3


 an-1
an-1
 a1+..+an
a1+..+an
an
Под разностью векторов а и b понимается вектор с, такой что b + c = a
 a a – b = a + (-b)
a a – b = a + (-b)
a
c
b
Отметим, что в параллелограмме, построенном на векторах а и b, одна направленная диагональ является суммой векторов а и b, а другая разностью векторов. Можно вычитать векторы по правилу: а – b = a + (-b), то есть вычитание векторов заменить сложением вектора а с вектором противоположным вектору b.
Произведение а на скаляр.
Произведением вектора а на скаляр, называется вектор λа, который имеет длину │λ│∙│а│, коллинеарен вектору Q, имеет направление вектору а, если λ › 0 и противоположен по направлению, если λ ‹ 0.
Пример:

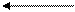
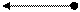
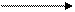 а b
а b
2a -3b
Из определения произведения векторов на число следуют свойства этого произведения:
1) если b = λa , то b параллелен а
если а параллелен b и а ≠ 0, то при некотором λ, верно равенство λb = a
2) всегда а = │а│∙ а-0 ,где а-0 - орта вектора а .
то есть каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1) а + b = b + a
2) (a + b) + c = a + (b + c)
3) λ1(λ2a) = λ1λ2a
4) (λ1+ λ2)a = λ1a + λ2a
5) λ(a + b) = λa + λa
Эти свойства позволяют проводить преобразования в линейных операциях с вектором, как это делается в обычном алгебре: слагаемые меняют местами, вводят скобки, группируют, выносят за скобки, как скалярные, так и векторные общие множители.
18) Базис пространства. Размерность пространства

19) Связь между различными базисами.
Если в базисе 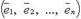 линейный оператор
линейный оператор 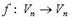 имеет матрицу A, в базисе
имеет матрицу A, в базисе 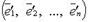 - матрицу B, а S - матрица перехода от первого базиса ко второму, то
- матрицу B, а S - матрица перехода от первого базиса ко второму, то 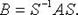
20) Преобразование координат при замене базиса.
1 Пусть матрица С описывает связь между базисами fs = 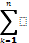 cks ln
cks ln
Возьмём вектор U.
Этот вектор можно представить, как линейную комбинацию векторов { l1, l2…ln}
U = 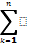
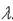 k ln
k ln
координата U в базисе {e } - 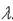
2. Линейная комбинация {f1, f2 … fn}
U = 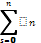 s fs
s fs
Вопрос: как связаны координаты?
{ 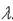 1
1 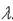 2…
2… 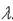 n} и коэфицент {n1…nr}?
n} и коэфицент {n1…nr}?
Утверждение: координаты, в данном базисе определяются однозначно.
Доказательство: Пусть не так, u= 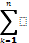
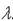 1 lk =
1 lk = 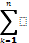 Mk lk
Mk lk
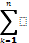 (Mk – lk) lk = 0
(Mk – lk) lk = 0
Mk = 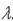 k
k 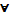 k
k
U= 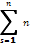 s fs =
s fs = 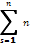 s (
s ( 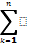 cks lk) =
cks lk) = 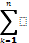 lk (
lk ( 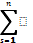 lks ns)=
lks ns)= 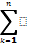
Координаты определяются однозначно => 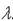 =
= 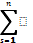 lns ns
lns ns
Эта формула описывает связь между координатами.
21) Линейные операторы и их матричная форма.

22) Действия с линейными операторами.
Для линейных операторов, как и для всех других новых объектов, с которыми мы познакомились в курсе линейной алгебры, можно определить линейные операции — операции сложения и умножения на число.
Определение. Суммой операторов Aи Bназывается оператор, определенный в Rn на 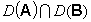 и действующий следующим образом:
и действующий следующим образом: 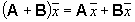 .
.
Определение. Произведением оператора Aна число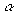 называется оператор, определенный в Rn на
называется оператор, определенный в Rn на 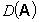 и действующий следующим образом:
и действующий следующим образом: 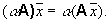
Определение. Произведением AB операторов Aи B называется оператор, определенный в Rn на 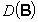 и действующий следующим образом:
и действующий следующим образом: 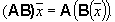
На лекции доказано, что сумма линейных операторов, произведение линейного оператора на действительное число и произведение линейных операторов — линейный оператор.
Нетрудно доказать следующее утверждение: матрица суммы операторов в некоторм базисе равна сумме матриц слагаемых в том же базие, матрица оператора, являющегося произведением оператора на число — произведению матрицы оператора на число, а матрица произведения операторов — произведение матриц сомножителей.
23) Преобразование матрицы линейного оператора при переходе к новому базису.
Так как матрица линейного оператора, очевидно, зависит от выбранного базиса, то возникает вопрос: как изменится матрица оператора при переходе к другому базису? Выясним это.


Замечание. Квадратные матрицы и , для которых найдется невырожденная матрица T такая, что имеет место равенство , называются подобными
24) Собственные числа и собственные вектора линейного оператора
Ненулевой вектор 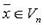 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 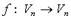 , если
, если 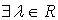 (
( 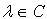 для комплексного
для комплексного 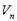 ), такое, что
), такое, что 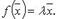 Число
Число 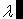 называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.
называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.
Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор 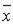 имеет координатный столбец X, то
имеет координатный столбец X, то 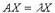 или
или 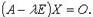
Собственные числа 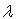 линейного оператора
линейного оператора 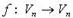 - корни характеристического уравнения
- корни характеристического уравнения 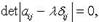 , где
, где 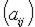 - матрица оператора f,
- матрица оператора f, 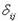 - символ Кронекера.
- символ Кронекера.
Для каждого собственного значения 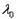 соответствующие собственные векторы могут быть найдены из матричного уравнения
соответствующие собственные векторы могут быть найдены из матричного уравнения 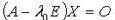 или соответствующей ему системы линейных уравнений
или соответствующей ему системы линейных уравнений
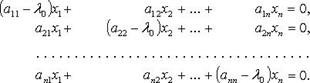
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид

где 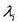 - соответствующие собственные значения.
- соответствующие собственные значения.
25) Переход к базису собственных векторов, когда все собственные числа различны.
26) Квадратичные формы. Приведение к диагональному виду
Метод Лагранжа
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
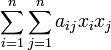
есть данная квадратичная форма. Возможны два случая:
1. хотя бы один из коэффициентов aii при квадратах отличен от нуля. Не нарушая общности, будем считать 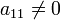 (этого всегда можно добиться соответствующей перенумерацией переменных);
(этого всегда можно добиться соответствующей перенумерацией переменных);
2. все коэффициенты 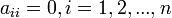 , но есть коэффициент
, но есть коэффициент 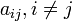 , отличный от нуля (для определённости пусть будет
, отличный от нуля (для определённости пусть будет 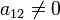 ).
).
В первом случае преобразуем квадратичную форму следующим образом:
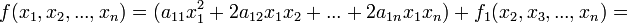
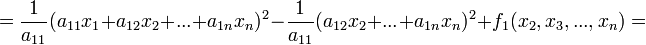
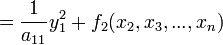 , где
, где 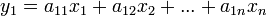 , а через
, а через 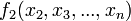 обозначены все остальные слагаемые.
обозначены все остальные слагаемые. 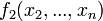 представляет собой квадратичную форму от n-1 переменных
представляет собой квадратичную форму от n-1 переменных 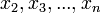 .С ней поступают аналогичным образом и так далее.
.С ней поступают аналогичным образом и так далее.
Заметим, что 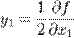 Второй случай заменой переменных
Второй случай заменой переменных 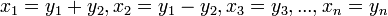 сводится к первому.
сводится к первому.
27) Инерция квадратичных форм
Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.
В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.
В этом базисе квадратичная форма имеет канонический вид
k(x) = λ1x12 + λ2x22 + ... + λnxn2.
Числа λ1, λ2, ... , λn — канонические коэффициенты квадратичной формы.
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.
Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
28) Скалярное произведение векторов. Длина вектора. Проекция вектора на ось. Угол между векторами.
Скалярное произведение векторов и его свойства.
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.
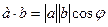 (1)
(1)
где φ – угол между векторами а и b
Формуле (1) можно придать иной вид, так как │а│cosφ = прba и │b│cosφ = праb , то получим:
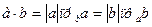 (2)
(2)



а
φ
b
То есть Скалярное произведение двух векторов равно модулю одного из них, умноженного на проекцию другого на ось.
Свойства скалярного произведения:
1) Скалярное произведение обладает переместительным свойством.
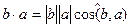
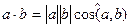
так как │а││b│= │b││a│, cos(a,b) = cos(b,a), то ab = ba
2)Скалярное произведение обладает сочетательным свойством, относительно скалярного множителя.
(λa)b = λ (ba)
(λa)b = │b│прbλa = λ│b│прba = λ (ab)
3) Скалярное произведение обладает распределительным свойством:
a(b + с) = ab + ac
a(b + c) = │a│пра(b+c) = │a│(прab+прac) = │a│прab+│a│прaс = ab + ac
4) Скалярный квадрат вектора равен квадрату его длины.
а2 = │а│2
а2 = а∙а = │а│∙│а│cos1 = │а│∙│а│= │a│2
В частности i2 = j2 = k2 = 1
Если а возвести скалярно в квадрат и затем извлечь корень, то получим не первоначаль-
ный вектор, а его модуль. 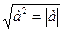
Пример:
Найти длину вектора с=3а-4b, если │а│=2;│b│=3; (a,b)=π\3
Решение:
│с│= 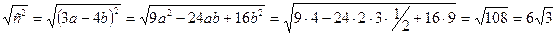
5)Если вектора a и b ненулевые, взаимно перпендикулярны, то их скалярное произведение равно 0.
Следовательно верно и обратное утверждение: если произведение векторов а и b равно 0, значит вектора взаимно перпендикулярны.
В частности: ij = jk = ki = 0
Выражение скалярного произведения через координаты.
Пусть заданы два вектора а = ахi + аyj + аzk и b = bхi + byj + bzk. Найдем скалярное произведение векторов, перемножая их, как многочлены и пользуясь таблицей скалярных произведений векторов i, j, k
| i | j | k | |
| i | |||
| J | |||
| k |
a∙b = (ахi + аyj + аzk)( bхi + byj + bzk)= ахbх + аyby + аzbz
То есть a∙b = ахbх + аyby + аzbz
Пример: доказать что диагонали четырехугольника, заданного координатами вершин А(
-4;-4;4), В(-3;2;2), С(2;5;1) и D(3;-2;2), взаимно перпендикулярны.
Решение:
Составим вектора АС и ВD, лежащие на диагоналях данного четырехугольника, имеем:
АС(2-(-4);5-(-4);1-4)=(6;9;3) и BD(6;-4;0)
Найдем скалярное произведение этих векторов:
АС∙BD = 6∙6+9(-4)+0(-3) = 36-36 = 0
Следовательно вектор АС перпендикулярен вектору BD, значит диагонали четырехугольника ABCD взаимно перпендикулярны.
Проекция вектора на ось.
 |
Пусть в пространстве задана ось l α







M
M1 L
Проекции точки М на ось l называется основание перпендикуляра ММ1 опущенного из точки на ось. Точка М1 – есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси. Если точка М лежит на оси l, то проекция точки М на ось совпадает с М.
Пусть АВ - произвольный вектор. │АВ│≠ 0. Обозначим через А1 и В1 проекции на ось l соответственно начало А и конец В вектора АВ и рассмотрим вектор А1В1
Проекции вектора АВ на ось l называется положительное число │А1В1│, если вектор А1В1 и ось l одинаковы направлены, и отрицательное число - │А1В1│, если вектор А1В1 и ось l противоположно направлены.












 |  |
А В
 А1 В1 l (и соотв
А1 В1 l (и соотв
наоборот)
Если точки А1 и В1 совпадают (│А1В1│=0), то проекцией вектора АВ=0. Проекция вектора АВ на ось l обозначается: прlАВ. Если АВ = 0 или АВ перпендикулярен к оси l, то прlАВ=0.
Угол φ между вектором а и осью l изображен на рисунке:
 |
A
 φ l
φ l

Рассмотрим некоторые основные свойства проекции:
1) Проекция вектора а на ось l равна произведению модуля вектора а на cosφ
прl а= │а│∙ cosφ
Если 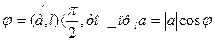
Если 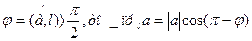
Если 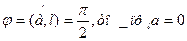
Следствие 1. Проекция вектора на ось положительна (отрицательна), если вектор образует острый (тупой) угол и равна 0, если этот угол прямой.
Следствие 2. Проекции равных векторов на одну и туже ось равны между собой.
2) Проекция суммы нескольких векторов на одну и туже ось равна сумме их проекций на эту ось. d = a + b + c ; прl(a+b+c) = прla + прlb + прlc




 b
b
 |  |
a с
d



 a b l
a b l
d c
3) При умножении вектора а на число λ, его проекция на ось также умножается на это число: прl(λa) = λ прla
при λ›0 имеем: прl(λa) = │λa │cosφ = λ│a│ cosφ = λ прla
при λ‹0 имеем прl(λa) = │λa │cos(π-φ) = -λ│a│(-cosφ) = λаcosφ = λ прla
свойство спра ведливо при λ = 0
Угол между векторами.
Определение угла φ между векторами а (ах; аy; аz) и b(bх; by; bz)
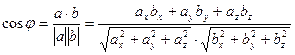
Отсюда следует условие перпендикулярности ненулевых векторо a и b:
ахbх + аyby + аzbz = 0
29) Векторное произведение, смешанное произведение векторов. Их геометрический смысл.
Векторное произведение векторов и его свойства.
Векторным произведением вектора а на b называется вектор с, который
1) перпендикулярен векторам а и b









 2) имеет длину численно равную площади параллелограмма, построенного на векторах а и b.
2) имеет длину численно равную площади параллелограмма, построенного на векторах а и b.
С │c│=│a││b│sinφ
B S
φ
b
3)Вектора a,b,c образуют правую тройку
а × b; [a,b]




Из определения векторного произведения непосредственно вытекают следующие отношения между ортами i, j,k
i × j = k ; j × k = i ; k × i = j
Докажем, например, что i × j = k:
1)k перпендикулярен к i; k перпендикулярен к j
2)│k│=1, но │i × j │=│i│×│j│sin900 = 1
3) вектора i, j, k образуют правую тройку
Три некомпланарных вектора a, b, с образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b.




 правая тройка левая тройка
правая тройка левая тройка
 с с
с с
 а b а b
а b а b
Свойства векторного произведения:
1) при перестановке сомножителей, векторное произведение меняет знак.
a×b  a×b = - b×a
a×b = - b×a



S Вектора a×b и b×a коллинеарны, имеют одинаковые модули (S
параллелограмма остается неизменной), но противоположно
 направлены.
направлены.
b×a
2) Векторное произведение обладает сочетательным свойством, относительно скалярного множителя.
λ(a×b) = (λ a)×b = (a×λ b)
Доказательство:
Пусть λ›0 ; λ(a×b) перпендикулярен а и b, вектор (λ a)×b также перпендикулярен а и b. Вектора а и λ a лежат в одной плоскости. Значит вектора λ(a×b) и (λ a)×b коллинеарны. Очевидно, что их направления совпадают, имеют одинаковую длину.
│λ(a×b) │= λ│a×b│=λ│а││b│sin(a,b)
│(λ a)×b│= │λ a││b│sin(λ a,b) = λ│a││b│sin(a,b)
Поэтому λ(a×b) = λ a×b
Аналогично доказывается при λ‹0
3) Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно ненулевому вектору, то есть:
а || b <=> a×
