ЗАДАЧИ К КОНТРОЛЬНОЙ РАБОТЕ № 1
1.01. Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением s = A + Bt2, где A = 8 м, В = - 2 м/с2. Определить момент времени t, когда нормальное ускорение аn точки равно 12 м/с2. Найти скорость υ, тангенциальное аτ и полное а ускорения точки в тот же момент времени t.
1.02. Две материальные точки движутся согласно уравнениям x1 = A1 t + + В1 t2 + С1 t3 и x2 = A2 t + В2 t2 + С2 t3, где A1 = 4 м/с, В1 = 8 м/с2, C1 = - 16м/с3, A2 = 2 м/с, В2 = - 4 м/с2 , С2= 1 м/с3. В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости υ1 и υ2 точек в этот момент.
1.03. Материальная точка движется в плоскости ху согласно уравнениям x = A1 + В1 t + С1 t2 и y = A2 + В2 t +С2 t2, где В1 = 7 м/с, C1 = - 2 м/с2, В2 = - 1 м/с, С2= 0,2 м/с2. Найти модули скорости и ускорения точки в момент времени t = 5 c.
1.04. Зависимость пройденного телом пути s от времени t дается уравнением
s = A + Bt + Ct2+ Dt3, где C = 0,14 м/с2 и D = 0,01 м/с3. Через какое время t после начала движения тело будет иметь ускорение а = 1 м/с2? Найти среднее ускорение тела за этот промежуток времени.
1.05. Шар массой m = 10 кг и радиусом R = 0,2 м вращается вокруг оси, проходящей через его центр. Закон движения шара имеет вид φ = А + B t2 + C t3, где В = 4 рад/с2, С = - 1 рад/с3. Найти зависимость момента сил, действующих на шар, от времени. Чему будет равен момент сил М в момент времени t = 2 с?
1.06. Маховик, момент инерции которого J = 50 кг•м2, вращается по закону: φ = А + B t + C t2, где А = 2 рад, В = 16 рад/с, С = - 2 рад/с2. Найти закон изменения вращающего момента М и закон изменения мощности N. Чему равна мощность N1 в момент времени t = 3 с?
1.07. Зависимость пройденного телом пути s от времени t дается уравнением s = A t – B t2+ C t3, где А = 2 м/с, В = 3 м/с2 и С = 4 м/с3. Найти: 1) зависимость скорости υ и ускорения а от времени t; 2) путь s, пройденный телом, скорость υ и ускорение а тела через время t = 2 с после начала движения.
1.08. Зависимость пройденного телом пути s от времени t дается уравнением s = A + B t + C t2, где А = 3 м, В = 2 м/с и C = 1 м/с2. Найти среднюю скорость и среднее ускорение тела за первую, вторую и третью секунды его движения.
1.09. Точка движется по прямой согласно закону х = A t + В t3, где А = 6 м/с; В = - 0,125 м/с3. Определить: 1) среднюю скорость точки в интервале времени от t1 = 2 с до t2 = 6 с; 2) координату точки в тот момент времени, когда скорость тела будет равна нулю.
1.10. Материальная точка совершает колебания по закону 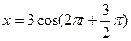 . Определить 1) период колебаний, 2) максимальную скорость, 3) максимальное ускорение точки.
. Определить 1) период колебаний, 2) максимальную скорость, 3) максимальное ускорение точки.
1.11. Тело брошено вертикально вверх с начальной скоростью υо = 4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью υо вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
1.12.Камень падает вертикально вниз с высоты 20 м. Начальная скорость равна нулю. Определите время падения камня, среднюю скорость падения камня.
1.13.Шарик бросают вертикально вверх со скоростью υо = 2 м/с с высоты h = 5 м. Определите 1) максимальную высоту подъема шарика; 2) время его падения на землю; 3) скорость в момент падения.
1.14.Два мяча бросают вертикально вверх из одной точки с одинаковыми скоростями 10 м/с с интервалом в 1 с. Определите, через какой промежуток времени после бросания первого мяча они встретятся в воздухе.
1.15. Пушка и цель находятся на одном уровне на расстоянии 5,1 км друг от друга. За какое время снаряд, выпущенный под произвольным углом к горизонту с начальной скоростью 240 м/с, достигнет цели? Сопротивлением воздуха пренебречь.
1.16. Камень, брошенный горизонтально, упал на землю через время t = 0,5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью υxон брошен?
1.17. Тело брошено под углом α = 30° к горизонту со скоростью υо = 30 м/с. Какова будет его скорость через время t = 1 с после начала движения?
1.18.Тело массой m = 0,5 кг брошено со скоростью υо = 10 м/с под углом α = 30° к горизонту. Пренебрегая сопротивлением воздуха, определите кинетическую T, потенциальную П и полную энергии тела: 1) через t = 0,4 c после начала движения; 2) в высшей точке траектории.
1.19. Какой начальной скоростью υо должна обладать сигнальная ракета, выпущенная под углом α = 45° к горизонту, чтобы она вспыхнула в наивысшей точке своей траектории? Время горения запала ракеты t = 6 c.
1.20. Вертолет летит горизонтально со скоростью υ = 160 км/ч на высоте h = 500 м. С вертолета нужно сбросить вымпел на остров. На каком по горизонтали расстоянии от острова летчик должен сбросить вымпел?
1.21. При горизонтальном полете со скоростью υ = 250 м/с, снаряд массой m = 8 кг разорвался на две части. Большая часть массой m1 = 6 кг получила скорость u1 = 400 м/с в направлении полета снаряда. Определить модуль и направление скорости u2 меньшей части снаряда.
1.22. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α = 30° к линии горизонта. Определить скорость u2 отката платформы, если снаряд вылетает со скоростью υ1 = 480 м/с. Масса платформы с орудием и снарядами m2= 18 т, масса снаряда m1 = 60 кг.
1.23. Конькобежец, стоя на коньках на льду, бросает камень массой m1 = 2,5 кг под углом α = 30° к горизонту со скоростью υ = 10 м/с. Какова будет начальная скорость υо движения конькобежца, если масса его m2 = 60 кг? Перемещением конькобежца во время броска пренебречь.
1.24. Человек массой m1 = 70 кг, бегущий со скоростью υ1 = 9 км/ч, догоняет тележку массой m2 = 190 кг, движущуюся со скоростью υ2 = 3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
1.25. Снаряд, летевший со скоростью υ = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40 % от массы снаряда, полетел в противоположном направлении со скоростью и1 = 150 м/с. Определить скорость u2 большего осколка.
1.26. В деревянный шар массой m1 = 8 кг, подвешенный на нити длиной l = 1,8 м, попадает горизонтально летящая пуля массой m2 = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3°? Размером шара пренебречь. Удар пули считать прямым, центральным.
1.27. Шар массой т1= 1кг движется со скоростью υ1= 4 м/с и сталкивается с шаром массой m2 = 2 кг, движущимся навстречу ему со скоростью υ2 = 3 м/с. Каковы скорости и1и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
1.28. Шар массой m1 = 5 кг движется со скоростью υ1 = 1 м/с и сталкивается с покоящимся шаром массой m2 = 2 кг. Определить скорости и1и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
1.29. Шар массой m1 = 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40 % кинетической энергии. Определить массу m2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
1.30. Из ружья массой m1 = 5 кг вылетает пуля массой m2 = 5 г со скоростью υ2 = 600 м/с. Найти скорость υ1 отдачи ружья.
1.31. Брусок массой m = 2 кг зажат между двумя вертикальными плоскостями с силой F = 10 Н. Найти ускорение бруска и силу трения между бруском и плоскостью при его проскальзывании. Какую минимальную вертикальную силу Fmin нужно приложить к бруску, чтобы поднимать его вверх? Определить работу этой силы на пути 20 см. Коэффициент трения μ = 0,5.
1.32. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами m1 =150 г и m2 = 100 г, которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите: 1) ускорение грузов; 2) силу натяжения нити T, 3) работу силы тяжести, действующей на первый груз при опускании его на 40 см.
1.33. Через легкий неподвижный блок перекинута невесомая нить с двумя грузами на концах, массы которых m1 = 200 г и m2 = 140 г. Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов и силу натяжения нити. Трение в оси блока отсутствует. Определить работу силы тяжести, действующей на второй груз при его подъеме на 25 см.
1.34. Если к телу, находящемуся на горизонтальной поверхности, приложить силу F = 120 Н под углом α = 60° к горизонту, то тело будет двигаться равномерно. Найти среднюю мощность силы трения, если 60 см тело проходит за 10 с.
1.35. Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами М. Одновременно на каждый из грузов кладут по перегрузку: справа -массой З m, слева – m. Определить ускорение системы и силу натяжения нити, если М = 200 г, m = 50 г. Определить работу силы натяжения нити на пути 35 см.
1.36.Тело массой m = 5 кг скользит по наклонной плоскости, составляющей с горизонтом угол α = 45°. Зависимость пройденного телом пути от времени t дается уравнением s = C t2, где С = 1,73 м/с2. Найти коэффициент трения тела о плоскость. Определить мощность в момент времени t = 2 мин.
1.37.На гладком столе лежит брусок массой m1 = 4 кг. К бруску привязан шнур, перекинутый через неподвижный блок. К концу шнура подвешена гиря массой m2 = 1 кг. Найти ускорение а, с которым движется брусок, и силу Т натяжения шнура. Массой блоков и трением пренебречь. Найти работу силы натяжения при передвижении гири на 0,5 м.
1.38.На столе стоит тележка массой m1 = 5 кг. К тележке привязан один конец шнура, перекинутого через блок. С каким ускорением a будет двигаться тележка, если к другому концу шнура привязать гирю массой m2 = 2 кг? Определить работу силы тяжести, действующей на гирю на пути 10 см.
1.39.Через блок перекинут шнур, к концам которого привязали грузы массами m1 = 1,5 кг и m2 = 3 кг. Какова будет сила натяжения нити во время движения грузов? Массой блока и шнура пренебречь. Определить работу силы тяжести, действующей на второй груз на пути 45 см.
1.40.Два бруска массами m1 = 1 кг и m2 = 4 кг, соединенные шнуром, лежат на столе. С каким ускорением а будут двигаться бруски, если к первому бруску приложить силу F = 10 Н, направленную горизонтально? Определить среднюю мощность этой силы за 3 с. Трением пренебречь.
1.41. Нить с привязанными к ее концам грузами массами т1 = 50 г и m2 = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение β = 1,5 рад/с2. Трением и проскальзыванием нити по блоку пренебречь.
1.42.Диск массой m = 2 кг катится без проскальзывания по горизонтальной плоскости со скоростью υ = 4 м/с. Найти кинетическую энергию Екдиска.
1.43. Маховик, момент инерции которого J = 63,6 кг•м2, вращается с постоянной угловой скоростью ω = 31,4 рад/с. Найти тормозящий момент, под действием которого маховик останавливается через t = 20 с.
1.44. Маховик радиусом R = 0,2 м и массой m = 10 кг соединен с мотором при помощи ремня. Сила натяжения ремня, идущего без скольжения, постоянна и равна Т = 14,7 Н. Какое число оборотов в секунду будет делать маховик через промежуток времени ∆t = 10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
1.45. К ободу колеса, имеющего форму диска, радиус которого R = 0,5 м и масса m = 50 кг, приложена касательная сила F = 100 Н. Найти: 1) угловое ускорение колеса β; 2) через какое время после начала действия силы колесо будет иметь частоту вращения n = 100 об/с.
1.46. Маховое колесо, имеющее момент инерции J = 24,5 кг•м2, вращается, делая n = 20 об/с. Через промежуток времени ∆t = 1 мин после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
1.47. Через неподвижный блок в виде сплошного диска перекинута нить, к концам которой привязаны грузы m1 = 100 г и m2 = 110 г. С каким ускорением будут двигаться грузы, если масса блока m = 400 г? Трением в блоке пренебречь.
1.48. Кинетическая энергия вращающегося маховика Ек= 1 кДж. Под действием тормозящего момента маховик начал вращаться равнозамедлено и, сделав N = 80 оборотов, остановился. Определить момент М силы торможения.
1.49. Маховик, момент инерции которого J = 40 кг•м2, из состояния покоя начал вращаться равноускоренно под действием момента силы М = 20 Н•м за t = 10 с. Определить кинетическую энергию Ек, приобретенную маховиком.
1.50. Маховое колесо начинает вращаться с постоянным угловым ускорением β = 0,5 рад/с2 и через t1 = 15 с после начала движения приобретает момент импульса L = 73,5 кг•м2/с. Найти кинетическую энергию колеса Екчерез t2= 20 с после начала движения.
1.51. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой т = 5кг каждая. Расстояние от каждой гири до оси скамьи l1= 70 см. Скамья вращается с частотой n1 = 1 с-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2 = 20 см? Момент инерции человека и скамьи (вместе) относительно оси J = 2,5 кг∙м2.
1.51. Три баллона вместимости которых соответственно равны V1 = 3 дм3, V2 = 7 дм3 , V3 = 5 дм3, наполнены один кислородом ( р1 = 2·105 Па ), другой -азотом ( р2 = 3·105 Па ) и третий - углекислым газом ( р3 = 6·104 Па ) при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
1.52. Два студента определяли плотность воздуха. Сначала они взвесили пустой сосуд и нашли, что его масса равна 20 г. Затем они надули мягкий сферический баллон из пластика до диаметра 21 см и выдавили его содержимое в сосуд. Масса сосуда с воздухом из баллона оказалась равной 26,5 г. Чему были равны плотность воздуха и его давление внутри баллона? Температура воздуха 20° С.
1.53. Определите плотность смеси водорода массой 4 г и кислорода массой 32 г при температуре 7° С и давлении 700 мм. рт. ст.
1.54. Плотность углекислотной (СО2) атмосферы Венеры примерно в 50 раз выше плотности земной атмосферы при нормальных условиях. Считая, что температура у поверхности Венеры 477° С, найдите венерианское атмосферное давление.
1.55. Когда в течение длительного времени автомобиль идет по шоссе, особенно летом, камеры и заполняющий их воздух нагреваются в результате деформаций и трения, а также от соприкосновения с нагретой поверхностью шоссе. На сколько процентов изменится давление в камере, если температура воздуха в камере повысится с 27° С до 30° С?
1.56. В сосуде вместимостью 1 л находится кислород массой 1 г. Определить концентрацию молекул кислорода в сосуде.
1.57. Сосуд содержит воздух при атмосферном давлении и температуре 20° С. До какой температуры нужно нагреть этот сосуд, чтобы из него вытиснилась одна пятая часть всех молекул, первоначально находившихся в сосуде?
1.58. В баллоне вместимостью 0,5 дм3 содержится смесь газов, состоящая из 1020 молекул кислорода, 4·1020 молекул азота и 3,3·1020 молекул аргона. Определите: 1) давление смеси; 2) молярную массу смеси. Температура смеси 127° С.
1.59. Баллон вместимостью 20 л наполнен сжатым воздухом. При температуре t1 = 20° С манометр показывает давление р1 = 1,2·107 Па. Какой объем воды можно вытеснить из цистерны подводной лодки воздухом этого баллона, если вытеснение производится на глубине h = 30 м и температура на этой глубине равна t2 = 15° С? Атмосферное давление ро= 105 Па.
1.60.В цилиндр длиной l = 1,6 м, заполненный воздухом при нормальном атмосферном давлении pо = 105 Па, начали медленно вдвигать поршень площадью S = 200 см2. Определить силу F, которая будет действовать на поршень, если его остановить на расстоянии l1 = 10 см от дна цилиндра.
1.61. При изотермическом расширении азота при температуре T = 280 К объем его увеличился в два раза. Определить: 1) совершенную при расширении газа работу А; 2) изменение внутренней энергии ΔU; 3) количество теплоты Q, полученное газом. Масса азота m = 0,2 кг.
1.62. Азот массой m = 0,1 кг был изобарно нагрет от температуры T1 = 200 К до температуры Т2 = 400 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение внутренней энергии азота ΔU.
1.63. Во сколько раз увеличится объем водорода, содержащий количество вещества v = 0,4 моль при изотермическом расширении, если при этом газ получит количество теплоты Q = 800 Дж? Температура водорода Т = 300 К.
1.64. Какая работа совершается при изотермическом расширении водорода массой m = 5 г, взятого при температуре Т = 290 К, если объем газа увеличивается в три раза? Определить полученное газом количество теплоты Q.
1.65. Определить работу, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты Q = 21 кДж. Найти также изменение внутренней энергии ΔU газа.
1.66. Азот массой m = 5 кг, нагретый на ΔT = 150 К, сохранил неизменный объем V. Найти: 1) количество теплоты Q, сообщенное газу; 2) изменение ΔU внутренней энергии; 3) совершенную газом работу A.
1.67. Водород занимает объем V1 = 10 м3 при давлении p1 = 100 кПа. Газ нагрели при постоянном объеме до давления p2 = 300 кПа. Определить: 1) изменение ΔU внутренней энергии газа; 2) работу А, совершаемую газом; 3) количество теплоты, сообщенное газу.
1.68. При изохорическом нагревании кислорода объемом V = 50 л давление газа изменилось на Δp = 0,5 МПа. Найти количество теплоты, сообщенное газу.
1.69. Идеальный газ, совершающий цикл Карно, 70% количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определить: 1) термический КПД цикла; 2) работу, совершаемую при полном цикле.
1.70.Водород нагревался при постоянном давлении, причем ему было сообщено количество теплоты Q = 42 кДж. Определить работу А, которую совершил при этом газ, и изменение ΔU его внутренней энергии.
1.71.Двухатомный газ, находящийся при давлении 2 МПа и температуре 27 0С, сжимается адиабатически, причем объем уменьшается вдвое. Найдите температуру и давление газа после сжатия.
1.72.При адиабатическом сжатии воздуха в цилиндре двигателя внутреннего сгорания давление изменяется от 0,1 МПа до 3,5 МПа. Начальная температура воздуха 25 0С. Найдите температуру воздуха после сжатия.
1.73.Газ расширяется адиабатически, причем объем увеличивается вдвое, а температура падает в 1,32 раза. Какое число степеней свободы имеют молекулы этого газа?
1.74.Кислород объемом 8 л адиабатически сжимается до объема 2 л, при этом в конце сжатия устанавливается давление2 МПа. Под каким давлением находился газ до сжатия и какова была его температура?
1.75.До какой температуры охладится воздух, находящийся при температуре 00С, если объем газа в результате адиабатического расширения увеличился втрое?
1.76.Двухатомный газ занимает объем 0,5 л при давлении 50 кПа. Газ адиабатически сжали, в результате чего объем его стал 100 мл. Найдите давление газа после сжатия и его температуру, если масса кислорода равна 0,4 г.
1.77.10 г кислорода нагревается от 50 до 200 0С. Найдите изменение энтропии, если нагревание происходит изохорически.
1.78.Найдите изменение энтропии и затраченную работу при изотермическом расширении 6 г водорода от 100 до 50 кПа.
1.79.28 кг азота, находящегося при нормальных условиях, расширяется адиабатически в 5 раз. Найдите изменение внутренней энергии газа и совершенную работу.
1.80.28 г азота, находящегося при температуре 25 0С и давлении 100 кПа сжимается адиабатически до объема 13 л. Найдите температуру и давление газа после сжатия и затраченную при этом работу.
Р А З Д Е Л II
ЭЛЕКТРОМАГЕНТИЗМ
ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ
| Физическая величина или закон | Формула |
| Закон Кулона (для точечных зарядов) |  |
| Напряженность электрического поля | E=F/q, где Е – напряженность электрического поля, F – сила, действующая на заряд q, помещенный в данное поле |
| Напряженность Е и потенциал φ поля, создаваемого точечным зарядом | 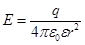 , , 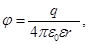 где– q – заряд, создающий поле, r – расстояние от заряда до заданной точки, где– q – заряд, создающий поле, r – расстояние от заряда до заданной точки, 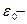 электрическая постоянная, электрическая постоянная, 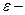 диэлектрическая проницаемость среды диэлектрическая проницаемость среды |
| Линейная плотность заряда | τ = q/l, τ = dq/dl, где τ – линейная плотность заряда, q – заряд, l – расстояние между зарядами |
| Поверхностная плотность заряда | σ=q/S, σ=dq/dS где σ – поверхностная плотность заряда, q – заряд, S – площадь поверхности |
| Объемная плотность заряда | ρ = q/V, ρ = dq/dV где ρ – объемная плотность заряда, q – заряд, V – некоторый объем |
| Поток вектора напряженности электрического поля | 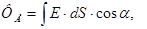 где dS – элемент площади поверхности, через которую определяется поток, α – угол между нормалью к данной поверхности и вектором где dS – элемент площади поверхности, через которую определяется поток, α – угол между нормалью к данной поверхности и вектором 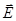 |
| Теорема Гаусса |  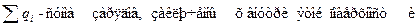 |
| Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью |  |
| Напряженность Поля внутри конденсатора | 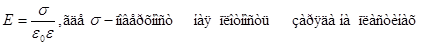 |
| Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром (нитью) |  |
| Работа сил поля по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2 | А12 = q (φ1-φ2), где А12 – работа сил по перемещению заряда, q – заряд, φ - потенциал |
| Электроемкость проводника | C=q/φ, где С – электроемкость проводника, q – заряд, φ - потенциал |
| Электроемкость плоского конденсатора | C = 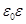 S/d, С=q/U, где C – электроемкость плоского конденсатора, S/d, С=q/U, где C – электроемкость плоского конденсатора, 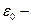 электрическая постоянная, S – площадь конденсатора, d – расстояние между пластинами конденсатора, U – разность потенциалов, электрическая постоянная, S – площадь конденсатора, d – расстояние между пластинами конденсатора, U – разность потенциалов, 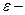 диэлектрическая проницаемость среды диэлектрическая проницаемость среды |
| Электроемкость батареи конденсаторов при последовательном соединении |  |
| Электроемкость батареи конденсаторов при параллельном соединении |  |
| Энергия заряженного конденсатора | W = qU/2, W=CU2/2, W=q2/(2C), где q – заряд конденсатора, U – разность потенциалов между обкладками, C – электроемкость конденсатора |
| Сила постоянного тока | I =q/t, I =dq/dt где I – сила тока, q – заряд, t - время |
| Плотность тока | j= I /S, где j – плотность тока, I – сила тока, S – площадь поперечного сечения проводника |
| Закон Ома для участка цепи, не содержащего ЭДС | 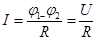 , где I - сила тока, , где I - сила тока, 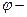 потенциал, U - напряжение, R - сопротивление потенциал, U - напряжение, R - сопротивление |
| Закон Ома для участка цепи, содержащего ЭДС |  |
| Закон Ома для замкнутой (полной) цепи | 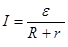 , где I – сила тока, , где I – сила тока, 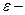 э.д.с., R – сопротивление, r – внутреннее сопротивление источника тока э.д.с., R – сопротивление, r – внутреннее сопротивление источника тока |
| Первый закон Кирхгофа | 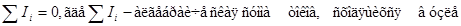 |
| Второй закон Кирхгофа | 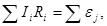 где Ii Ri – падение напряжения в замкнутом контуре, где Ii Ri – падение напряжения в замкнутом контуре, 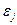 - ЭДС в данном контуре - ЭДС в данном контуре |
| Сопротивление проводников при последовательном соединении | 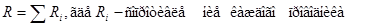 |
| Сопротивление проводников при параллельном соединении | 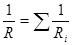 |
| Мощность тока | Р= IU, P = I 2R, P=U 2/R, где Р – мощность тока, I – сила тока, R – сопротивление, U - напряжение |
| Закон Джоуля-Ленца | dQ = I 2Rdt=IUdt, где dQ – тепло, выделяемое при нагревании проводника, I – сила тока, R – сопротивление, t – время, U - напряжение |
| Закон Ома и Джоуля-Ленца в дифференциальной форме | j=γE, ω= γE2 где j – плотность тока, γ – удельная электрическая проводимость, Е - напряженность электрического поля, ω – объемная плотность мощности |
| Связь магнитной индукции Вс напряженностью Н магнитного поля | B=mm0H, где В – магнитная индукция, Н – напряженность магнитного поля, μ – магнитная проницаемость среды, µ0 – магнитная постоянная |
| Закон Био-Савара-Лапласа | 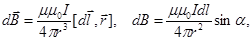 где где 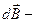 индукция поля, µ - магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, индукция поля, µ - магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, 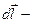 вектор, равный по модулю длине проводника, вектор, равный по модулю длине проводника, 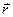 – радиус-вектор, проведенный из проводника в точку поля, α – угол между векторами – радиус-вектор, проведенный из проводника в точку поля, α – угол между векторами 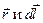 |
| Магнитная индукция прямого бесконечно длинного проводника с током | 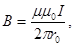 где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, r0 – расстояние от проводника с током до точки, в которой определяется индукция магнитного поля где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, r0 – расстояние от проводника с током до точки, в которой определяется индукция магнитного поля |
| Магнитная индукция поля в центре кругового проводника с током | 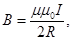 где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, R – радиус проводника где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, R – радиус проводника |
| Магнитная индукция поля внутри соленоида | 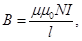 где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, N – количество витков, l – длина соленоида где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, N – количество витков, l – длина соленоида |
| Энергия магнитного поля соленоида | 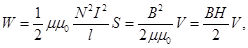 где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, N – количество витков, l – длина соленоида, S – площадка, через которую проходит магнитный поток, В – магнитная индукция, V – объем соленоида, Н – напряженность магнитного поля где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, N – количество витков, l – длина соленоида, S – площадка, через которую проходит магнитный поток, В – магнитная индукция, V – объем соленоида, Н – напряженность магнитного поля |
| Сила, действующая на провод с током в магнитном поле (закон Ампера) | F = I B l sin α, 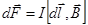 , где F – сила, I – сила тока, В – магнитная индукция, l – длина провода, α – угол между векторами , где F – сила, I – сила тока, В – магнитная индукция, l – длина провода, α – угол между векторами 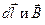 |
| Магнитный момент плоского контура с током | 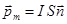 , где I – сила тока, S – площадь контура, , где I – сила тока, S – площадь контура, 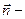 нормальный вектор нормальный вектор |
| Сила Лоренца | F = q υ B sin α, где q – заряд, υ – скорость заряда, В – магнитная индукция, α – угол между векторами 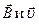 |
| Магнитный поток в случае однородного магнитного поля и плоской поверхности | Ф = B S cos α , Ф = Bn S, где Ф – магнитный поток, B - магнитная индукция, S – площадь поверхности, α – угол между векторами 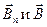 , Вn – проекция вектора , Вn – проекция вектора 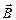 на направление нормали к площадке S на направление нормали к площадке S |
| Работа по перемещению проводника с током в магнитном поле | dA = IdФ, где A – работа по перемещению проводника, Ф – магнитный поток, I – сила тока |
| ЭДС индукции | 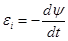 , где , где 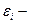 ЭДС индукции, ψ – полный магнитный поток, t - время ЭДС индукции, ψ – полный магнитный поток, t - время |
| ЭДС самоиндукции | 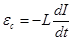 , где , где 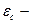 ЭДС самоиндукции, L – индуктивность, I – сила тока, t - время ЭДС самоиндукции, L – индуктивность, I – сила тока, t - время |
| Индуктивность соленоида | L =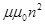 V, где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, V – объем соленоида, n – плотность намотки V, где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, V – объем соленоида, n – плотность намотки |
| Экстратоки при замыкании и размыкании цепи | 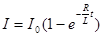 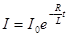 I0 – сила тока в начальный момент времени, R - активное сопротивление цепи, L - индуктивность I0 – сила тока в начальный момент времени, R - активное сопротивление цепи, L - индуктивность |
| Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему) | w = В2/(2 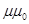 ), w = ), w = 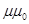 Н2/2, w = BН/2, где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, B - магнитная индукция, Н – напряженность магнитного поля Н2/2, w = BН/2, где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, B - магнитная индукция, Н – напряженность магнитного поля |
| Теорема Гаусса для электростатического поля в диэлектрике | 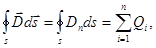 где где 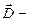 вектор электрического смещения, s – произвольная замкнутая поверхность, Dn – проекция вектора вектор электрического смещения, s – произвольная замкнутая поверхность, Dn – проекция вектора 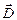 на нормаль к площадке s, на нормаль к площадке s, 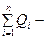 алгебраическая сумма свободных зарядов, заключенных внутри данной замкнутой поверхности алгебраическая сумма свободных зарядов, заключенных внутри данной замкнутой поверхности |
| Закон полного тока для магнитного поля | 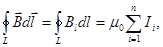 где где 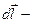 вектор элементарной длины контура, вектор элементарной длины контура, 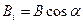 ( ( 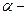 угол между векторами угол между векторами 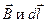 ), ), 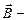 вектор магнитной индукции, μ0 – магнитная постоянная, вектор магнитной индукции, μ0 – магнитная постоянная, 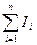 — алгебраическая сумма токов, охватываемых контуром, n — число токов. — алгебраическая сумма токов, охватываемых контуром, n — число токов. |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.Два точечных заряда 9Q и -Q закреплены на расстоянии l = 50 см друг от друга. Третий заряд Q1может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q1, при котором он будет находиться в равновесии. При каком знаке заряда Q1равновесие будет устойчивым?
Решение. Заряд Q1находится в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Это значит, что на заряд Q1должны действовать две силы, равные по модулю и противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (Рис. 4) может быть выполнено это условие. Для определенности будем считать, что заряд Q1— положительный.
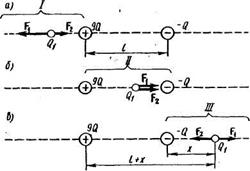
Рис. 5.
На участке I (рис. 5, а) на заряд Q1будут действовать две противоположно направленные силы: 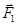 и
и 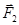 . Сила
. Сила 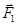 , действующая со стороны заряда 9Q, в любой точке этого участка больше силы
, действующая со стороны заряда 9Q, в любой точке этого участка больше силы 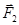 , действующей со стороны заряда
, действующей со стороны заряда
-Q, так как больший заряд 9Q находится всегда ближе к заряду Q1, чем меньший (по модулю) заряд -Q. Поэтому равновесие на этом участке невозможно.
На участке II (рис. 4, б) обе силы 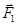 и
и 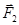 направлены в одну сторону — к заряду -Q. Следовательно, и на втором участке равновесие невозможно.
направлены в одну сторону — к заряду -Q. Следовательно, и на втором участке равновесие невозможно.
На участке III (рис. 4, в) силы 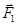 и
и 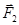 направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд -Q всегда находится ближе к заряду Q1,чем больший заряд 9Q. Это значит, что можно найти такую точку на прямой, где силы
направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд -Q всегда находится ближе к заряду Q1,чем больший заряд 9Q. Это значит, что можно найти такую точку на прямой, где силы 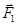 и
и 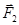 будут одинаковы по модулю, т. е.
будут одинаковы по модулю, т. е.
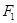 =
= 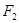 (1)
(1)
Пусть х и l+х — расстояние от меньшего и большего зарядов до заряда Q1.Выражая в равенстве (1) 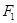 и
и 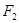 в соответствии с законом Кулона, получим
в соответствии с законом Кулона, получим
9Q Q1(l + x)2= Q Q1/x2, или l + x = ± Зх, откуда
x1 = + l/2,
x2= - l/4.
Корень x2не удовлетворяет физическому условию задачи (в этой точке силы 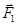 и
и 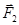 хотя и равны по модулю, но сонаправлены).
хотя и равны по модулю, но сонаправлены).
Определим знак заряда Q1, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение заряда Q1 в двух случаях: когда заряд положителен и когда отрицателен.
Если заряд Q1положителен, то при смещении его влево обе силы 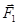 и
и 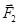 возрастают. Так как сила
возрастают. Так как сила 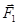 возрастает медленнее, то результирующая сила, действующая на заряд Q1, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд Q1 будет удаляться от положения равновесия. То же происходит и при смещении заряда Q1вправо. Сила
возрастает медленнее, то результирующая сила, действующая на заряд Q1, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд Q1 будет удаляться от положения равновесия. То же происходит и при смещении заряда Q1вправо. Сила 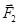 убывает быстрее, чем
убывает быстрее, чем 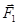 . Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
. Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
Если заряд Q1отрицателен, то его смещение влево вызовет увеличение сил 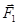 и
и 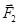 , но сила
, но сила 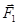 возрастает медленнее, чем
возрастает медленнее, чем 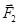 , т. е. |
, т. е. | 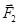 |>|
|>| 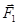 |. Результирующая сила будет направлена вправо. Под ее действием заряд Q1 возвращается к положению равновесия. При смещении Q1 вправо сила
|. Результирующая сила будет направлена вправо. Под ее действием заряд Q1 возвращается к положению равновесия. При смещении Q1 вправо сила 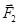 убывает быстрее, чем
убывает быстрее, чем 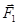 , т. е. |
, т. е. | 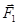 |>|
|>| 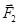 |. результирующая сила направлена влево и заряд Q1 опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q1несущественна.
|. результирующая сила направлена влево и заряд Q1 опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q1несущественна.
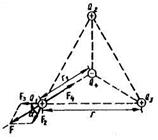
Рис. 6.
Задача 2. Три точечных заряда Q1 = Q2 = Q3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например Q1,находился и равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулевому вектору (Рис. 6):
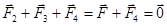 (1)
(1)
где 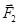 ,
, 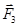 ,
, 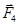 — силы, с которыми соответственно действуют на заряд Q1 заряды Q2, Q3, Q4;
— силы, с которыми соответственно действуют на заряд Q1 заряды Q2, Q3, Q4; 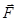 равнодействующая сил
равнодействующая сил 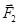 и
и 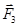
Так как силы 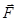 и
и 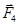 направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F - F4 = 0, откуда F4 = F. Выразив в последнем равенстве F через F2, F3 и учитывая, что F3 = F2, получим
направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F - F4 = 0, откуда F4 = F. Выразив в последнем равенстве F через F2, F3 и учитывая, что F3 = F2, получим
F4 = F2 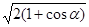 .
.
Применив закон Кулона и имея в виду, что Q2 = Q3 = Q1, найдем
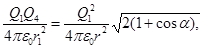
откуда Q4= 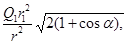 (2)
(2)
 Из геометрических построений в равностороннем треугольнике следует, что
Из геометрических построений в равностороннем треугольнике следует, что
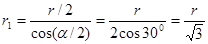 , cos α=cos 60°=l/2.
, cos α=cos 60°=l/2.
С учетом этого формула (2) примет вид
Q4 = Q1 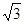 .
.
Произведем вычисления:
Q4 = 10-9 / 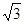 Кл = 5,77·10-10 Кл = 577 пКл.
Кл = 5,77·10-10 Кл = 577 пКл.
Задача 3. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд Q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне.
Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Q1зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ.
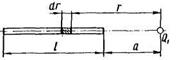
Рис. 7
При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (Рис. 7) малый участок dr с зарядом dQ = τdr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,
d F = 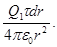
Интегрируя это выражение в пределах от a до a + l, получаем
F = 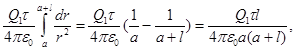
откуда 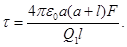
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:
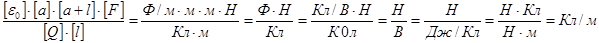
Найденная единица является единицей линейной плотности заряда.
Произведем вычисления:
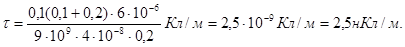
Задача 4. Два точечных электрических заряда Q1 = 1 нКл и Q2= - 2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Определить напряженность 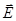 и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1на расстояние r1= 9 см и от заряда Q2 на r2 = 7 см.
и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1на расстояние r1= 9 см и от заряда Q2 на r2 = 7 см.
Решение. Согласно принципу суперпозиции электрических полей, поле, созданное зарядом, не зависит от присутствия других зарядов. Поэтому напряженность 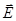 электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей 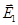 и
и 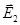 полей, создаваемых каждым зарядом в отдельности:
полей, создаваемых каждым зарядом в отдельности: 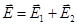 . Напряженности электрического поля, создаваемого в воздухе (ε = 1) зарядами Q1 и Q2, складываются.
. Напряженности электрического поля, создаваемого в воздухе (ε = 1) зарядами Q1 и Q2, складываются.
Вектор 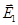 (Рис. 8.) направлен по силовой линии от заряда Q1, так как этот заряд положителен; вектор
(Рис. 8.) направлен по силовой линии от заряда Q1, так как этот заряд положителен; вектор 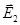 направлен также по силовой линии, но к заряду Q2 так как этот заряд отрицателен.
направлен также по силовой линии, но к заряду Q2 так как этот заряд отрицателен.
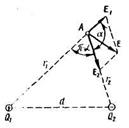
Рис. 8.
Модули векторов 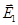 и
и 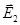 находим по формулам
находим по формулам
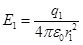 , (1)
, (1)
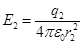 . (2)
. (2)
Модуль результирующего вектора 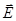 найдем по теореме косинусов:
найдем по теореме косинусов:
Е = 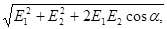 (3)
(3)
где α - угол между векторами 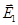 и
и 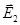 , который может быть найден из треугольника со сторонами r1, r2и d: cos α =
, который может быть найден из треугольника со сторонами r1, r2и d: cos α = 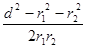 . В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:
. В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:
cos α = 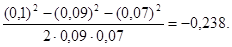
Подставляя выражение Е1 из (1) и Е2 из (2) в (3) и вынося общий множитель 1/(4 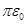 ) за знак корня, получаем
) за знак корня, получаем
Е = 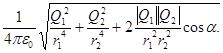 (4)
(4)
В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, создаваемого двумя зарядами Q1 и Q2, равен алгебраической сумме потенциалов;
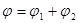 (5)
(5)
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
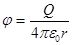 . (6)
. (6)
В нашем случае согласно формулам (5) и (6) получим
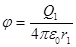 +
+ 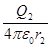 ,
,
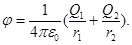
Произведем вычисления:
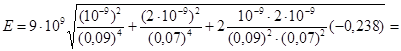
=3,58·103 В/м = 3,58 кВ/м;
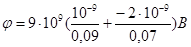 =-157 В.
=-157 В.
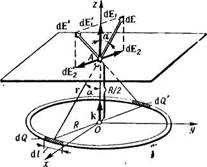
Рис. 9
Задача 5. По тонкому кольцу равномерно распределен заряд Q = 40 нКл с линейной плотностью τ = 50 нКл/м. Определить напряженность 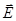 электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
Решение. Совместим координатную плоскость хoу с плоскостью кольца, а ось oz - с осью кольца (Рис. 9). На кольце выделим малый участок длиной dl. Так как заряд dQ = τ dl, находящийся на этом участке, можно считать точечным, то напряженность d 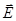 электрического поля, создаваемого этим зарядом, может быть записана в виде
электрического поля, создаваемого этим зарядом, может быть записана в виде
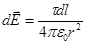 ,
,
где r— радиус-вектор, направленный от элемента dl к точке А.
Разложим вектор d 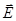 на две составляющие: d
на две составляющие: d 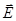 1, перпендикулярно плоскости кольца (сонаправленную с осью Oz), и d
1, перпендикулярно плоскости кольца (сонаправленную с осью Oz), и d 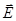 2, параллельную плоскости кольца (плоскости хoу), т. е.
2, параллельную плоскости кольца (плоскости хoу), т. е.
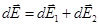
Напряженность Е электрического поля в точке А найдем интегрированием
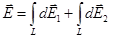 ,
,
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов (dQ = dQ'), расположенных симметрично относительно центра кольца, векторы 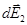 и
и 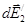 в точке А равны по модулю и противоположны по направлению:
в точке А равны по модулю и противоположны по направлению: 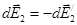 .Поэтому векторная сумма (интеграл)
.Поэтому векторная сумма (интеграл) 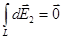 .
.
Составляющие 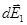 для всех элементов кольца сонаправлены с осью oz (единичным вектором
для всех элементов кольца сонаправлены с осью oz (единичным вектором 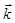 , определяющим направление оси Z), т.е.
, определяющим направление оси Z), т.е. 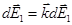 . Тогда
. Тогда
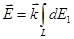 .
.
Так как dE = 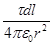 , r =
, r = 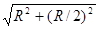 = =
= = 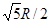 и cos α = (R/2 )/r = l/
и cos α = (R/2 )/r = l/ 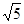 , то
, то
dE1 = 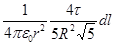 =
= 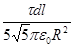 .
.
Таким образом
.
Из соотношения Q = 2πRτ определим радиус кольца: R = Q/(2πτ). Тогда
.
Модуль напряженности 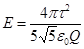 . (1)
. (1)
Проверим, дает ли правая часть полученного равенства единицу напряженности (В/м):
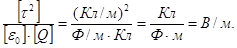
Выразим физические величины, входящие в формулу (1), в единицах СИ ( 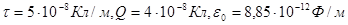 ) и произведем вычисления:
) и произведем вычисления:
Е = 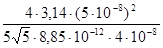 В/м = 7,94 кВ/м.
В/м = 7,94 кВ/м.
Задача 6.Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут соответственно заряды Q1 = 1 нКл и Q2 = -0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра сфер на расстояниях r1= 5 см, r2 = 9 см, r3 = 15 см ). Построить график Е(r).
