Энергия модели энергия поступ. энергия вращат

Движущ.звеньев движущ.звеньев

Приведение масс основано на равенстве кинетических энергий реальных звеньев и звена приведения одномассовой модели.

Если требуется определить какую-либо составляющую 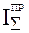, например 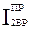, то записывают равенство:

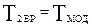
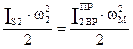
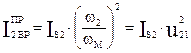
2.4.2 Приведение сил.

А_Σ –работа суммарного приведенного момента на его возможное перемещение.

Т – Т_нач = А_Σ

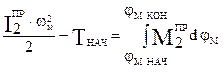
(1)

Приведение сил основано на равенстве секундных работ (мощностей) реальных сил и моментов, приложенных к звеньям механизма, на их возможных перемещениях и суммарного приведенного момента, приложенного к звену приведения, на его возможное перемещение.

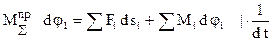
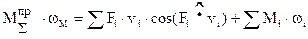
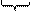
Передат передаточ

Функция отношение

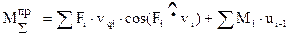
Вместо силы 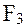– момент .

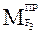Если необходимо определить какую-либо составляющую суммарного приведенного момента, например 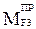, то необходимо записать равенство:

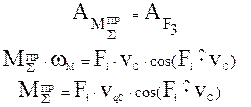
Вывод формулы для определения закона движения звена приведения в форме кинетической энергии (определение ω_м).

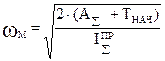где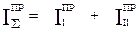

Const var

Режимы работы машинного агрегата.

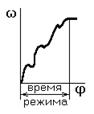
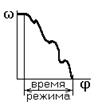
а) разгон б) торможение (выбег)

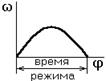в) безударный останов г) установившееся движение

рис. 2.6

а),б),в) – неустановившийся режим;

г) – установившийся режим.

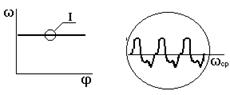
Определение законов движения для установившегося режима работы .

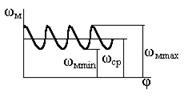
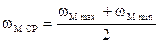
Отклонения угловой скорости от среднего уровня характеризуется коэффициентом неравномерности d

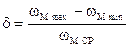
Коэффициент d определяется экспериментально и для различных машин имеет значения:

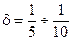машины ударного действия (прессы, молоты)

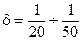полиграфические машины (насосы)

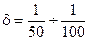электрогенераторы переменного тока

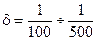электрогенераторы постоянного тока

Если рассчитанный действительный коэффициент неравномерности оказывается больше допустимого для данной машины, требуется постановка на звено приведения дополнительной массы- маховика. Он за счет своей инерционности будет выравнивать угловую скорость звена приведения. Для того чтобы удерживать колебания угловой скорости w_м в заданных пределах, определяемых коэффициентом неравномерности d, первая группа звеньев должна иметь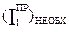

Изменение w_м от w_{м_max} до w_{м_min} приводит к изменению кинетической энергии первой группы звеньев (ΔТ_I), которое равно:

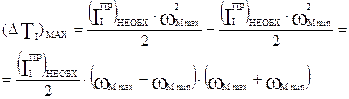
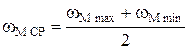
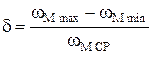
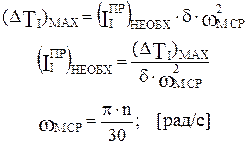
Это значение приведенного момента инерции и есть момент инерции маховика.

Трение является сложным физико-химическим процессом, сопровождающийся выделением тепла. Это вызвано тем, что перемещающиеся тела оказывают сопротивление относительному движению. Мерой интенсивности сопротивления относительному перемещению является сила (момент) трения.

Различают трение качения, трение скольжения, а также сухое, граничное и жидкостное трение.

Если суммарная высота микронеровностей взаимодействующих поверхностей:

· больше, чем высота слоя смазки, то - сухое трение.

· равна высоте слоя смазки, то -граничноетрение.

· меньше, чем высота слоя смазки, то - жидкостное .

Учет трения в поступательной кинематической паре.

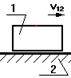Без учета трения реакция направлена по нормали к взаимодействующим поверхностям. При учете трения результирующая реакция Q₂₁ отклоняется от общей нормали на угол трения j в сторону противоположную направлению движения.

без учета трения с учетом трения

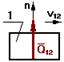
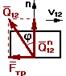F_тр=Qⁿ₁₂^.tg j

tg j= f

F_тр=Qⁿ₁₂^.f

Коэффициент трения f определяется экспериментально и зависит от многих факторов: материала, чистоты обработки поверхностей, наличия смазки.

Учет трения во вращательной кинематической паре.

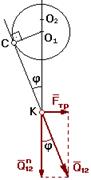
1 - цапфа

r_ц - радиус цапфы

Δ - зазор

r - радус круга трения;

r = О₁С

Из ΔО₁СК à 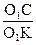= sin j à О₁С = О₁К sin j

M_c= Q₁₂^.О₁С = Q₁₂^. r_ц^.sin j

При малых углах j sin j ≈ tg j = f . Тогда :

M_c= Q₁₂^. r_ц^.f

При учете трения во вращательной КП результирующая реакция отклоняется от общей нормали на угол трения j и проходит касательно к кругу трения радиуса r

Эвольвента и ее свойства.

Эвольвента образуется путем перекатывания производящей прямой K_yN_y без скольжения по основной окружности радиуса r_b.

Радиус произвольной окружности – r_y. ON_y || tt

Из треугольника ON_yK_y следует, что

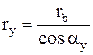(1)

Т.к. K_yN_y перекатывается без скольжения по основной окружности, то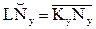

r_b(q_y + a_y) = r_b^.tg a_y

q_y = tg a_y - a_y (2)

q_y = inv a_y

q_y – инволюта;

Уравнения (1) И (2) являются уравнениями эвольвенты в параметрической форме.

a_у – угол профиля эвольвенты для точки К_у, лежащей на произвольной окружности.

a – угол профиля эвольвенты для точки К, лежащей на делительной окружности радиуса r.

Угол профиля эвольвенты для точки К_b, лежащей на основной окружности, равен нулю: a_b=0.

Свойства эвольвенты.

1. Форма эвольвенты зависит от радиуса основной окружности. При стремлении r_b 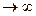,эвольвента превращается в прямую линию (пример рейка).

2. Производящая прямая K_yN_y является нормалью к эвольвенте в данной тоске.

3. Эвольвента начинается от основной окружности. Внутри основной окружности точек эвольвенты нет.

Элементы эвольвентного зубчатого колеса.

Делительной окружностью называется окружность стандартных шага р, модуля m и угла профиля a.

Шаг – расстояние между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.

Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:

1 ряд – наиболее предпочтительный;

2 ряд – средней предпочтительности;

3 ряд – наименее предпочтительный.

Модуль характеризует высоту зуба. Чем больше зуб, тем более шумной становится зубчатая передача.

Угол профиля – угол между касательной к эвольвенте в данной точке и радиус-вектором данной точки (см. чертеж эвольвенты).

Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20^о(хотя лучше 25^о).

Основные расчетные зависимости для определения параметров эвольвентного зубчатого колеса.

Из (1) следует, что радиус делительной окружности

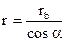
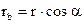(3)

модуль по ГОСТу определяется

m = p / p p = p^.m (4)

2p ^.r = p^.z

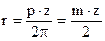(5)

2p ^.r_y = p_y^.z

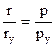à

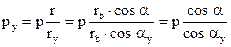
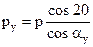(6)

Шаг по основной окружности

a_y = 0 à p_b = p cos 20^o (7)

Шаг по делительной окружности p = s + e (8)

Толщина зуба s= 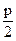+ Δ^.m (9)

где Δ – коэффициент изменения толщины зуба.

Виды зубчатых колес.

В зависимости от знака коэффициента Δ различают виды зубчатых колес:

1. Δ = 0 s = e = p/2 нулевое зубчатое колесо;

2. Δ > 0 s > e положительное зубчатое колесо;

3. Δ < 0 s < e отрицательное зубчатое колесо.

Эвольвентная зубчатая передача и ее свойства .

Эвольвентную зубчатую передачу составляют, как минимум, из 2-х зубчатых колес, при этом в рассмотрение вводится две начальные окружности радиусами r_w1 и r_w2.

Меньшее зубчатое колесо в обычной понижающей зубчатой передаче называется шестерня.

Вместо производящей прямой здесь вводится в рассмотрение линия зацепления N₁N₂, которая одновременно касается 2-х основных окружностей r_b1 и r_b2.

Линия зацепления является геометрическим местом точек контакта сопряженных эвольвентных профилей. В точке В₁ пара эвольвент, которые в данный момент времени контактируют в точке К, входят в зацепление. В точке В₂ этаже пара эвольвент из зацепления выходят.

На линии зацепления N₁N₂ все взаимодействующие эвольвенты при зацеплении касаются друг друга. Вне участка N₁N₂ эвольвенты пересекаются, и если такое случится, то произойдет заклинивание зубчатого колеса.

Угол N₁O₁P = N₂J₂P = a_w – угол зацепления.

Для передачи, составленной из нулевых зубчатых колес a_w=20^o

Для передачи, составленной из положительных з. к. a_w>20^o

Для передачи, составленной из отрицательных з. к. a_w<20^o

c=c*^.m - радиальный зазор, величина стандартная, необходим для нормального обеспечения смазки.

c* - коэффициент радиального зазора, по ГОСТ c*=0.25 (c*=0.35).

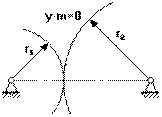
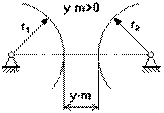
Между делительными окружностями у^.m – это воспринимаемое смещение.

у – коэффициент воспринимаемого смещения, он имеет знак, и в зависимости от знака различают:

1. у=0 у^.m=0 – нулевая зубчатая передача;

2. у>0 у^.m>0 – положительная зубчатая передача;

3. у<0 у^.m<0 – отрицательная зубчатая передача;

Свойства эвольвентного зацепления.

1. Эвольвентное зацепление молочувствительно к погрешностям изготовления, т.е. при отклонении межосевого расстояния от номинала передаточное отношение зубчатой передачи не изменится.

2. Линия зацепления N₁N₂ является общей нормалью к сопряженным эвольвентным профилям.

3. Контакт эвольвент осуществляется только на линии зацепления.

Качественные показатели зубчатых передач.

к ним относятся:

1. Коэффициент перекрытия e_a.

Характеризует плавность работы зубчатой передачи и показывает, какое число зубьев одновременно участвуют в перекрытии зацепления (насколько одна пара зубьев перекрывает работу другой).

Теоретически e_a может равен 1, и это означает, что как только одна пара зубьев вышла из зацепления, следующая пара сразу же вошла в зацепление.

Если e_a<1, то предыдущая пара зубьев из зацепления вышла, а следующая пара в зацепление не вошла. Такая передача работает с ударами, и ее применение недопустимо. Поэтому конструкторы при проектировании передачи считают минимально допустимым e_a равным 1.05 .

Как правило, эвольвентная зубчатая передача с прямозубыми колесами имеет коэффициент перекрытия e_a=1.1 – 1.5. Для косозубых колес за счет осевого перекрытия зубьев e_b=e_a+e_g, e_g 1 à e_b=2.1 – 2.5

Зубчатая передача с косозубыми колесами работает более плавно.