Тема: Динамика поступательного движения 4 страница
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Динамика вращательного движения
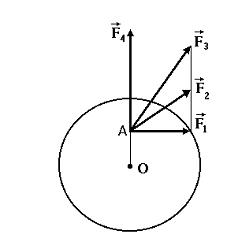
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил ( 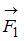 ,
, 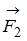 ,
, 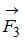 или
или 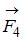 ), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение …
), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение …
 |  | 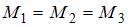 , , 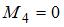 | |
 | 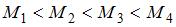 | ||
 | 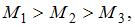 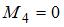 | ||
 | 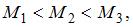 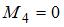 |
Решение:
При вращении тела вокруг неподвижной оси момент относительно этой оси создает только одна составляющая действующей на него силы, а именно касательная к траектории точки ее приложения 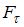 . Тогда момент силы относительно неподвижной оси равен:
. Тогда момент силы относительно неподвижной оси равен: 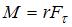 , где r – радиус-вектор точки приложения силы. В данном случае составляющая
, где r – радиус-вектор точки приложения силы. В данном случае составляющая 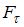 одинакова для трех сил:
одинакова для трех сил: 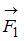 ,
, 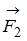 и
и 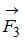 , а для силы
, а для силы 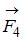
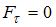 . Кроме того, все силы приложены в одной точке. Поэтому
. Кроме того, все силы приложены в одной точке. Поэтому 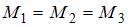 ,
, 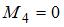 .
.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Кинематика поступательного и вращательного движения
Частица из состояния покоя начала двигаться по дуге окружности радиуса 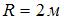 с угловой скоростью, модуль которой изменяется с течением времени по закону
с угловой скоростью, модуль которой изменяется с течением времени по закону 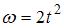 . Отношение нормального ускорения к тангенциальному через 2 секунды равно …
. Отношение нормального ускорения к тангенциальному через 2 секунды равно …
 |  | ||
 | |||
 | |||
 |
Решение:
Нормальное ускорение частицы равно 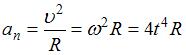 , где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением
, где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением 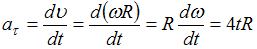 . Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно
. Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно 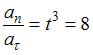 .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Элементы специальной теории относительности
Космический корабль летит со скоростью 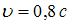 (
( 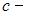 скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения наблюдателя, находящегося на планете, …
скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения наблюдателя, находящегося на планете, …
 |  | изменяется от 1,0 м в положении 1 до 0,6 м в положении 2 | |
 | изменяется от 1,0 м в положении 1 до 1,67 м в положении 2 | ||
 | равна 1,0 м при любой его ориентации | ||
 | изменяется от 0,6 м в положении 1 до 1,0 м в положении 2 |
Решение:
Движение макроскопических тел со скоростями, соизмеримыми со скоростью света в вакууме, изучается релятивистской механикой. Одним из следствий преобразований Лоренца является так называемое Лоренцево сокращение длины, состоящее в том, что линейные размеры тела сокращаются в направлении движения: 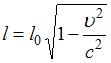 . Здесь
. Здесь 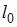 – длина тела в системе отсчета, относительно которой тело неподвижно;
– длина тела в системе отсчета, относительно которой тело неподвижно; 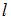 – длина тела в системе отсчета, относительно которой тело движется со скоростью
– длина тела в системе отсчета, относительно которой тело движется со скоростью 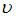 . При этом поперечные размеры тела не изменяются. Вычисления по приведенной формуле приводят к следующему результату:
. При этом поперечные размеры тела не изменяются. Вычисления по приведенной формуле приводят к следующему результату: 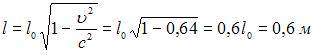 . Таким образом, длина стержня с точки зрения наблюдателя, находящегося на планете, изменяется от 1,0 м в положении 1 до 0,6 м в положении 2.
. Таким образом, длина стержня с точки зрения наблюдателя, находящегося на планете, изменяется от 1,0 м в положении 1 до 0,6 м в положении 2.
 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Динамика вращательного движения
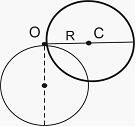
Диск радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 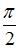 и отпустили. В начальный момент времени угловое ускорение диска равно _______
и отпустили. В начальный момент времени угловое ускорение диска равно _______ 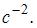
 |  | ||
 | |||
 | |||
 |
Решение:
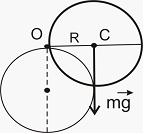
Момент силы тяжести относительно оси, проходящей через точку О, равен 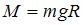 , где
, где 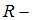 радиус диска и плечо силы. Момент инерции диска относительно оси, проходящей через центр тяжести (точку С), равен
радиус диска и плечо силы. Момент инерции диска относительно оси, проходящей через центр тяжести (точку С), равен 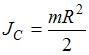 ; а момент инерции обруча относительно оси, проходящей через точку О, найдем по теореме Штейнера:
; а момент инерции обруча относительно оси, проходящей через точку О, найдем по теореме Штейнера: 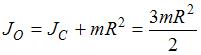 . Используя основной закон динамики вращательного движения твердого тела вокруг неподвижной оси, можем определить угловое ускорение:
. Используя основной закон динамики вращательного движения твердого тела вокруг неподвижной оси, можем определить угловое ускорение: 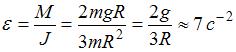 .
.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Работа. Энергия
Потенциальная энергия частицы в некотором силовом поле задана функцией 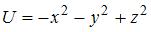 . Работа потенциальной силы (в Дж) по перемещению частицы из точки В (1, 1, 1) в точку С (2, 2, 2) равна …
. Работа потенциальной силы (в Дж) по перемещению частицы из точки В (1, 1, 1) в точку С (2, 2, 2) равна …
(Функция 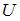 и координаты точек заданы в единицах СИ.)
и координаты точек заданы в единицах СИ.)
3  |
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Кинематика поступательного и вращательного движения
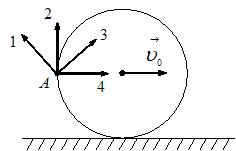
Диск катится равномерно по горизонтальной поверхности со скоростью 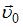 без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
 |  | ||
 | |||
 | |||
 |
Решение:
Качение однородного кругового цилиндра (диска) по плоскости является плоским движением. Плоское движение можно представить как совокупность двух движений: поступательного, происходящего со скоростью 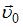 центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда
центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда 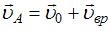 . Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что
. Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что 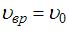 . Вектор
. Вектор 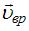 направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости
направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости 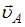 точки А ориентирован в направлении 3.
точки А ориентирован в направлении 3.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Динамика поступательного движения
Автомобиль поднимается в гору по участку дуги с увеличивающейся по величине скоростью.
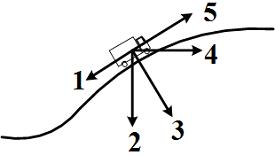
Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении …
4 |  |
Решение:
Согласно второму закону Ньютона 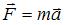 , где
, где 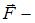 равнодействующая всех сил, действующих на тело,
равнодействующая всех сил, действующих на тело, 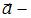 его ускорение. Вектор ускорения удобно разложить на две составляющие:
его ускорение. Вектор ускорения удобно разложить на две составляющие: 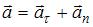 . Тангенциальное ускорение
. Тангенциальное ускорение 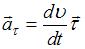 направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение
направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение 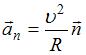 направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории
направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории 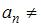 0, при движении с увеличивающейся по величине скоростью
0, при движении с увеличивающейся по величине скоростью 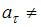 0 и вектор
0 и вектор 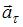 ориентирован в направлении 5. Следовательно, вектор
ориентирован в направлении 5. Следовательно, вектор 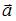 , а значит, и вектор
, а значит, и вектор 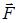 ориентирован в направлении 4.
ориентирован в направлении 4.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Законы сохранения в механике
Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии 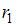 друг от друг, как показано на рисунке:
друг от друг, как показано на рисунке: 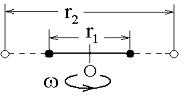
Стержень вращается без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками, с угловой скоростью 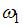 . Если шарики раздвинуть симметрично на расстояние
. Если шарики раздвинуть симметрично на расстояние  , то угловая скорость
, то угловая скорость 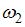 будет равна …
будет равна …
 |  | 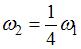 | |
 | 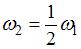 | ||
 | 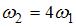 | ||
 | 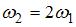 |
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Элементы специальной теории относительности
Космический корабль летит со скоростью 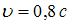 (
( 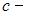 скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения другого космонавта …
скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения другого космонавта …
 |  | равна 1,0 м при любой его ориентации | |
 | изменяется от 1,0 м в положении 1 до 1,67 м в положении 2 | ||
 | изменяется от 1,0 м в положении 1 до 0,6 м в положении 2 | ||
 | изменяется от 0,6 м в положении 1 до 1,0 м в положении 2 |
