ЛЕКЦИЯ № 28. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Вопрос 1. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Фундаментальная система решений.
Рассмотрим линейное дифференциальное однородное дифференциальное уравнение с постоянными коэффициентами
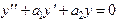 .
.
Будем искать решение этого уравнения в виде 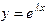 . Вычисляя производные
. Вычисляя производные
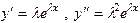
и подставляя их в уравнение, получим
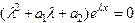
Так как 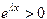 , то сокращая на , получим квадратное уравнение для определения
, то сокращая на , получим квадратное уравнение для определения
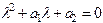 .
.
Это квадратное уравнение называется характеристическим уравнением. Рассмотрим следующие три случая:
1) характеристическое уравнение имеет разные вещественные корни, то есть его дискрименант строго положителен (D > 0).
Обозначим эти корни через 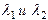 . Тогда получаем два решения
. Тогда получаем два решения
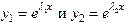
Эти решения образуют Ф.С.Р., так как их определитель Вронского отличен от нуля в точке x = 0
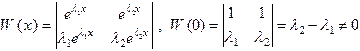
Следовательно, общее решение этого уравнения дается формулой
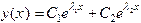 .
.
2) характеристическое уравнение имеет один вещественный корень , то есть его дискрименант D = 0.
В этом случае имеется одно решение 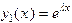 . Зная его, найдем второе решение
. Зная его, найдем второе решение 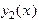 , используя формулу (смотри лекцию № 8)
, используя формулу (смотри лекцию № 8)
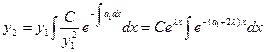
Так как D = 0, то 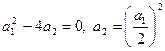 . Поэтому получаем
. Поэтому получаем
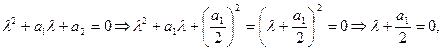
следовательно,
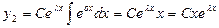 .
.
Итак фундаментальная система решений имеет вид
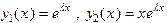
Общее решение уравнения есть
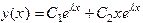
3) характеристическое уравнение имеет комплексные корни 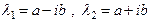 , то есть его дискрименант D < 0.
, то есть его дискрименант D < 0.
Тогда имеется два решения
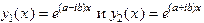 .
.
Эти решения являются комплексными функциями вещественного аргумента x. Удобно искать решения в виде вещественных функций. Для этого используем формулы Эйлера
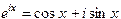 ,
,
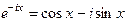 .
.
Тогда получим
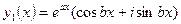 ,
,
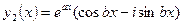 ,
,
Возьмем полусумму и полуразность этих решений
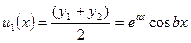
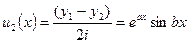
Тогда мы получим Ф.С.Р. , что легко подтвердить, вычисляя определитель Вронского
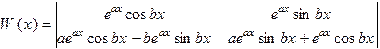 .
.
Вычисляя его при x = 0, получим
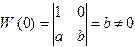
Следовательно, общее решение этого уравнения имеет вид
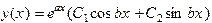
ПРИМЕР 1. Найти общее решение уравнения 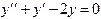 .
.
Составляем характеристическое уравнение 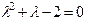 . Его корни равны
. Его корни равны 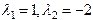 , тогда Ф.С.Р. есть
, тогда Ф.С.Р. есть
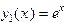 ,
, 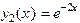 ,
,
отсюда находим общее решение уравнения 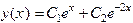 .
.
КОНЕЦ ПРИМЕРА.
ПРИМЕР 2. Найти общее решение уравнения 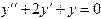 .
.
Составляем характеристическое уравнение 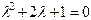 . Оно имеет один корень
. Оно имеет один корень 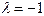 , тогда Ф.С.Р. есть
, тогда Ф.С.Р. есть
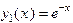 ,
, 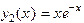 ,
,
отсюда находим общее решение уравнения 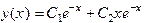 .
.
КОНЕЦ ПРИМЕРА.
ПРИМЕР 3. Найти общее решение уравнения 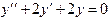 .
.
Составляем характеристическое уравнение 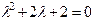 . Оно имеет комплексные корни
. Оно имеет комплексные корни 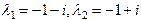 , тогда Ф.С.Р. есть
, тогда Ф.С.Р. есть
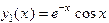 ,
, 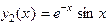 ,
,
отсюда находим общее решение уравнения 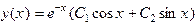 .
.
Конец примера.
