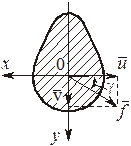
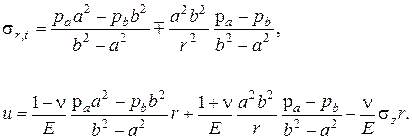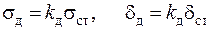Распределение нормальных напряжений

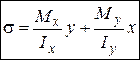или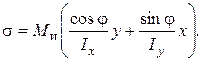

Условия прочности:

- для балок произвольного сечения из хрупких материалов

-

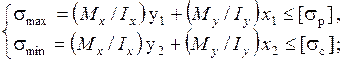для балок прямоугольного сечения из пластичных материалов

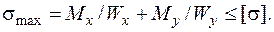
Полное перемещение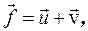

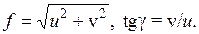
Условие жесткости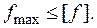

Примечание. При плоском косом изгибе .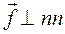

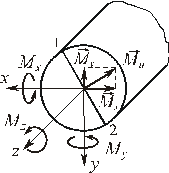10.2. Изгиб с кручением

10.2.1. Стержень круглого сечения

Условие прочности

,

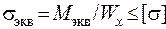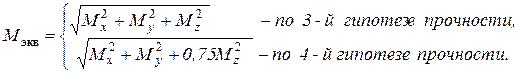
10.2.2. Стержень прямоугольного сечения

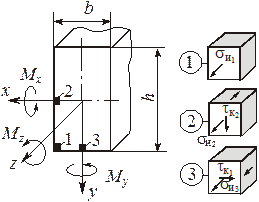
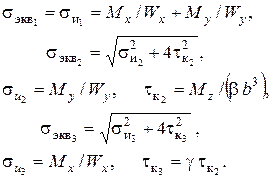
Условие прочности .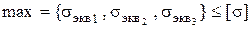

Внецентренное продольное нагружение

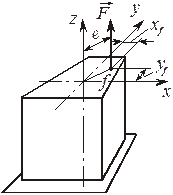Распределение нормальных напряжений

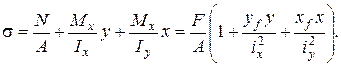
Знак «плюс» соответствует растяжению, «минус» – сжатию.

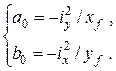Отрезки, отсекаемые нейтральной линией

на осях координат

В н е ц е н т р е н н о е с ж а т и е

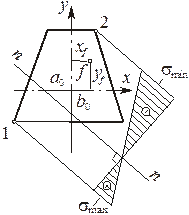Условия прочности

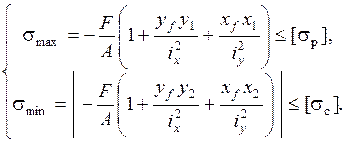
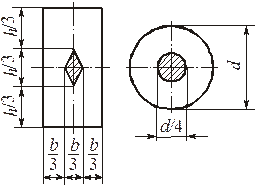
Ядро сечения

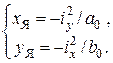
Координаты вершин

УСТОЙЧИВОСТЬ ДЕФОРМИРУЕМЫХ СИСТЕМ

Продольный изгиб

Формула Эйлера

(стержни большой гибкости, для которых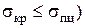

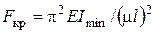или

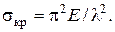
Формула Тетмайера-Ясинского

(стержни средней гибкости, для которых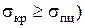

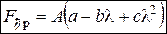или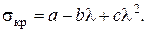

Гибкость стержня 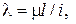где 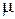– коэффициент приведения.

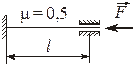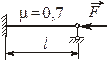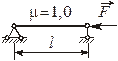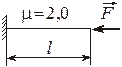Условие устойчивост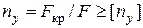и или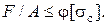

Внецентренное нагружение	Учет начального искривления
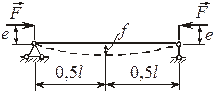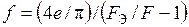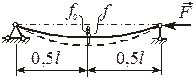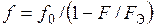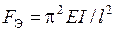– эйлерова критическая сила

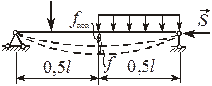11.2. Продольно-поперечный изгиб

Максимальный прогиб

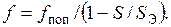
Максимальное напряжение

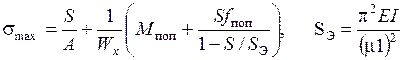эйлерова

– критическая

сила.

Условие прочности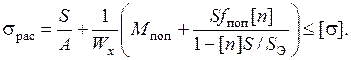

Условие жесткости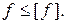

Устойчивость труб

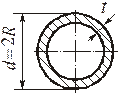Критическая нагрузка

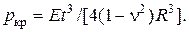
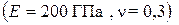Для стальных труб

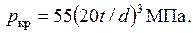
Условие устойчивости .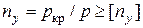

ДИНАМИЧЕСКОЕ НАГРУЖЕНИЕ

Общие зависимости

Учет сил инерции

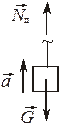Поступательное движение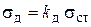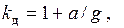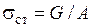

Равномерно вращающееся тонкое кольцо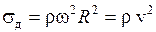

12.2. Действие удара на конструкцию

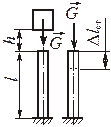
Продольный Удар в канатах Поперечный удар

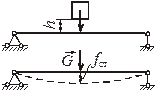удар при заедании троса

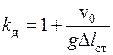
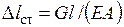
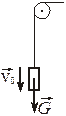
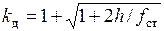
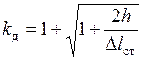
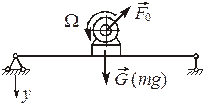12.3. Колебания упругих систем с одной степенью свободы

Уравнение колебаний упругой системы (неустановившееся движение)

,

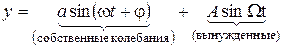происходящих под действием возмущающей силы 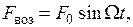где 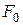– центробежная сила инерции неуравновешенных масс ротора. Частота собственных колебаний упругой системы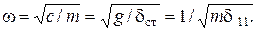

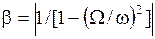
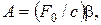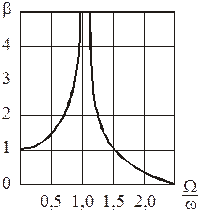
Амплитуда вынужденных колебаний

– коэффициент

нарастания колебаний.

Динамический коэффициент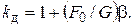

ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ

Характерные циклы: -симметричный

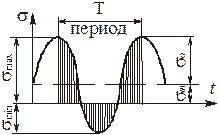
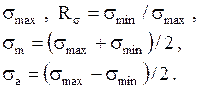Параметры цикла:

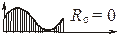
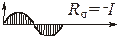
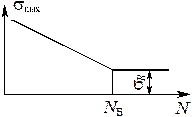Предел выносливости 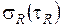- наибольшее напряжение цикла, которое образец может выдержать, не разрушаясь, до базы испытания 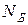, равной 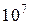циклов для стали и (5...10) 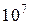для цветных металлов.

Эмпирические соотношения для :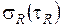

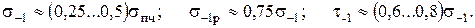
Факторы, влияющие на величину предела выносливости:

1) абсолютные размеры поперечного сечения (масштабный фактор)

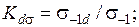
2) концентрация напряжений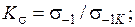

3) качество обработки поверхности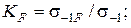

4) поверхностное упрочнение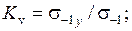

5) асимметрия цикла (коэффициенты чувствительности ;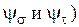

6) эксплуатационные факторы (коррозия, температура и др.).

Коэффициент снижения предела выносливости

.

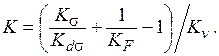
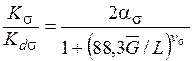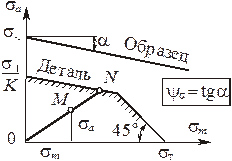Запас прочности определяется:

- по формуле Серенсена - Кинасошвили (при простых видах деформации)

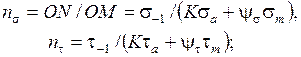
- по формуле Гафа и Полларда (при плоском напряженном состоянии) .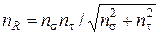

ТОНКОСТЕННЫЕ СОСУДЫ

Исходные допущения:

- сосуды имеют форму тела вращения без резких переходов и изломов с тонкой стенкой ;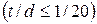

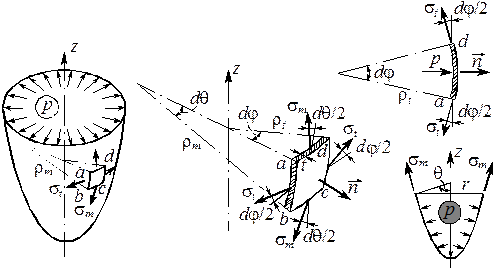- нагрузка является осесимметричной.

Разрешающие уравнения для определения ме­ридионального 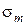и окружного 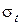напряжений:

- уравнение Лапласа (получается из уравнения равновесия элемента abcd в проекции на нормаль )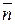

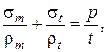- уравнение равновесия части сосуда, отсеченной нормальным коническим сечением, в проекции на ось сосуда z

.

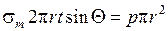Сферический сосуд	Цилиндрический сосуд

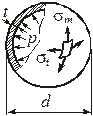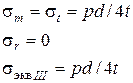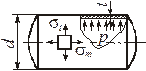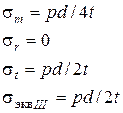Условие прочности .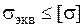

ТОЛСТОСТЕННЫЕ ТРУБЫ

Допущение: нагрузка осесимметрична и постоянна вдоль оси.

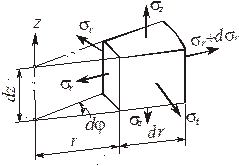Основные уравнения:

- уравнение равновесия

,

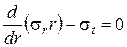- геометрические

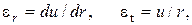
- физические (закон Гука)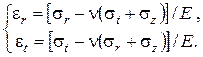

Разрешающие уравнения 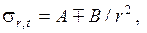где А и В – произвольные постоянные, определяемые из граничных условий задачи.

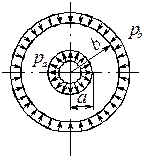15.1. Труба, нагруженная внутренним и внешним давлением(задача Ламе)