Динамический синтез насоса.

Динамический синтез насоса проводим с целью повышения его общего к.п.д. путём снижения теплового излучения обмоток приводного электродвигателя при неравномерном вращении ротора внутри цикла.

Задачу решают подбором и перераспределением масс звеньев, введением, при необходимости, дополнительной массы с постоянным моментом инерции в виде маховика. Предварительно анализируем инертные свойства имеющихся механизмов.

Расчёт масс и моментов инерции звеньев.

Инертные свойства звеньев характеризуют показатели массы (при поступательном движении) и момента инерции (при вращательном).

В первом приближении можно принять, что по длине рычагов массы распределены равномерно, что интенсивность распределения q = 30 кг/м и что зубчатые колёса – сплошные диски.

Массы рычагов определяются как: m_i = q×l_i

Моменты инерции звеньев относительно их центров масс находим как ,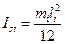

а относительно оси вращения (для вращательных звеньев): .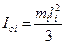

Массы зубчатых колёс определяются через делительные диаметры и межосевые расстояния a_w по формуле: .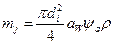

Моменты инерции колёс относительно оси вращения определим через их массу и делительный диаметр как для однородных дисков: .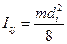

Массу водила планетарной ступени редуктора находим с помощью формулы:

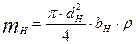
где ширину водила принимаем равной толщине смонтированного в нём саттелита Z₂, т.е. b_H=a_w×ψ_a ; ψ_a =0.25 ; b_H = 0.0394м

C учётом этого: 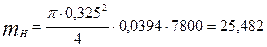кг

Момент инерции определяем как для сплошного диска: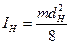

I_H = 25,482×0,325²/8 = 0,3364 кг×м²

Массу кулачка m_k и момент инерции I_к оцениваем по среднему его радиусу:

R_ср = (2R₀+H)/2

R_ср = (2·0.0273731+0.15)/2 = 0.1024 м ;

и ширине b_k , которую мы задаём как

b_k = 0,2×D_{ср ;} b_k = 0,2·2·0,1024 = 0,04096мм

В этом случае:

;

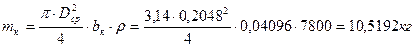а момент инерции

I_k = m_k×D²_ср/8

I_k = 10,5192·×0,0,2048²/8 = 0,0552 кг×м

Момент инерции ротора электродвигателя определяем по маховому моменту

m_pD² _p = 0,58 кг×м². Получаем:

I_p = m_pD² _p/8

I_p = 0,58/8 =0,0725 кг×м².

Динамические характеристики остальных движущихся звеньев из-за малых их масс, либо скоростей точек, считаем пренебрежимо малыми и далее не учитываем.

Полученные результаты расчётов заносим в таблицу 6.1. таблица 6.1

Наименование звена	Обозначение звена	Наименование параметра и его обозначение
Длина рычага, диаметр колеса, м	Масса, кг	Момент инерции относительно оси вращения, кг×м2.	Момент инерции относительно центра масс, кг×м2.
Рычаг	AB ВC CDF	0,071 0,393 0,440	2,13 11, 79 13,2	0,0036 ____ 0,8518	____ 0,1517 ____
Зубчатые колёса	Z1 Z2 Z4 Z5	0,090 0,225 0,114 0,204	1,9529 12,2053 3,1631 10,1289	0,00198 0,0772 0,00514 0.05269
Ползун	F	___	39,6	___	___
Водило	H	0.325	25,482	0,3364
Кулачок	___	___	10,5192	0,0552	0,0552
Ротор электродвигателя	___	___	___	0,0725	0,0725

Расчёт приведённых моментов инерции.

Инертные свойства машин и механизмов характеризуют приведённой массой, либо приведённым моментом инерции, в зависимости от того, линейным или угловым является перемещение звена приведения.

Приведённый момент инерции механизма может быть приведён к главному валу машины, для чего его величину умножают на квадрат передаточной функции от звена приведения к указанному валу.

Приведённый к главному валу машины момент инерции её маховых масс вычисляют как сумму произведений масс и моментов инерции её звеньев, а также приведённых масс; либо приведённых моментов инерции её механизмов, на квадраты передаточных функций в движении приводимых звеньев и звеньев приведения относительно вала машины, принятого

за главный.

Главным приведённым моментом насоса будет момент, приведённый к валу кривошипа АВ.

Приведённый момент ротора приведённого электродвигателя:

I_p.пр = I_p×U_пер² = 0,0725×12,72² = 11,73 кг×м²

Приведённый момент зубчатой передачи:

I_{пер. пр.} = (I_пл + I_Z4)×U_4-5 + I_Z5 ,

где I_пл – приведенный к валу водило момент инерции планетарного механизма, а величину I_пл вычисляем:

I_пл = I_н + I_Z1× U_пл² + k×(m_Z2(V₀₁/ω_H)²+ I_Z2×(ω₂/ω_H)²); где k – число сателлитов

Передаточная функция :

V₀₁/ω_H = l_H = (d₁+d₂)/2 = (0,090+0,225)/2 = 0,1575м

ω₂/ω_H = (Z₁+Z₂)/Z₂ = (d₁+d₂)/d₂

ω₂/ω_H = (0,090+0,225)/0,225 = 1,4, а U_пл= 7

Остальные данные берем из таблицы 6.1.

Получаем:

I_пл = 0,3364+ 0,00198×49+3(12,2053×0,1575²+0,0772·1,4²)= 1,7957 кг×м²

При этом:

I_{пер. пр} = (1,7957+0,00514) ·1,81²+0,05269 = 5,9520 кг×м²

Приведенный момент инерции кулачкового механизма:

I_поп.пр. = I_к=0,0552 кг×м²

Приведенный момент инерции несущего механизма:

I_нес.пр. = I₀₁+m₂(V_s2/ω₁)²+I_s2(ω₂/ω₁)²+ I₀₃(ω₃/ω₁)²+ m₅(V₅/ω₁)²;

где передаточная функция в движении ползуна 5 относительно кривошипа АВ может быть

вычислена как:

V₅/ω₁ = ω₃/ω_{1 *} V₅/ω₃; где V₅/ω₃ = V_В/ω₁ = Н/cos²φ₁^*

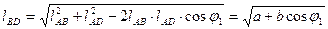
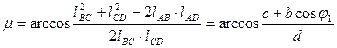, где

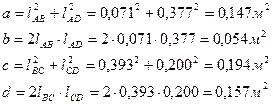
Далее получаем:

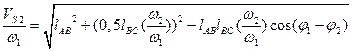
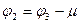
Значения координаты φ⁰₁ – угла кривошипа АВ с направлением стойки AD – замеряем

непосредственно из плана положений.

Полученные результаты расчетов заносим в таблицу 6.2 и 6.3:

таблица 6.2

N положения механизма	φ01	μ0	φ02	φ03	ω2/ω1	ω3/ω1	Vs2/ω1	V5/ω1
		26,91	133,92	160,83	-0,3990	0,7104	0,0826	0,1482
		25,77	123,42	149,19	-0,2877	0,7652	0,1051	0,1596
		18,70	131,06	149,76	0,0271	0,3041	0,0659	0,0634
		35,11	95,08	130,19	0,1084	0,1589	0,0507	0,0331
		22,50	129,18	151,68	0,4654	-0,9045	0,1158	-0,1887
		26,37	129,25	155,62	0,2238	-0,6904	0,1006	-0,1440
		26,90	39,73	66,63	0,3666	-0,5015	0,0486	-0,1046
		26,24	132,49	158,73	0,0799	-0,4889	0,0840	-0,1020
		16,06	155,12	171,18	-0,3084	0,2694	0,0173	0,0562

Положения кривошипа АВ	Значение обоб. координаты φ010	Приращение кинетической энергии ∆Т, Дж	Момент инерции, приведенный к валу кривошипа ОА, кг×м2
Iр.пр	Iпер.пр	Iнес.пр
			11,73	5,9520	1,4402
		-164,3	11,73	5,9520	1,6861
		-345,03	11,73	5,9520	0,3253
		-476,47	11,73	5,9520	0,1330
		-657,2	11,73	5,9520	2,3340
		-361,46	11,73	5,9520	1,3901
		-312,17	11,73	5,9520	0,7317
		-295,74	11,73	5,9520	0,7357
		-268,88	11,73	5,9520	0,2409
			11,73	5,9520	1,4402

таблица 6.3

φ⁰₁₀ – угол поворота кривошипа АВ от своего нулевого положения, соответствующего одному из крайних положений ползуна.

В таблице определено:

∆Т_i=А_дi-Ас_i

На листе 1 строим диаграмму энергомасс – зависимость ∆Т_i от ∆I_прi. С помощью этой диаграммы находим момент инерции постоянной составляющей маховых масс(I^*_пр), при которой частота вращения приводного электродвигателя за цикл установившегося движения изменяется

соответственно допустимому коэффициенту δ изменения средней скорости хода. Такое ограничение необходимо для предохранения приводного электродвигателя от перегрева, для повышения общего к.п.д. работы насоса за счет снижения получаемого тепла обмотками электродвигателя. Принимаем:

δ=0,04

Средняя угловая скорость вала кривошипа АВ:

ω_ср= π·n_кр/30 = π·231,48/30 = 24,2 с^-1

Углы наклона касательных к диаграмме энергомасс определяем по формулам:

tgψ_max=μ_I·(1+ δ)·ω_ср²/(2· μ_T);

tgψ_min=μ_I·(1-δ)· ω_ср²/(2· μ_T); где

μ_I=0,03 кг×м²/мм;

μ_T=30 Дж/мм – масштабы приведенного момента инерции и энергии, выбранные для диаграммы энергомасс.

После подстановки чисел получаем:

tgψ_max=0,03·(1+0,04)·24,2²/(2·30)=0,30453;

tgψ_min=0,03·(1-0,04)·24,2²/(2·30)=0,28111;

Откуда:

ψ_max=16,94⁰; ψ_min=15,7⁰

Проведя касательные к диаграмме под указанными углами к оси ∆I_прi, находим отрезки О₁К и О₁L(в мм), которые используем для определения координат начала О системы Т- I_пр - зависимости полной кинетической энергии движущихся звеньев механизма от их приведенного момента инерции (О₁К = 1,5мм; О₁L=-93мм).

Уравнения касательных:

y=x tgψ_max+ О₁К;

y=x tgψ_min+ О₁L;

Решаем совместно вычитанием второго уравнения из первого:

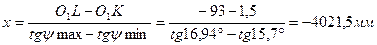
После чего подстановка в первое уравнение дает:

y=-4021,5·tg16,94+1,5=-1223,39 мм

Постоянная составляющая момента инерции насоса:

I_пр^*=x×μ_I=4021,5·0.03=120,645 кг×м²

T₀=y× μ_T=1223,39·30=36701,7 Дж

Чтобы перейти от системы координат ∆Т-∆I к системе Т-I_пр, вычислим:

Т=Т₀+∆Т_max= 36701,7-657,2=36044,5 =36,0445 кВт·сек=36,0445/3600=1,001·10^-2 кВт·ч

Что соответствует подводимой из сети энергии

Т^*=Т/η_дв=1,001·10^-2 /0,98=1,021·10^-2 кВт·ч.

Максимальный маховый момент определим по следующей формуле

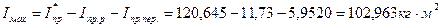
Задаваясь радиусом маховика r=0,5 м примем его массу m_мах=102.963/0,5²=411,852 кг.

Переносим маховик на более быстроходный вал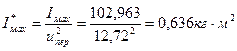

Пересчитываем массу маховика m_мах=0,636/0,5²=2,544 кг

Определяем ориентировочную массу звеньев станка.

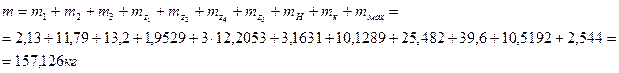
а с учетом массы электродвигателя, соединительных валов и деталей (принимаем м_соед=0,1·м), станины (принимаем м_стан=1,2·м), ориентировочная масса станка оказывается приблизительно равной

М=м+0,1·м+1,2·м=2,3·м=361,4 кг.