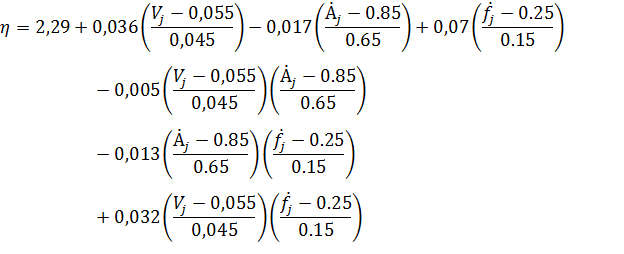Построение квазилинейной регрессионной модели
Р.В. Дюгуров
планирование эксперимента. Построение линейных, нелинейных и квазилинейных уравнений регрессии
Пояснительная записка
к курсовому проекту
По дисциплине: Основы научных исследований, организация и планирование эксперимента.
Направление подготовки магистров: 15.04.01 «Машиностроение»
Профиль ООП: «Процессы и машины обработки металлов давлением»
Группа 53304/11
Руководитель проекта: Востров В.Н
д.т.н
| Допущена к защите: ‹‹___››_________2016г. | Заведующий кафедрой Радкевич М.М. |
САНКТ – ПЕТЕРБУРГ, 2016 г.
Содержание
1.Задание 1: основы теории подобия и размерности…………………………3
2.Задание 2 : планирование эксперимента. Построение линейных и квазилинейных уравнений регрессии………………………………………….6
3. Задание 3: планирование эксперимента. Построение нелинейных уравнений регрессии……………………………………………………………15
Список литературы……………………………………………………………..24
Задание №1. Основы теории подобия и размерностей
Вариант 7
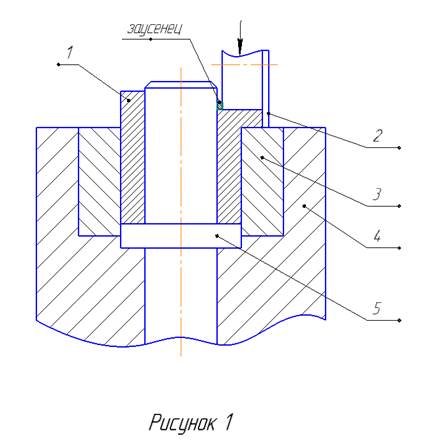
Торцевая раскатка цилиндрическим валком применяется при деформировании торцевой части трубчатых заготовок и формировании на них фланца. Заготовка 1 устанавливается на оправку 5 и размещается в матрице 3, которая фиксируется в обойме 4 (рис. 1). Обойма 4 приводится во вращение. Заготовка 1 деформируется валком 2, который вращается за счет сил трения между заготовкой 1 и обоймой 4. При поступательном перемещении валка 2 осуществляется процесс высадки наружного бурта. Установить в критериальной форме функциональную связь усилия деформирования P с факторами.
Решение
Функциональная зависимость, подлежащая исследованию:
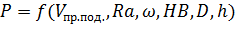
Выберем три величины: 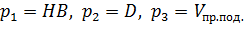 . Докажем, что применительно к системе измерений основных величин MLT эти величины являются независимыми. Уравнения размерностей для данных величин:
. Докажем, что применительно к системе измерений основных величин MLT эти величины являются независимыми. Уравнения размерностей для данных величин:
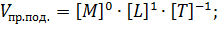
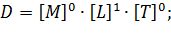
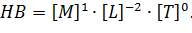
Вычислим определитель, составленный из показателей степеней в уравнениях размерностей:
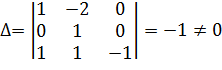
Следовательно 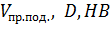 – независимые величины..
– независимые величины..
Запишем уравнения размерностей для остальных параметров:
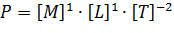
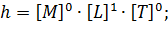
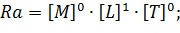
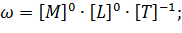
Представим безразмерные 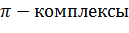 в виде отношений произвольной величины к независимым величинам:
в виде отношений произвольной величины к независимым величинам:
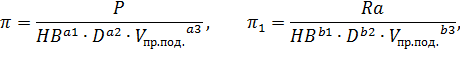
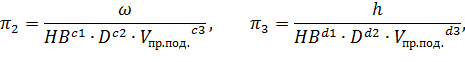
Обобщенная характеристика 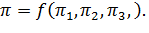 Подставим в формулы
Подставим в формулы 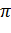 размерности величин параметров.
размерности величин параметров.
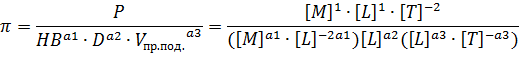
Сравниваем показатели одноименных основных величин:
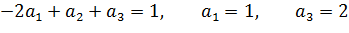
Отсюда 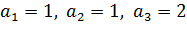 . Безразмерный комплекс
. Безразмерный комплекс 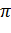 имеет вид:
имеет вид:
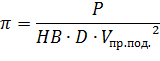
Аналогично выразим остальные 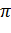 -комплексы:
-комплексы:
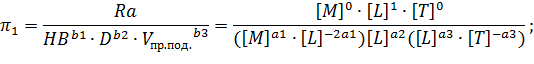
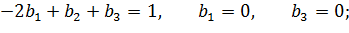
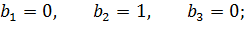
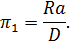
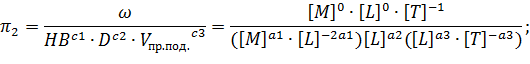
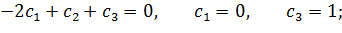
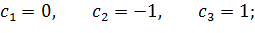
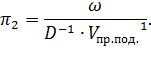
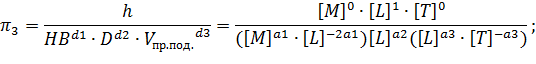
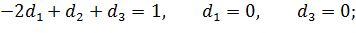
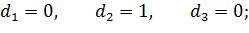
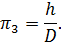
Получили:
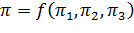
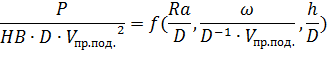
Задание №2. Планирование эксперимента. Построение линейных и квазилинейных уравнений регрессии
Вариант 16
Величина микронеровностей 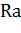 при токарной обработке зависит от относительной скорости резания
при токарной обработке зависит от относительной скорости резания 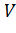 , амплитуды колебаний
, амплитуды колебаний 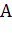 и частоты колебаний
и частоты колебаний 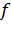 заготовки, представлены в таблице 1.
заготовки, представлены в таблице 1.
Таблица 1 – Зависимость интенсивности напряжений
| Номер | 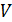 | 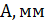 | 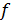 , , 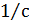 | 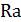 , мкм , мкм | ||
| 0,1 | 1,5 | 0,4 | 2,41 | 2,25 | ||
| 0,1 | 0,2 | 0,4 | 2,39 | 2,4 | ||
| 0,1 | 1,5 | 0,1 | 2,29 | 2,28 | ||
| 0,1 | 0,2 | 0,1 | 2,29 | 2,25 | ||
| 0,1 | 0,2 | 0,4 | 2,42 | 2,45 | ||
| 0,055 | 1,5 | 0,4 | 2,35 | 2,38 | ||
| 0,055 | 0,2 | 0,2 | 2,32 | 2,3 | ||
| 0,01 | 1,5 | 0,1 | 2,26 | 2,25 | ||
| 0,01 | 1,5 | 0,4 | 2,25 | 2,23 | ||
| 0,01 | 1,5 | 0,2 | 2,2 | 1,15 | ||
| 0,01 | 0,2 | 0,1 | 2,27 | 2,24 | ||
| 0,01 | 0,2 | 0,4 | 2,29 | 2,28 | ||
1. Выбрать из таблицы данные для составления плана эксперимента;
2. Построить квазилинейную регрессионную модель;
3. Выполнить критериальные проверки.
Решение
Составление плана эксперимента
В нашем опыте независимыми переменными являются скорости резания 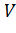 , амплитуды колебаний
, амплитуды колебаний 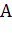 и частоты колебаний
и частоты колебаний 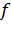 заготовки, зависимой переменной является величина микронеровностей
заготовки, зависимой переменной является величина микронеровностей 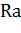 .
.
Для математической обработки данных эксперимента необходимо перейти от реальных физических величин к нормированным, т.е. расположенным в интервале 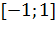 .
.
Интервалы изменения площади вырезаемого грунта, ширины ковша и прочности грунта:
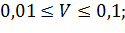
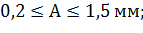
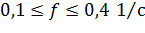 .
.
Вычислим основной уровень для изменения скорости резания 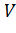 , амплитуды колебаний
, амплитуды колебаний 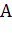 и частоты колебаний
и частоты колебаний 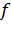 заготовки:
заготовки:
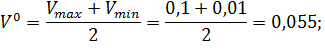
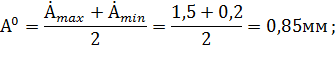
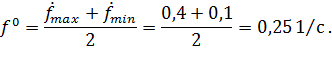
Вычислим интервал варьирования для изменения температуры 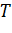 и скорости деформации
и скорости деформации 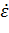 :
:
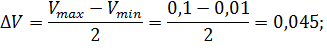
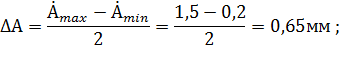
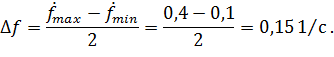
Нормированные значения факторов обозначим через 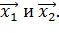
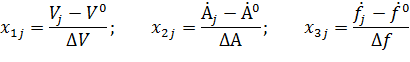
В результате получим план эксперимента:
Таблица 2 – План эксперимента
| № опыта | Факторы | Значения отклика в повторных опытах | Выборочное среднее отклика | |||
| i | 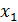 | 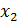 | 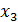 | 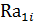 | 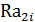 | 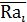 |
| 2,41 | 2,25 | 2,3 | ||||
| -1 | 0,333333 | 2,39 | 2,4 | 2,4 | ||
| -1 | 2,29 | 2,28 | 2,3 | |||
| -1 | -1 | 2,29 | 2,25 | 2,3 | ||
| -1 | 2,42 | 2,45 | 2,4 | |||
| 2,35 | 2,38 | 2,4 | ||||
| -1 | -0,33333 | 2,32 | 2,3 | 2,3 | ||
| -1 | -1 | 2,26 | 2,25 | 2,3 | ||
| -1 | 2,25 | 2,23 | 2,2 | |||
| -1 | -0,33333 | 2,2 | 1,15 | 1,7 | ||
| -1 | -1 | 2,27 | 2,24 | 2,3 | ||
| -1 | -1 | -1 | 2,29 | 2,28 | 2,3 |
Количество опытов в плане полного факторного эксперимента определяется по формуле:
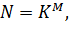 (1.1)
(1.1)
Где K – количество уровней, M – количество факторов.
План эксперимента из таблицы 2 не соответствует соотношению (1.1), так как 12≠63, следовательно необходимо исключить из плана два уровня факторов, чтобы соотношение (1.1.) приняло вид 8=23.
Оставим в плане только максимальные и минимальные уровни факторов, с целью увеличить интервал варьирования и избежать в дальнейшем получения незначимых коэффициентов квазилинейной модели.
Тогда план полного факторного эксперимента примет следующий вид:
Таблица 3 – План полного факторного эксперимента
| № опыта | Факторы | Значения отклика в повторных опытах | Выборочное среднее отклика | |||
| i | 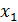 | 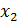 | 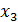 | 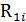 | 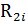 | 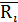 |
| 2,41 | 2,25 | 2,33 | ||||
| -1 | 2,29 | 2,28 | 2,285 | |||
| -1 | -1 | 2,29 | 2,25 | 2,27 | ||
| -1 | 2,42 | 2,45 | 2,435 | |||
| -1 | -1 | 2,26 | 2,25 | 2,24 | ||
| -1 | 2,25 | 2,23 | 2,24 | |||
| -1 | -1 | 2,27 | 2,24 | 2,255 | ||
| -1 | -1 | -1 | 2,29 | 2,28 | 2,285 |
Данный план является полным, т.к. обладает следующими свойствами:
· Алгебраическая сумма элементов вектора-столбца каждого фактора равна нулю. Данное свойство называется симметричностью плана:
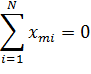
· Сумма почленных произведений любых двух векторов-столбцов равна нулю: 
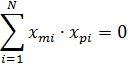
· Сумма квадратов элементов столбца каждого фактора равна количеству опытов N:
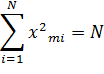
Построение квазилинейной регрессионной модели
Построим квазилинейную статистическую (регрессионную) модель вида:
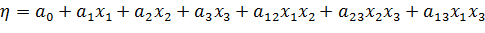
Для нахождения коэффициентов am модели воспользуемся свойствами вектор-столбцов полного факторного эксперимента. Это позволит вычислить их по формулам:
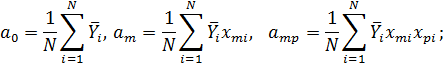
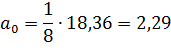
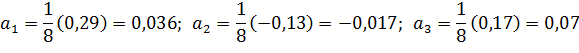
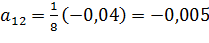 ;
; 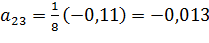 ;
; 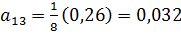
Получили модель:
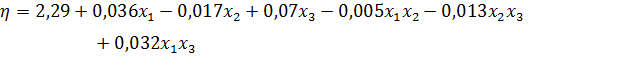
Перейдём от нормированных значений факторов к их натуральным значениям: