ЗАНЯТИЕ 4. Уравнения в полных дифференциалах.
| Ауд. | Л-3 | гл.10: № 96, 98, 100, 102, 104, 149, 154,171,187. |
☺ ☻ ☺
Пример 1–96: Решить дифференциальное уравнение: (2x+y)dx+(x+2y)dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). Проверим выполнение условия:  =
=  . Если условие выполняется, то заданное уравнение в полных дифференциалах.
. Если условие выполняется, то заданное уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 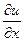 : u(x,y)=
: u(x,y)=  + φ(y), (1)
+ φ(y), (1)
где φ(y) отражает ту часть функции u(x,y), которая была «уничтожена» при дифференцируемости по переменной х.
a1. Подберем φ(y) так, чтобы выполнялось условие: 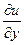 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 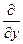
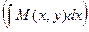 + φ′(y)= N(x,y). (2)
+ φ′(y)= N(x,y). (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)– 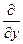
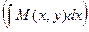 . (3)
. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  . (4)
. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  +С. (5)
+С. (5)
3). В нашем случае:  =1 и
=1 и  =1 → условие
=1 → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
a0. Находим первообразную функции М = 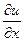 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 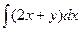 + φ(y)=x2+xy+φ(y). (1)
+ φ(y)=x2+xy+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 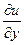 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 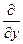 ( x2+xy)+φ′(y)= x+φ′(y)=N(x,y); (2)
( x2+xy)+φ′(y)= x+φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–x=(x+2y) –x=2y. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =y2. (4)
=y2. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  = x2+xy+ y2= С. (5)
= x2+xy+ y2= С. (5)
Ответ: u(x,y)= x2+xy+ y2= С – общее решение.
Пример 2–98: Решить дифференциальное уравнение: (3x2+6xy–2y2)dx+(3x2–4xy–3y2)dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =6x–4y и
=6x–4y и  =6x–4y → условие
=6x–4y → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 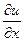 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 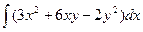 +φ(y)=x3+3x2y–2xy2+φ(y). (1)
+φ(y)=x3+3x2y–2xy2+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 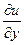 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 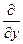 (x3+3x2y–2xy2)+φ′(y)=3x2–4xy +φ′(y)=N(x,y); (2)
(x3+3x2y–2xy2)+φ′(y)=3x2–4xy +φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–x=(3x2–4xy–3y2)–( 3x2–4xy)=–3y2. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =–y3. (4)
=–y3. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =x3+3x2y–2xy2–y3= С. (5)
=x3+3x2y–2xy2–y3= С. (5)
Ответ: u(x,y)=x3+3x2y–2xy2–y3= С – общее решение.
Замечание: 1). Пример интересен тем, что заданное ДУ можно отнести и к однородным уравнениям: функции М(x,y) и N(x,y) – обе однородные, порядка 2. Если «попробовать» решать его по схеме однородного уравнения, то трудоёмкость «процесса» возрастет в разы: f(u)–u= 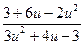 –u=
–u= 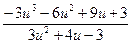 → J=
→ J= 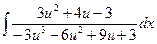 .
.
2). Ещё бо′льшим будет «интерес», если обратить внимание на «ситуацию» возможного равенства: f(u)–u=0. По основной теореме алгебры мы получим (!) три корня: u=u1, u=u2, u=u3 → получаем дополнительно три решения ДУ:
y= u1x; y= u1x; y= u1x – прямые, проходящие через начало координат.
3). Рассмотренная ситуация подсказывает будущему инженеру: в ответственных случаях желательно получить решение несколькими возможными способами!
Пример 3–100: Решить дифференциальное уравнение: 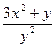 dx–
dx– 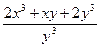 dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  = –
= – 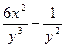 и
и  = –
= – 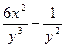 → условие
→ условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 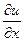 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 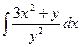 +φ(y)=
+φ(y)= 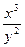 +
+ 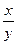 +φ(y). (1)
+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 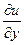 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 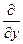
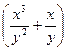 +φ′(y)= –2
+φ′(y)= –2 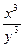 –
– 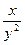 +φ′(y)=N(x,y); (2)
+φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)+2 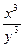 +
+ 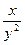 =2. (3)
=2. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =2y. (4)
=2y. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =
= 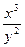 +
+ 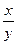 +2y= С. (5)
+2y= С. (5)
Ответ: u(x,y)= 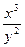 +
+ 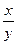 +2y= С – общее решение.
+2y= С – общее решение.
Пример 4–102: Решить дифференциальное уравнение: (2x–y∙e–x)dx+e–xdy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  = –e–x и
= –e–x и  = –e–x → условие
= –e–x → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 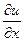 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 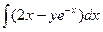 +φ(y)= x2+y∙e–x +φ(y). (1)
+φ(y)= x2+y∙e–x +φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 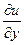 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 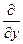 (x2+y∙e–x)+φ′(y)= e–x+φ′(y)=N(x,y); (2)
(x2+y∙e–x)+φ′(y)= e–x+φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–e–x =0. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =C. (4)
=C. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =x2+y∙e–x=С. (5)
=x2+y∙e–x=С. (5)
Ответ: u(x,y)=x2+y∙e–x=С – общее решение.
Пример 5–104: Решить дифференциальное уравнение: 2x∙cos2ydx+(2y–x2sin2y)dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =–2x∙sin2y и
=–2x∙sin2y и  =–2x∙sin2y → условие
=–2x∙sin2y → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 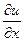 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 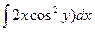 +φ(y)=x2cos2y+φ(y). (1)
+φ(y)=x2cos2y+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 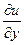 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 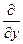 ( x2cos2y)+φ′(y)=–x2sin2y+φ′(y)=N(x,y); (2)
( x2cos2y)+φ′(y)=–x2sin2y+φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–x2sin2y=2y. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =y2. (4)
=y2. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =x2cos2y+y2=С. (5)
=x2cos2y+y2=С. (5)
Ответ: u(x,y)=x2cos2y+y2=С – общее решение.
Пример 6–149: Решить дифференциальное уравнение: (2x3–xy2)dx+(2y3–x2y)dy =0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =–2xy и
=–2xy и  =–2xy → условие
=–2xy → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 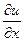 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 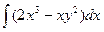 +φ(y)=
+φ(y)= 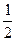 x4–
x4– 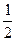 x2y2+φ(y). (1)
x2y2+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 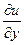 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 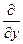
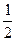 (x4– x2y2)+φ′(y)= x2y +φ′(y)=N(x,y); (2)
(x4– x2y2)+φ′(y)= x2y +φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–x2y=2y3. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =
= 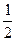 y4. (4)
y4. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =x4–x2y22xy2+y4= С. (5)
=x4–x2y22xy2+y4= С. (5)
Замечание: Для упрощения записи общего решения умножили на 2 (!) .
Ответ: u(x,y)=x4–x2y22xy2+y4= С – общее решение.
Пример 7–154: Решить дифференциальное уравнение: (2x+lny)dx+ 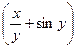 dy =0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
dy =0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =
= 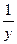 и
и  =
= 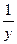 → условие
→ условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 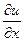 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 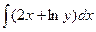 +φ(y)= x2+x∙lny+φ(y). (1)
+φ(y)= x2+x∙lny+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 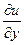 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 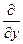 ( x2+x∙lny)+φ′(y)=
( x2+x∙lny)+φ′(y)= 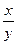 +φ′(y)=N(x,y); (2)
+φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)– 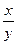 =siny. (3)
=siny. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  = –cosy. (4)
= –cosy. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =x2+x∙lny–cosy= С. (5)
=x2+x∙lny–cosy= С. (5)
Ответ: u(x,y)=x2+x∙lny–cosy= С – общее решение.
Пример 8–171: Найти уравнение кривой, проходящей через точку 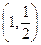 , если для любого отрезка [1,x] площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, на 2 больше отношения абсциссы x концевой точки к ординате y.
, если для любого отрезка [1,x] площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, на 2 больше отношения абсциссы x концевой точки к ординате y.
Решение:
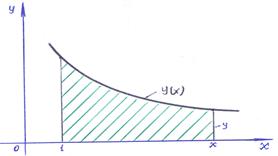 Замечание: а). При решении задачи используется производная интеграла по верхнему «переменному пределу»;
Замечание: а). При решении задачи используется производная интеграла по верхнему «переменному пределу»;
б). Необходимо отметить «безразличие» решения к «числу 2».
1) Составим «интегральное» уравнение:
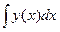 =
= 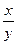 +2. (1)
+2. (1)
2). Дифференцируя (1), получаем дифференциальное уравнение:
y= 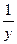 – x
– x 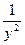 y′, или y′–
y′, или y′– 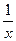 y=–
y=– 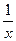 y3. (2)
y3. (2)
3). Уравнение (2) – уравнение Бернулли для n=3. Алгоритм решения стандартный:
a0. Примем: z = y–n+1, где (–n+1)= –2; то есть: z=y–2.
a1. Запишем преобразованное уравнение Бернулли: z′+2 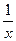 z=2
z=2 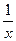 . (3)
. (3)
a2. Решение уравнения ищем в виде: функцию z=u(x)∙v(x);
a3. Вычислим интеграл: – 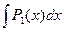 =–2
=–2 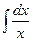 =–lnx2 → u=
=–lnx2 → u= 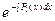 =
= 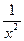 .
.
a4. Вычислим функцию v: v = 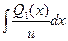 = 2
= 2 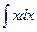 +С= x2 +С;
+С= x2 +С;
a5. Запишем общее решение уравнения для (3): z=u∙v= 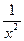 ∙( x2 +С). (4)
∙( x2 +С). (4)
a6. Учитывая: z=y–2, запишем общее решение для (1): y–2= 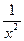 ∙( x2 +С), или (удобнее для использования): y2=
∙( x2 +С), или (удобнее для использования): y2= 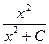 .
.
a7. Учитывая начальные условия, запишем частное решение: 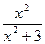 .
.
Ответ: y2= 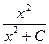 – общее решение уравнения. Частное решение:
– общее решение уравнения. Частное решение: 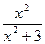 .
.
Замечание: решение y=0 в нашем случае «геометрически неинтересное», потому в ответе не отмечено.
Пример 8–187: Скорость охлаждения тела пропорциональна разности температур тела и окружающей среды (закон Ньютона). Найти зависимость температуры Т от времени t, если тело, нагретое до Т0 градусов, внесено в помещение, температура которого постоянна и равна а градусам.
 Решение:
Решение:
Замечание: рисунок «мотивирует» решение задачи, а также «намекает», что охлаждение тела происходит за счет «молекулярного взаимодействия» тела и среды: подвеска тела к потолку на тонкой нити с минимальной теплопроводностью.
1). Из условия задачи следует дифференциальное уравнение:
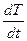 =–k(T–a). (1)
=–k(T–a). (1)
2). Уравнение (1) – ДУ с разделяющимися переменными. Его стандартная форма записи:
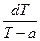 =–kdt. (2)
=–kdt. (2)
3). В результате интегрирования уравнения (2) получаем общее решение задачи:
T=a+Ce–kt. (3)
4). Учитывая начальные условия, получаем частное решение задачи:
T=a+(Т0–a)e–kt. (4)
Ответ: T=a+Ce–kt – общее решение уравнения. Частное решение: T=a+(Т0–a)e–kt.
* * * * * * * * * *
Домашнее задание
| Дома | Л-3 | гл.10: № 97, 99,101,103,105,143,181,188. |
Пример 1–97: Решить дифференциальное уравнение: (10xy–8y+1)dx+(5x2–8x+3)dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =10x–8и
=10x–8и  =10x–8 → условие
=10x–8 → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 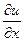 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 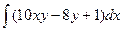 +φ(y)=5x2y –8xy+x+φ(y). (1)
+φ(y)=5x2y –8xy+x+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 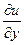 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 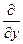 (5 x2y –8xy+x)+φ′(y)=5x2–8x +φ′(y)=N(x,y); (2)
(5 x2y –8xy+x)+φ′(y)=5x2–8x +φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–5x2+8x =3. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  =3y. (4)
=3y. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =5x2y–8xy+x+3y= С. (5)
=5x2y–8xy+x+3y= С. (5)
Ответ: u(x,y)= 5x2y–8xy+x+3y = С – общее решение.
Пример 2–99: Решить дифференциальное уравнение: 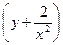 dx+
dx+ 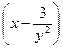 dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =1и
=1и  =1 → условие
=1 → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 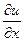 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 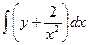 +φ(y)= xy–2
+φ(y)= xy–2 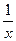 +φ(y). (1)
+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 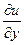 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 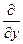
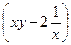 +φ′(y)= x +φ′(y)=N(x,y); (2)
+φ′(y)= x +φ′(y)=N(x,y); (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)= N(x,y)–x= 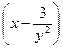 –x=–
–x=– 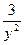 . (3)
. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  +С=3
+С=3 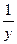 . (4)
. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  = xy–2
= xy–2 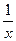 +3
+3 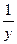 = С. (5)
= С. (5)
Ответ: u(x,y)=x3+3x2y–2xy2–y3= С – общее решение.
Пример 3–101: Решить ДУ: 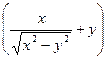 dx+
dx+ 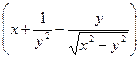 dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =1+xy
=1+xy 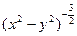 и
и  =1+xy
=1+xy 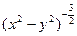 → условие
→ условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 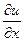 :
:
u(x,y)=  + φ(y)=
+ φ(y)= 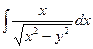 +
+ 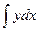 +φ(y)=
+φ(y)= 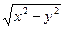 +xy+φ(y). (1)
+xy+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 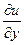 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 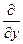 (
( 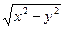 +xy)+φ′(y)= x–
+xy)+φ′(y)= x– 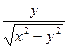 +φ′(y)=N(x,y). (2)
+φ′(y)=N(x,y). (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)=N(x,y)–x+ 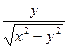 =
= 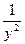 . (3)
. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=  +С=–
+С=– 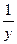 . (4)
. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =
= 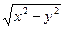 +xy–
+xy– 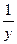 = С. (5)
= С. (5)
Ответ: u(x,y)= 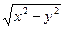 +xy–
+xy– 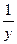 = С – общее решение.
= С – общее решение.
Пример 4–103: Решить ДУ: (2x+ 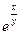 )dx+(1–
)dx+(1– 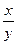 )∙
)∙ 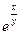 dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =–
=– 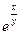 ∙
∙ 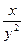 и
и  =–
=– 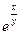 ∙
∙ 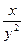 → условие
→ условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 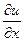 :
:
u(x,y)=  +φ(y)=
+φ(y)= 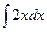 +
+ 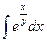 +φ(y)=x2+y
+φ(y)=x2+y 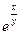 +φ(y). (1)
+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 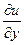 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 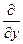 (x2+ y
(x2+ y 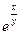 )+φ′(y)=
)+φ′(y)= 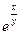 –
– 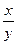
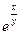 +φ′(y)=N(x,y). (2)
+φ′(y)=N(x,y). (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)=N(x,y)– (1– 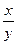 )∙
)∙ 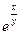 =0. (3)
=0. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=С. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =x2+y
=x2+y 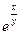 = С. (5)
= С. (5)
Ответ: u(x,y)= x2+y 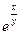 = С – общее решение.
= С – общее решение.
Пример 5–105: Решить ДУ: (siny–ysinx+ 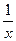 )dx+(xcosy+cosx–
)dx+(xcosy+cosx– 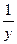 )∙dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
)∙dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =cosy–sinx и
=cosy–sinx и  = cosy–sinx → условие
= cosy–sinx → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 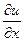 :
:
u(x,y)=  +φ(y)=
+φ(y)= 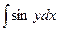 –
– 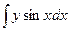 +
+ 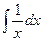 +φ(y)=
+φ(y)=
=xsiny+ycosx+ln|x|+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 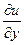 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 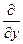 (xsiny+ycosx+ln|x|)+φ′(y)=xcosy+cosx+φ′(y)=N(x,y). (2)
(xsiny+ycosx+ln|x|)+φ′(y)=xcosy+cosx+φ′(y)=N(x,y). (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)=N(x,y)–(xcosy+cosx)= – 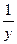 . (3)
. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=–ln|y|. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  = xsiny+ycosx+ln|x|–ln|y|= С. (5)
= xsiny+ycosx+ln|x|–ln|y|= С. (5)
Ответ: u(x,y)= xsiny+ycosx+ln| 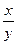 |= С – общее решение.
|= С – общее решение.
Пример 6–143: Решить ДУ: (xcos2y+1)dx–x2∙sin2y∙dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.
Решение:
1). В нашем случае:  =–2x∙sin2y и
=–2x∙sin2y и  =–2x∙sin2y → условие
=–2x∙sin2y → условие  =
=  выполняется → задано уравнение в полных дифференциалах.
выполняется → задано уравнение в полных дифференциалах.
2). Далее решаем уравнение, применяя общий алгоритм:
a0. Находим первообразную функции М = 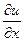 :
:
u(x,y)=  +φ(y)=
+φ(y)= 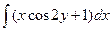 +φ(y)=
+φ(y)= 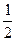 x2cos2y+x+φ(y). (1)
x2cos2y+x+φ(y). (1)
a1. Подберем φ(y) так, чтобы выполнялось условие: 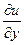 = N(x,y); это значит, что выполняется:
= N(x,y); это значит, что выполняется: 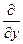 (
( 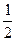 x2cos2y+x)+φ′(y)= –x2∙sin2y+φ′(y)=N(x,y). (2)
x2cos2y+x)+φ′(y)= –x2∙sin2y+φ′(y)=N(x,y). (2)
a2. Используя (2), запишем равенство для вычисления функции φ′(y):
φ′(y)=N(x,y)+ x2∙sin2y=0. (3)
a3. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):
φ(y)=C. (4)
a4. Запишем общее решение заданного уравнения:
u(x,y)=  +
+  =
= 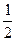 x2cos2y+x= С. (5)
x2cos2y+x= С. (5)
Ответ: u(x,y)= 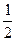 x2cos2y+x= С – общее решение.
x2cos2y+x= С – общее решение.
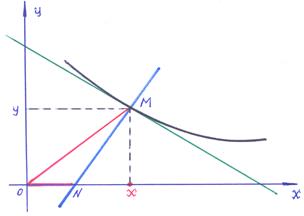
Пример 7–181: Найти уравнение кривой, проходящей через точку (1,2), если произведение абсциссы точки касания на абсциссу точки пересечения нормали с осью ОХ равно удвоенному квадрату расстояния от начала координат до точки касания.
 Решение:
Решение:
Замечание: 1). При составлении дифференциального уравнения необходимо учесть возможные варианты названного в условии равенства: 2|OM|2 = |x∙ON|.
2). Для лучшего восприятия задачи воспользуемся рисунком: отрезки ОМ, ОN и абсцисса точки М выделены красным цветом.
Итак, через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) со свойством:
▪ Случай-1: 2(x2+y2)= x∙(x+yy′); (1)
▪ Случай-2: 2(x2+y2)=–x∙(x+yy′). (2)
Случай-1.
1). Из условия запишем: y′ = 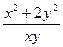 =
= 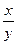 +2
+2 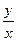 – однородное дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!
– однородное дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!
2). Применим стандартный алгоритм решения задачи:
a1. Исходная запись ДУ решений не дает.
a2. Примем 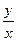 = u; получим: φ(u)=f(u)–u=
= u; получим: φ(u)=f(u)–u= 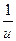 +2u–u=
+2u–u= 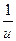 +u=
+u= 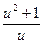 .
.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Дополнительных решений не получим.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): 2 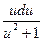 =2
=2 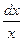 . (3)
. (3)
a5. Интегрируем уравнение (3): ln(u2+1)= lnCx2 → u2+1=Cx2.
a6. Записываем общее решение ДУ. Учитывая что 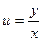 , получаем: y2=x2(Cx2–1).
, получаем: y2=x2(Cx2–1).
a7. Записываем частное решение ДУ, учитывая что интегральная кривая должна пройти через точку (1,2) → С=5 : получаем: y2=x2(5x2–1).
Случай-2.
1). Из условия запишем: y′ =– 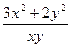 =–3
=–3 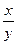 –2
–2 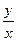 – однородное дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!
– однородное дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!
2). Применим стандартный алгоритм решения задачи:
a1. Исходная запись ДУ решений не дает.
a2. Примем 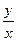 = u; получим: φ(u)=f(u)–u=
= u; получим: φ(u)=f(u)–u= 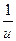 +2u–u=–3
+2u–u=–3 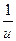 –3u=–3
–3u=–3 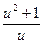 .
.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Дополнительных решений не получим.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): –6 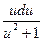 =2
=2 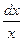 . (3)
. (3)
a5. Интегрируем уравнение (3): –3ln(u2+1)= lnCx2 → u2+1=C 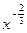 .
.
a6. Записываем общее решение ДУ. Учитывая что 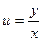 , получаем: y2=x2(C
, получаем: y2=x2(C 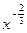 –1).
–1).
a7. Записываем частное решение ДУ, учитывая что интегральная кривая должна пройти через точку (1,2) → С=5 : получаем: y2=x2(5 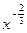 –1).
–1).
Ответ: Случай-1: y2=x2(Cx2–1).– общее решение ДУ, частное решение: y2=x2(5x2–1).
Случай-2: y2=x2(C 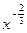 –1).– общее решение ДУ, частное решение: y2=x2(5
–1).– общее решение ДУ, частное решение: y2=x2(5 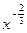 –1)
–1)
Замечание: задачние «зевнул» второе решение!
Пример 8–188: Через сколько времени температура тела, нагретого до 1000С, понизится до 250С, если температура помещения равна 200С и за первые 10 мин тело охладилось до 600С?
Решение:
Замечание: задача интересна «физической стороной» вопроса: физик использует общее решение для определения характеристик остывания конкретного тела в заданных условиях! Общее решение задачи нами получено в Примере 8–187: T=a+(Т0–a)e–kt. (2)
1). Из условия задачи следует: Т0–a=800С, Т–a=400С, t=10 мин.
2). Из уравнения (1) следует: (e–k)10 =0.5 → (e–k)= 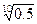 .
.
3). Теперь имеем: Т–a=750С 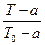 =(
=( 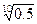 )t, или (
)t, или ( 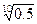 )t =
)t = 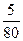 → t ≈40 мин.
→ t ≈40 мин.
Ответ: t ≈ 40 мин.
☻
Вопросы для самопроверки:
1. Как определяют ДУ в полных дифференциалах?
2. Как определить, что данное уравнение есть ДУ в полных дифференциалах?
3. Каков «стандартный алгоритм» решения ДУ в полных дифференциалах?
4. Что такое «интегрирующий множитель уравнения»?
5. Привести пример применения ДУ для решения задачи из геометрии.
6. Привести пример применения ДУ для решения задачи из физики.
< * * * * * >
