Одноканальная СМО с ожиданием и неограниченной очередью

Перейдем теперь к рассмотрению одноканальной СМО с ожиданием без ограничения на вместимость блока ожидания (т.е. Ν → ∞). Остальные условия функционирования СМО остаются без изменений.

Устойчивое решение в такой системе существует только тогда, когда λ<μ, то есть заявки должны обслуживаться с большей скоростью, чем поступают, в противном случае очередь может разрастись до бесконечности.

Вероятность того, что в системе находится п заявок, вычисляется по формуле

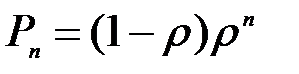, n=0,1,2,…,

где 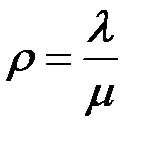<1.

Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:

среднее число находящихся в системе клиентов (заявок) на обслуживание:

;

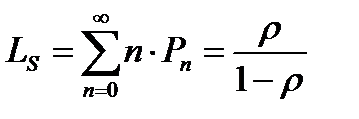средняя продолжительность пребывания клиента в системе:

;

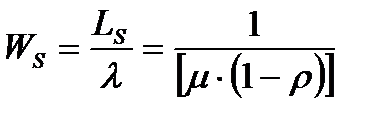среднее число клиентов в очереди на обслуживание:

;

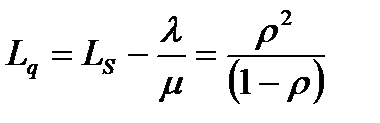средняя продолжительность пребывания клиента в очереди:

;

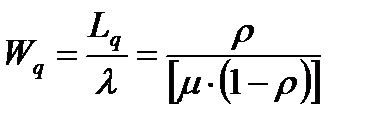Пример 9.3. Вспомнив о ситуации, рассмотренной в примере 9.2, где речь идет о функционировании окна оформления в зоне таможенного контроля. Пусть рассматриваемое зона таможенного контроля в пункте пропуска располагает неограниченным количеством площадок для стоянки прибывающих на оформление автомобилей, т.е. длина очереди не ограничена.

Требуется определить финальные значения следующих вероятностных характеристик:

1. вероятности состояний системы (окна оформления);

2. среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);

3. среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);

4. среднее число автомобилей в очереди на обслуживании;

5. среднюю продолжительность пребывания автомобиля в очереди.

Решение.

Параметр потока обслуживания и приведенная интенсивность потока автомобилей ρ определены в предыдущем примере:

μ=0,952; ρ=0,893.

Вычислим предельные вероятности системы по формулам

P₀=1- ρ =1-0,893=0,107;

P₁=(1- ρ)· ρ =(1-0,893)·0,893=0,096;

P₂=(1- ρ)· ρ ²=(1-0,893)·0,893²=0,085;

P₃=(1- ρ)· ρ ³=(1-0,893)·0,893³=0,076;

P₄=(1- ρ)· ρ ⁴=(1-0,893)·0,893⁴=0,068;

P₅=(1- ρ)· ρ ⁵=(1-0,893)·0,893⁵=0,061 и т.д.

Следует отметить, что Р₀ определяет долю времени, в течение которого окно оформления вынужденно бездействует (простаивает). В нашем примере она составляет 10, 7%, так как Р₀=0,107. Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди):

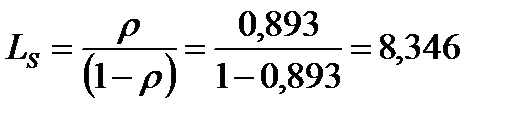ед.

Средняя продолжительность пребывания клиента в системе:

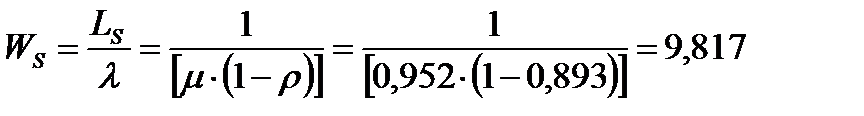час.

Среднее число автомобилей в очереди на обслуживание:

.

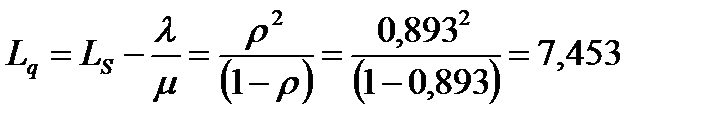Средняя продолжительность пребывания автомобиля в очереди:

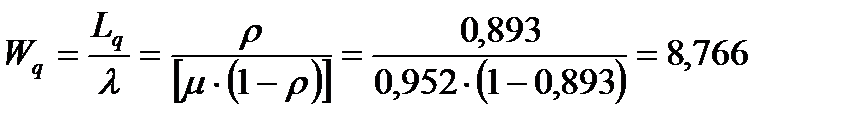час.

Относительная пропускаемая способность системы равна единицы, так как все поступившие заявки рано или поздно будут обслужены: q=1.

Абсолютная пропускная способность:

A=λ∙q=0,85∙1=0,85.

Следует отметить, что пункт таможенного контроля, осуществляющий оформления автомобилей, прежде всего интересует количество клиентов, которое посетит окно оформления при снятии ограничения на длину очереди.

Допустим, в первоначальном варианте количество мест для стоянки прибывших автомобилей как в предыдущем примере было равно трем. Частота m возникновения ситуаций, когда прибывающий на пункт оформления автомобиль не имеет возможности присоединиться к очереди:

m=λ∙P_N.

В нашем примере при N=3+1=4 и ρ =0,893,

m=λ∙P₀∙ ρ ⁴=0,85∙0,248∙0,8934=0,134 автомобиля в час.

При 12-часовом режиме работы окна оформления это эквивалентно тому, что окно оформления в среднем за смену (день) будет терять 12∙0,134=1,6 автомобиля.

Снятие ограничения на длину очереди позволяет увеличить количество обслуживаемых клиентов в нашем примере в среднем на 1,6 автомобиля за смену (12 ч. работы) пункта оформления. Ясно, что решение относительно расширения площади для стоянки автомобилей, прибывающих в зону таможенного контроля, должно основываться на оценке экономического ущерба, который обусловлен потерей клиентов при наличие всего трех мест для стоянки этих автомобилей.