| | | Даны точки М1(2; -3; 6), M2(0; 7; 0), M3(3; 2; -4), M4( 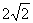 ; 4; -5), M5(1; -4; -4), M6(2; 6; ; 4; -5), M5(1; -4; -4), M6(2; 6; 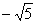 ). Установить, какие из них лежат на поверхности, определенной уравнением ). Установить, какие из них лежат на поверхности, определенной уравнением 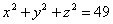 , и какие не лежат на ней? Какая поверхность определена данным уравнением? , и какие не лежат на ней? Какая поверхность определена данным уравнением?  | |
| | | На поверхности 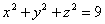 найти точку, для которой: 1). Абсцисса равна , ордината рана 2; 2). Абсцисса равна 2, ордината равна 5, 3). Абсцисса равна 2, апликата равна 2; 4). Ордината равна 2, апликата равна 4. найти точку, для которой: 1). Абсцисса равна , ордината рана 2; 2). Абсцисса равна 2, ордината равна 5, 3). Абсцисса равна 2, апликата равна 2; 4). Ордината равна 2, апликата равна 4. 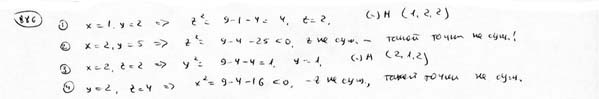 |
| | | Установить, какие геометрические образы определяются следующими уравениями в декартовых прямоугольных координатах пространства: |
| | 887.1 | 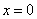 ; ; |
| | 887.2 | 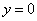 ; ; |
| | 887.3 | 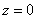 ; ; |
| | 887.4 | 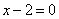 ; ; |
| | 887.5 | 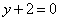 ; ; |
| | 887.6 | 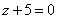 ; ; |
| | 887.7 | 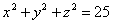 ; ; |
| | 887.8 | 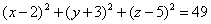 ; ; |
| | 887.9 | 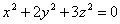 ; ; |
| | 887.10 | 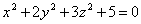 ; ; |
| | 887.11 | 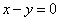 ; ; |
| | 887.12 | 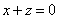 ; ; |
| | 887.13 | 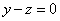 ; ; |
| | 887.14 | 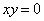 ; ; |
| | 887.15 | 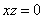 ; ; |
| | 887.16 | 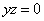 ; ; |
| | 887.17 | 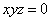 ; ; |
| | 887.18 | 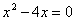 ; ; |
| | 887.19 | 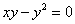 ; ; |
| | 887.20 | 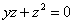 . . 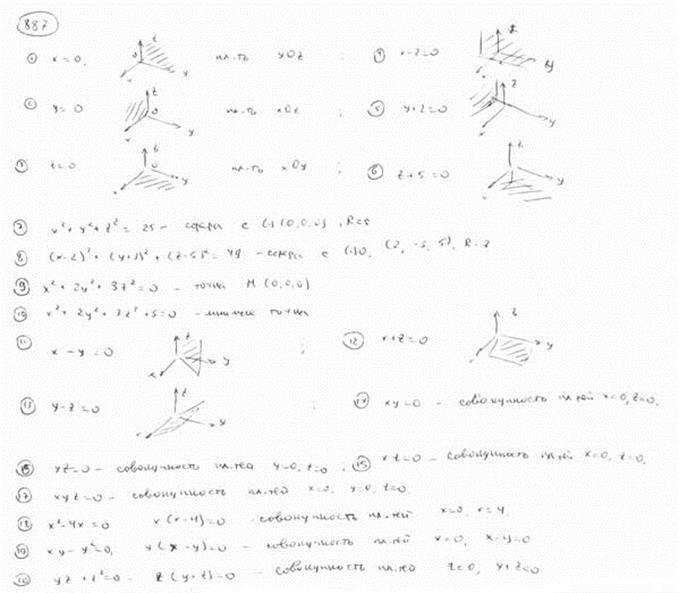 |
| | | Даны две точки F1(-c; 0; 0) и F2(c; 0; 0). Вывести уравнение геометрического места точек, сумма расстояний от которых до двух данных точек есть величина постоянная, равная 2а при условии a>0, c>0; a>c. Задача 0888 Даны две точки F1(—с; 0; 0) и F2(c; 0; 0). Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек есть величина постоянная, равная 2а при условии а>0, с>0; а>с.. Р е ш е н и е. Обозначим буквой М произвольную точку пространства, буквами х, у, z — её координаты. Так как точка М может занимать любое положение, то х, у и z являются переменными величинами; их называют текущими координатами. Точка М лежит на данной поверхности в том и только в том случае, когда MF1 + MF2 = 2a (1) Это есть определение поверхности, выраженное символически. Выразим MF1 и MF2 — через текущие координаты точки М: MF1 = 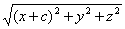 , MF2 = . , MF2 = . 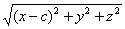 Подставим полученные выражения в равенство (1). Тем самым мы найдём уравнение Подставим полученные выражения в равенство (1). Тем самым мы найдём уравнение 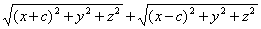 (2) которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности. Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде. Уединим в уравнении (2) первый радикал: (2) которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности. Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде. Уединим в уравнении (2) первый радикал: 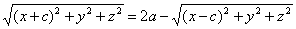 возведём обе части этого равенства в квадрат и раскроем скобки; мы получим: x2 + 2cx+с2+y2 + z2 =4а2 — 4а возведём обе части этого равенства в квадрат и раскроем скобки; мы получим: x2 + 2cx+с2+y2 + z2 =4а2 — 4а 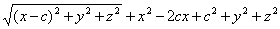 или а или а 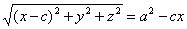 Снова, освобождаясь от радикала, найдём: a2x2 — 2a2cx + а2с2 + a2 y2 + a2 z2 = a4 — 2а2сх + с2x2, или (а2 — с2) х2 + a2y2 + a222 = а2 (а2 — с2). (3) Так как а > с, то а2 — с2 > 0; положительное число a2 — с2 обозначим через b2. Тогда уравнение (3) примет вид b2x2 + а2y + a2z2 = a2b2 или Снова, освобождаясь от радикала, найдём: a2x2 — 2a2cx + а2с2 + a2 y2 + a2 z2 = a4 — 2а2сх + с2x2, или (а2 — с2) х2 + a2y2 + a222 = а2 (а2 — с2). (3) Так как а > с, то а2 — с2 > 0; положительное число a2 — с2 обозначим через b2. Тогда уравнение (3) примет вид b2x2 + а2y + a2z2 = a2b2 или 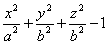 Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида. Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида. |
| | | Вывести уравнение сферы, центр которой находится в начале координат и радиус которой равен r. 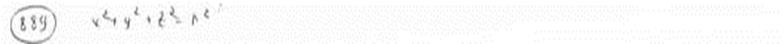 |
| | | Вывести уравнение сферы, центр которой C( 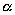 , , 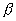 , , 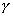 ) и радиус которой равен r. ) и радиус которой равен r. 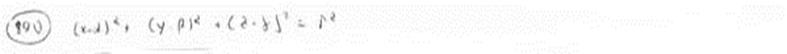 |
| | | Из точки P(2; 6; -5) проведены всевозможные лучи до пересечения с плоскостью Oxz. Составить уравнение геометрического места их середин.  |
| | | Из точки А(3; -5; 7) проведены всевозможные лучи до пересечения с плоскостью Oxy. Составить уравнение геометрического места их середин. 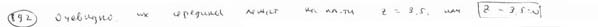 |
| | | Из точки С(-3; -5; 9) проведены всевозможные лучи до пересечения с плоскостью Oyz. Составить уравнение геометрического места их середин. 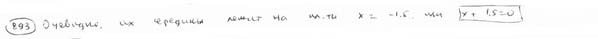 |
| | | Вывести уравнение геометрического места точек, разность квадратов расстояний от которых до точек F1(2; 3; -5), F2(2; -7; -5) есть величина постоянная, равная 13. 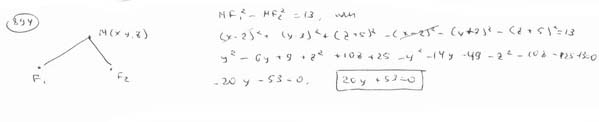 |
| | | Вывести уравнение геометрического места точек, сумма квадратов расстояний от которых до двух точек F1(-a; 0; 0), F2(a; 0; 0) равна постоянной величине 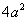 . . 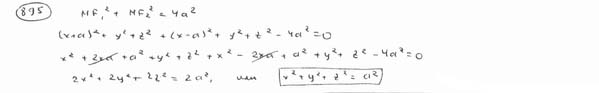 |
| | | Вершины куба суть точки A(-a; -a; -a), B(a; -a; -a), C(-a; a; -a), D(a; a; a). Составить уравнение геометрического места точек, сумма квадратов расстояний от которых до граней этого куба есть величина постоянная, равная 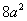 . .  |
| | | Вывести уравнение геометрического места точек, равноудаленных от двух точек M1(1; 2; -3), M2(3; 2; 1). 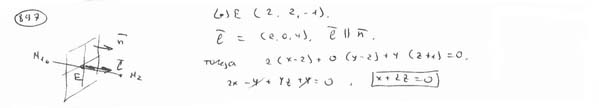 |
| | | Вывести уравнение геометрического места точек, сумма расстояний от которых до двух даных точек F1(0; 0; -4), F2(0; 0; 4) есть величина постоянная, равная 10. 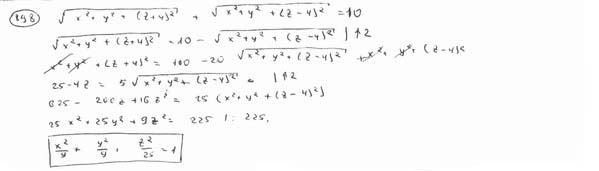 |
| | | Вывести уравнение геометрического места точек, разность расстояний от которых до двух данных точек F1(0; -5; 0), F2(0; 5; 0) есть величина постоянная, равная 6. 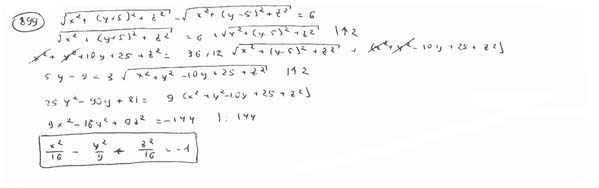 Глава 36. Уравнения линии. Задача о пересечении трех поверхностей Глава 36. Уравнения линии. Задача о пересечении трех поверхностей | | | Даны точки M1(3; 4; -4), M2(-3; 2; 4), M3(-1; -4; 4), M4(2; 3; -3). Определить, какие из них лежат на линии 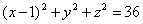 , , 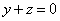 и какие не лежат на ней. и какие не лежат на ней. 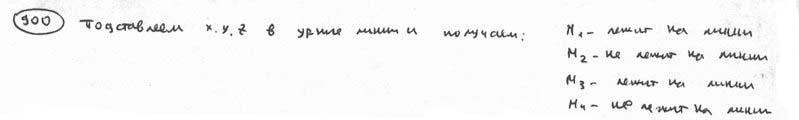 | | | | Определить, какие из следующих линий проходят через начало координат: | | | 901.1 | 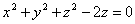 , , 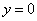 ; ; | | | 901.2 | 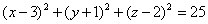 , , 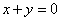 ; ; | | | 901.3 | 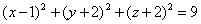 , , 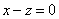 . . 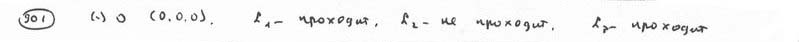 | | | | На линии 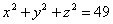 , , 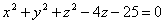 найти точку: найти точку: | | | 902.1 | абсцисса которой равна 3; | | | 902.2 | ордината которой равна 2; | | | 902.3 | апликата которой равна 8.  | | | | Установить, какие линии определяются следующими уравнениями: | | | 903.1 | 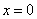 , , 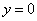 ; ; | | | 903.2 | 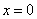 , , 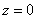 ; ; | | | 903.3 | 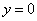 , , 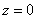 ; ; | | | 903.4 | 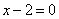 , , 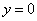 ; ; | | | 903.5 | 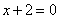 , , 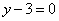 ; ; | | | 903.6 | 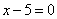 , , 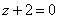 ; ; | | | 903.7 | 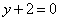 , , 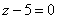 ; ; | | | 903.8 | 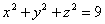 , , 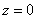 ; ; | | | 903.9 | 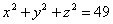 , , 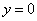 ; ; | | | 903.10 | 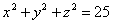 , , 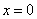 ; ; | | | 903.11 | 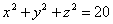 , , 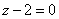 . .  | | | | Составить уравнения линии пересечения плоскости Oxz и сферы с центром в начале координат и радиусом, равным 3.  | | | | Составить уравнения линии пересечения сферы, центр которой находится в начале координат и радиус раен 5, с плоскостью, параллельной плоскости Oxz и лежащей в левом полупространстве на расстоянии двух единиц от нее.  | | | | Составить уравненя линии пересечения плоскости Oyz и сферы, центр которой находится в точке С(5; -2; 1) и радиус равен 13. 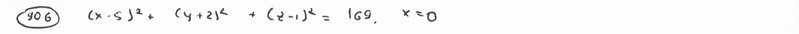 | | | | Составить уравнения линии пересечения двух сфер, одна из которых имеет радиус, равный 6, и центр в начале координат; другая имеет радиус, равный 5, и центр С(1; -2; 2).  | | | | Найти точки пересечения поверхностей 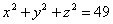 , , 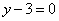 , , 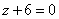 . . 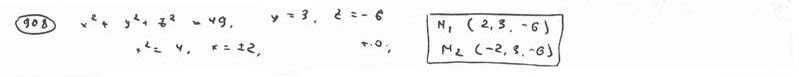 | | | | Найти точки пересечения поверхностей 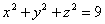 , , 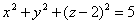 , , 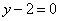 . .  | |
| | | | | | |
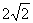 ; 4; -5), M5(1; -4; -4), M6(2; 6;
; 4; -5), M5(1; -4; -4), M6(2; 6; 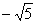 ). Установить, какие из них лежат на поверхности, определенной уравнением
). Установить, какие из них лежат на поверхности, определенной уравнением 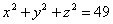 , и какие не лежат на ней? Какая поверхность определена данным уравнением?
, и какие не лежат на ней? Какая поверхность определена данным уравнением? 
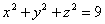 найти точку, для которой: 1). Абсцисса равна , ордината рана 2; 2). Абсцисса равна 2, ордината равна 5, 3). Абсцисса равна 2, апликата равна 2; 4). Ордината равна 2, апликата равна 4.
найти точку, для которой: 1). Абсцисса равна , ордината рана 2; 2). Абсцисса равна 2, ордината равна 5, 3). Абсцисса равна 2, апликата равна 2; 4). Ордината равна 2, апликата равна 4. 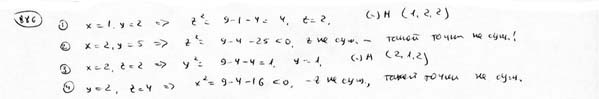
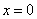 ;
; 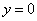 ;
; 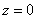 ;
; 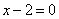 ;
; 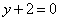 ;
; 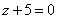 ;
; 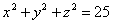 ;
; 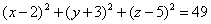 ;
; 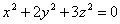 ;
; 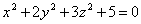 ;
; 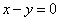 ;
; 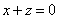 ;
; 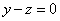 ;
; 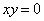 ;
; 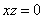 ;
; 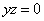 ;
; 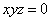 ;
; 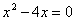 ;
; 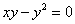 ;
; 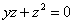 .
. 
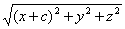 , MF2 = .
, MF2 = . 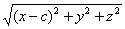 Подставим полученные выражения в равенство (1). Тем самым мы найдём уравнение
Подставим полученные выражения в равенство (1). Тем самым мы найдём уравнение 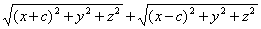 (2) которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности. Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде. Уединим в уравнении (2) первый радикал:
(2) которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности. Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде. Уединим в уравнении (2) первый радикал: 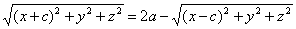 возведём обе части этого равенства в квадрат и раскроем скобки; мы получим: x2 + 2cx+с2+y2 + z2 =4а2 — 4а
возведём обе части этого равенства в квадрат и раскроем скобки; мы получим: x2 + 2cx+с2+y2 + z2 =4а2 — 4а 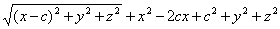 или а
или а 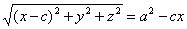 Снова, освобождаясь от радикала, найдём: a2x2 — 2a2cx + а2с2 + a2 y2 + a2 z2 = a4 — 2а2сх + с2x2, или (а2 — с2) х2 + a2y2 + a222 = а2 (а2 — с2). (3) Так как а > с, то а2 — с2 > 0; положительное число a2 — с2 обозначим через b2. Тогда уравнение (3) примет вид b2x2 + а2y + a2z2 = a2b2 или
Снова, освобождаясь от радикала, найдём: a2x2 — 2a2cx + а2с2 + a2 y2 + a2 z2 = a4 — 2а2сх + с2x2, или (а2 — с2) х2 + a2y2 + a222 = а2 (а2 — с2). (3) Так как а > с, то а2 — с2 > 0; положительное число a2 — с2 обозначим через b2. Тогда уравнение (3) примет вид b2x2 + а2y + a2z2 = a2b2 или 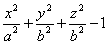 Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида.
Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида. 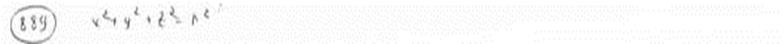
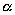 ,
, 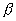 ,
, 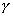 ) и радиус которой равен r.
) и радиус которой равен r. 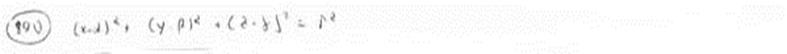

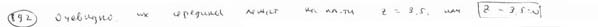
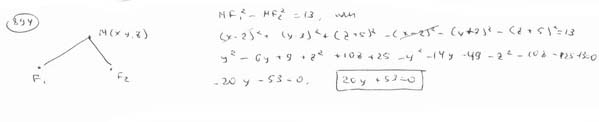
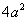 .
. 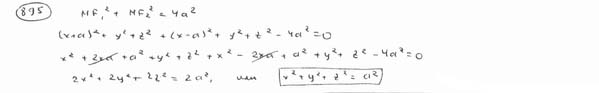
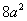 .
. 
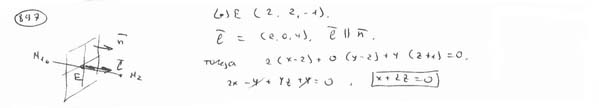
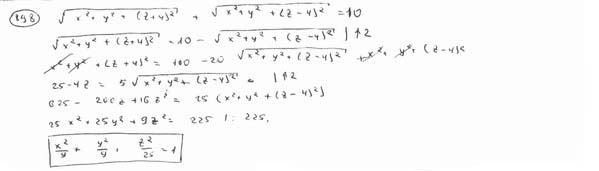
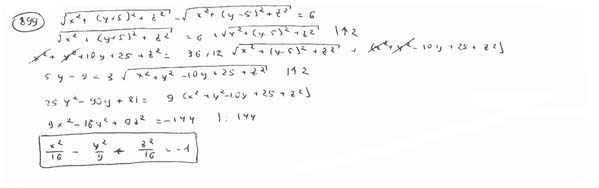 Глава 36. Уравнения линии. Задача о пересечении трех поверхностей
Глава 36. Уравнения линии. Задача о пересечении трех поверхностей 
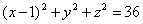 ,
, 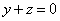 и какие не лежат на ней.
и какие не лежат на ней. 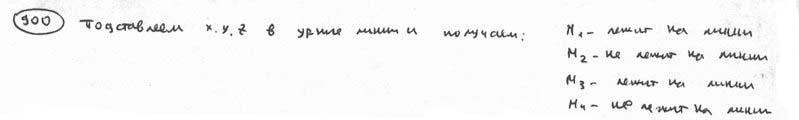
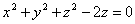 ,
, 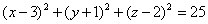 ,
, 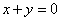 ;
; 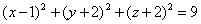 ,
, 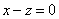 .
. 
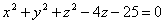 найти точку:
найти точку: 
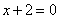 ,
, 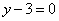 ;
; 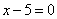 ,
, 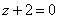 ;
; 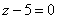 ;
; 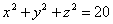 ,
, 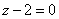 .
. 


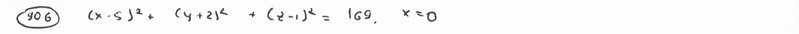

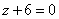 .
. 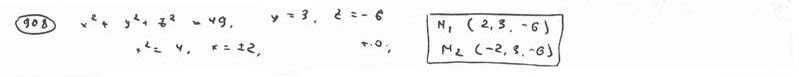
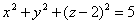 ,
, 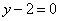 .
. 