Пример расчета системы с одной степенью свободы

Условие задачи[21]

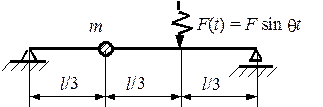Рис. 7.2. Балка с одной степенью свободы под действием возмущающей силы

На балку с сосредоточенной массой 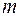действует возмущающая нагрузка 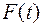(рис. 7.2). Требуется построить эпюру изгибающих моментов от динамического действия нагрузки. Примем следующие исходные данные: 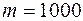кг, жесткость балки 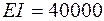кН×м², ее длина 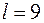м, отношение частоты вынужденных колебаний к частоте собственных колебаний 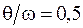, амплитудное значение возмущающей нагрузки 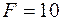кН.

Решение

Найдем частоту свободных колебаний по формуле (7.1). Перемещение 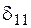ищем методом Максвелла – Мора:

.

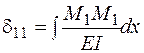Для построения эпюры изгибающих моментов 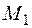приложим в точке, где расположена сосредоточенная масса, единичную силу по направлению возможного перемещения массы. В данном примере сосредоточенная масса может перемещаться только по вертикали. Эпюра моментов от единичной силы показана на рис. 7.3, а. Интегрирование формулы Максвелла – Мора по правилу Верещагина дает

= .

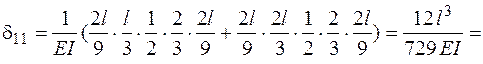
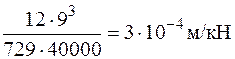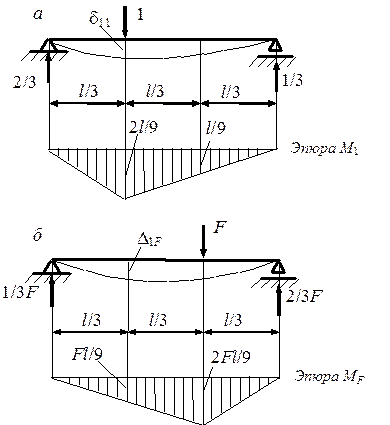Рис. 7.3. Эпюры изгибающих моментов: а – от единичной силы; б – от амплитудного значения вынуждающей нагрузки F

Обратите внимание на единицы измерения величины 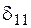. Подставим 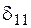в формулу (7.1). Вспомним, что 1 кН = 10³ Н = 10³ кг×м / с², после подстановки массы 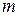в кг получим круговую частоту свободных колебаний в с^–1:

.

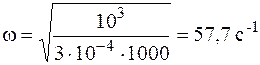Теперь определим амплитудное значение силы инерции, используя формулу (7.2). Чтобы воспользоваться этой формулой, найдем величину 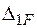– перемещения по направлению движения массы от амплитудного значения силы 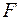. В соответствии с методом Максвелла – Мора это перемещение

.

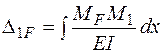Эпюра 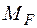от действия амплитудного значения 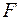показана на рис. 7.3, б. Перемножая эпюры 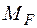и 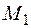по правилу Верещагина, найдем

.

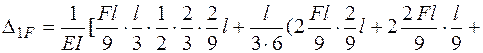
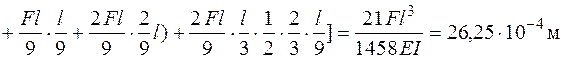Частота вынужденных колебаний согласно условию

.

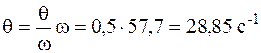Тогда амплитудное значение силы инерции по формуле (7.2)

.

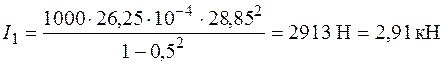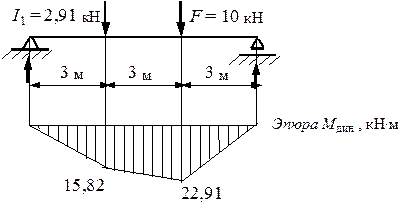Рис. 7.4. Эпюра изгибающих моментов от динамического действия нагрузки

Окончательная эпюра изгибающих моментов от динамического действия нагрузки, построенная с учетом формулы (7.3), показана на рис. 7.4.

РАСЧЕТ РАМЫ (БАЛКИ) НА УДАРНУЮ НАГРУЗКУ (ЗАДАЧА № 38)

Основные определения

Влияние ударной нагрузки на напряжения и деформации конструкции оценивается с помощью динамического коэффициента 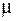, который можно определить по следующей формуле:

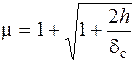, (7.4)

где h – высота падения груза; 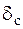– вертикальное перемещение точки приложения груза при статическом его приложении.

Формула (7.4) является достаточно грубой оценкой влияния ударной нагрузки, так как она получена с использованием ряда упрощающих задачу допущений. Одним из этих допущений является предположение о том, что материал конструкции в момент удара работает в упругой стадии (подчиняется закону Гука). Зная динамический коэффициент, можно найти динамические (возникающие под действием ударной нагрузки) напряжения 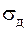в конструкции по формуле

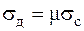, (7.5)

где 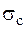– напряжения от статического (медленного) приложения нагрузки. В 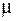раз (справедлив закон Гука) увеличиваются и деформации конструкции от ударной нагрузки по сравнению со статическими деформациями.

В процессе вычисления напряжений по (7.5) необходимо следить, чтобы полученные динамические напряжения не превосходили величину предела пропорциональности материала, так как в этом случае пользоваться формулой (7.4) нельзя. Если все же динамические напряжения оказались больше предела пропорциональности, необходимо предусмотреть конструктивные меры по увеличению статического перемещения, например сделать опорные закрепления балки (рамы) податливыми, поставив специальные прокладки. Увеличение 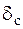приведет к уменьшению динамического коэффициента[22].