Задачи для контрольной работы
Введение.
Общий курс высшей математики, изучаемой студентами-заочниками инженерно-технических и технологических специальностей, состоит из аналитической геометрии с элементами линейной алгебры, математического анализа, элементов теории вероятности и математической статистики.
Этот курс ставит основной своей задачей сообщить студенту сведения о высшей математике, необходимые для успешного изучения общетеоретических и специальных дисциплин, и также развить навыки логического мышления.
Учебный материал по курсу высшей математики распределен на пять первых семестров. В конце каждого семестра предусмотрен зачет или экзамен по изученным разделам математики. Соответственно этим разделам студенты выполняют контрольные работы согласно учебному плану своей специальности.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. Лекции, практические, индивидуальные межсессионные занятия призваны помочь им в самостоятельной работе и выполнении контрольных работ.
Работа студента-заочника над учебным материалом по математики состоит из следующих элементов: слушание лекций, участие в практических занятиях, участие в межсессионных индивидуальных занятиях, изучение материала по учебникам, решение задач, ответы на вопросы для самоконтроля, выполнение контрольных работ (1-5 в семестр), сдача зачетов и экзаменов.
Настоящий сборник содержит все задания для выполнения контрольных работ по высшей математике а также ставит цель помочь студенту-заочнику самостоятельно работать над учебным материалом по высшей математике, в нем перечислена литература, рекомендованная для самостоятельного изучения материала, содержится программа по всему курсу, методика изучения и решения типовых вариантов контрольных работ.
Контрольная работа №1
Линейная алгебра. Аналитическая геометрия на плоскости и в пространстве. Введение в анализ. Производная.
Решение типового варианта.
Задача 1.Вычислить определитель.
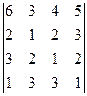
Решение:Разложим определитель по первой строке.
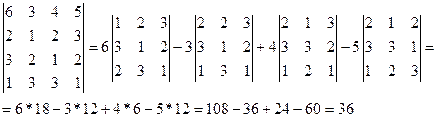
Для вычисления определителя пятого порядка разложить его по элементам первой строки, получим два определителя четвертого порядка, которые вычисляются аналогично.
Задача 2.Найдите сумму 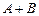 , разность
, разность 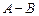 , произведения
, произведения 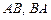 матриц
матриц  и
и  , если это возможно
, если это возможно
Воспользоваться формулами
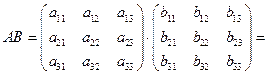
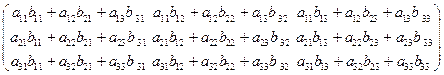
При сложении (вычитании) матриц соответствующие компоненты суммируются (вычитаются).
Задача 3.Даны векторы 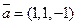
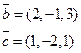
Проверить, что векторы 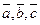 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 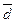 в этом базисе
в этом базисе 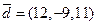 . Вычислить скалярное и векторное произведение векторов
. Вычислить скалярное и векторное произведение векторов 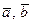 .
.
Решение:Поскольку смешанное произведение
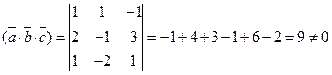
то векторы 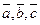 образуют базис.
образуют базис.
Вектор 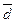 можно представить в виде
можно представить в виде 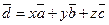 .
.
Это равенство равносильно следующим равенствам:
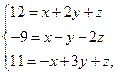
т.к. равные векторы имеют равные координаты и координаты линейной координации векторов равны соответствующим линейным комбинациям одноименных координат.
Решив данную систему методом Гаусса, имеем
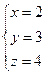
Итак, 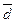 в данном базисе имеет координаты
в данном базисе имеет координаты 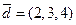
Скалярное произведение: 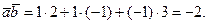
Векторное произведение:
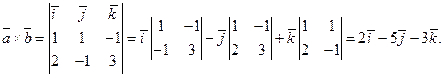
Задача 4.
Решить систему
а) методом Крамера
б) матричным методом
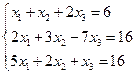
Решение:
а) Вычислим определители
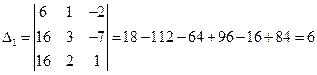
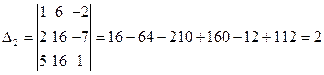
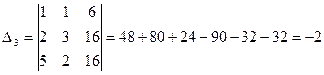
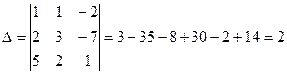
По формулам Крамера, имеем
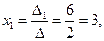
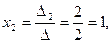
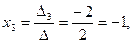
б) Найдем алгебраические дополнения
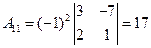
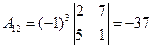
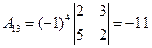
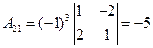
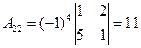
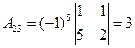
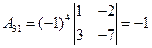
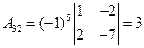
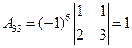
Обратная матрица
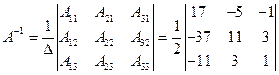
Находим 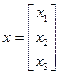
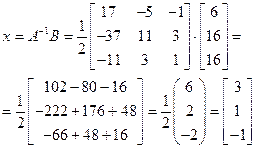
таким образом 
Задача 5.Исследовать систему на совместность методом Гаусса, если система совместна – найти ее решение.
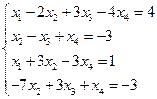
Решение:Составим расширенную матрицу системы:
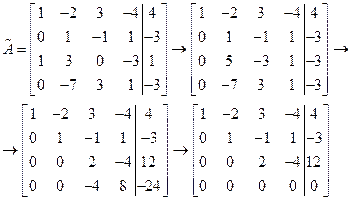
Ранг матрицы системы совпадает с рангом расширенной матрицы, поэтому на основании теоремы Кронекера-Капелли заключаем, что система совместна. Найдем ее решение.
Исходная система равносильна следующей:
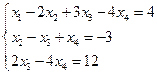
Пусть 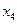 - свободная переменная, а
- свободная переменная, а 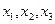 - базисные переменные, тогда
- базисные переменные, тогда
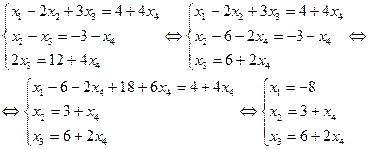
Полагая 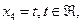 получаем
получаем
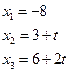
Итак, система имеет бесконечное множество решений: 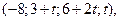
Задача 6.Даны координаты вершин 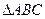 . Найдите
. Найдите
а) длину стороны АВ
б) уравнение высоты СD и ее длину
в) уравнение медианы АМ
г) точку пересечения высоты СD и медианы АМ
д) угол С в 
А(3,4) В(8,10) С(5,-4)
Решение:
а) 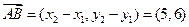
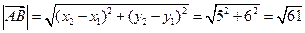
б) Составим уравнение прямой АВ с помощью формулы
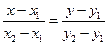
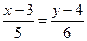
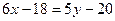
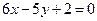 - уравнение прямой АВ
- уравнение прямой АВ
Уравнение высоты СD можно записать как уравнение прямой, проходящей через точку С и перпендикулярной к прямой АВ, имеющей нормальный вектор 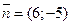 , который для этой прямой будет направляющим
, который для этой прямой будет направляющим 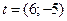
СD: 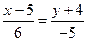
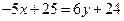
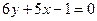
Найдем точку Д, как точку пересечения прямых СД и АВ
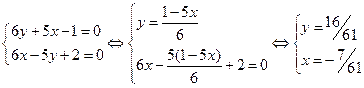
в) Медиана делит стороны ВС пополам, поэтому из формул середины отрезка
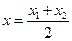
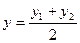
находим координаты точки М
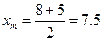
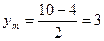
M (7.5;3)
Уравнение прямой АМ:
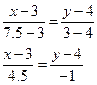
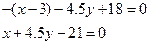
г) Точку пересечения находим из системы
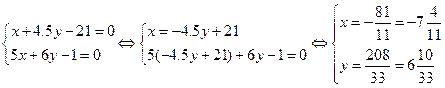
Значит, m пересечения 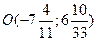
Задача 7.Даны четыре точки А(4,2,5), В(0,7,2), С(0,2,7) и S(1,5,0).
Найти: уравнения
а) плоскость АВС
б) прямой АВ
в) прямой SN, перпендикулярной к плоскости АВС
г) косинус угла между плоскостями АВС и ВСS
д) объем пирамиды АВСS
е) уравнение прямой SD параллельной прямой АВ
ж) площадь грани АВС
Решение:
а) Уравнение плоскости, проходящей через 3 точки
Принимает вид:
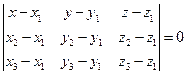 ,
, 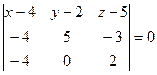
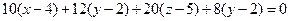
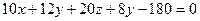
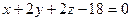
б) Уравнение прямой АВ, как прямой, проходящей через две точки, запишется так
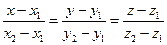
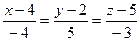
в) Уравнение высоты SN, опущенной из вершины S на плоскость АВС можно записать как уравнение прямой, проходящей через точку S и перпендикулярной плоскости АВС, имеющей нормальный вектор 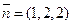 , который для этой прямой будет направляющим
, который для этой прямой будет направляющим
SN: 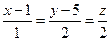 или
или
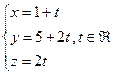
г) Найдем уравнение плоскости ВСS
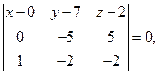
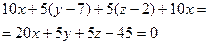
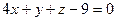
Косинус угла найдем по формуле
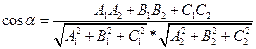
Отсюда
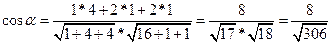
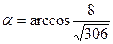
д) Объем пирамиды
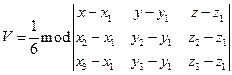
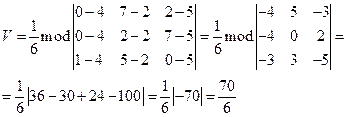
е) Т.к. прямая SД параллельна АВ, то направляющие векторы прямых совпадают 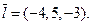 Составим уравнение прямой SД, проходящий через точку S(1,5,0)
Составим уравнение прямой SД, проходящий через точку S(1,5,0)
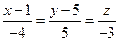
ж) Площадь грани вычислим по формуле
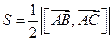
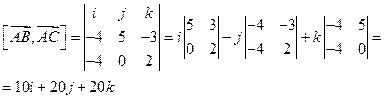
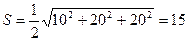
Задача 8.Методом параллельных сечений исследовать форму поверхности
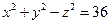
Решение:Будем пересекать поверхность горизонтальными плоскостями 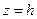 .
.
Подставим 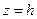 в уравнение. Получим
в уравнение. Получим

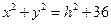
Откуда видно, что любом таком сечении получаются окружности радиуса 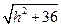 , наименьшая из которых имеет радиус равный 6(h=0). Сечение плоскостями x=с дает гиперболы
, наименьшая из которых имеет радиус равный 6(h=0). Сечение плоскостями x=с дает гиперболы
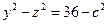
Сечение плоскостями 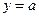 , также дает гиперболы
, также дает гиперболы
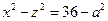
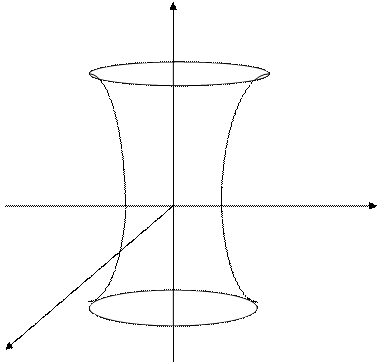
Координатные плоскости являются плоскостями симметрии. Поверхность изображена на рисунке
Задача 9:Найти предел функции не пользуясь правилом Лопиталя.
Решение:
а)
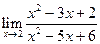 =
= 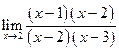 =
= 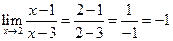
б)
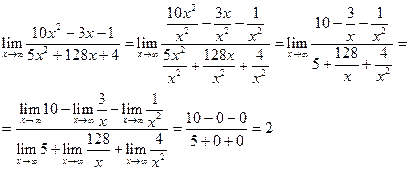
в)
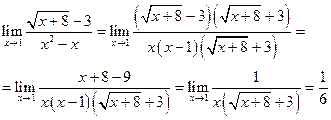
г)
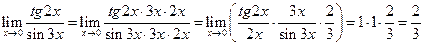
д)
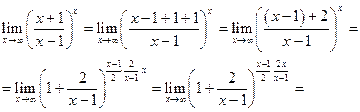
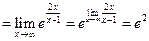
Задача 10.Найти производную заданной функции
а) 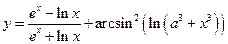
б) 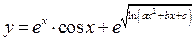
в) 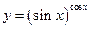
г) 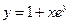
Решение:
Применяя правила дифференцирования и используя таблицу производных, находим:
а) 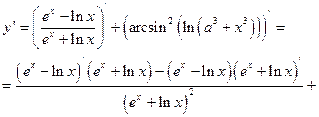
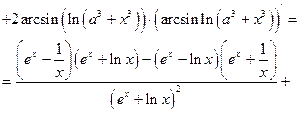
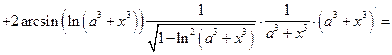
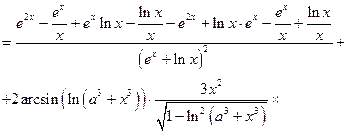
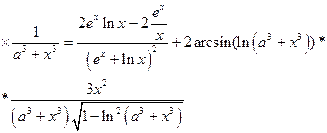
б)
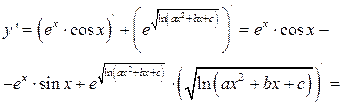
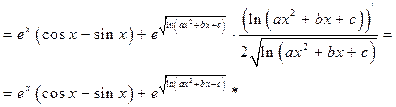
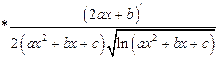
в) 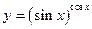
Прологарифмируем обе части:
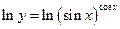
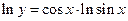
Продифференцируем обе части
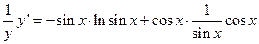
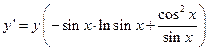
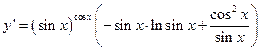
г) Дифференцируя обе части равенства, имеем
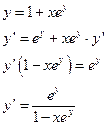
Т.к. по условию 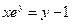 , то получаем
, то получаем
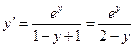
Задача 11.Дана функция 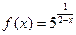 в точке
в точке 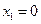 и
и 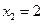
а) Установить является ли функция непрерывной в этих точках
б) Найти пределы слева и справа
в) Сделать схематический чертеж
Решение:
В точке x = 0 функция непрерывна, т.е.
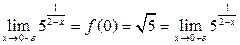
В точке x = 2
предел слева
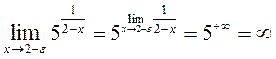
предел справа
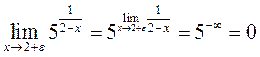
Схематичный чертеж на рис 1
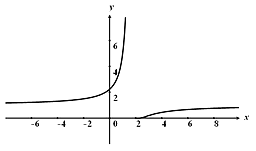
Рисунок 1
Задача 12.
 x + 1, если x ≤ 0
x + 1, если x ≤ 0
Дана функция y = x2, если 0 > x ≤ 2
½ x + 3 , если x ≥ 2
Найти точки разрыва, если они существуют сделать чертеж.
Решение:
График функции изображен на рисунке
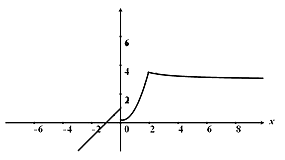
В точке x = 0 разрыв первого рода т.к. 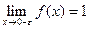
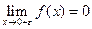
В точке x = 2 разрыва нет. 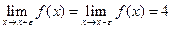
В остальных точках функция непрерывна.
Задача 13.
a) С помощью преобразования графика функции 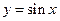 построить функцию
построить функцию 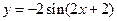
Решение:
От функции 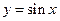 к функции
к функции 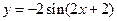 можно перейти с помощью следующей цепочки преобразований:
можно перейти с помощью следующей цепочки преобразований: 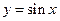
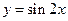
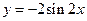
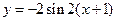
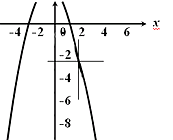
На рисунке изображены соответствующие графики:
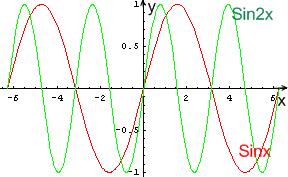
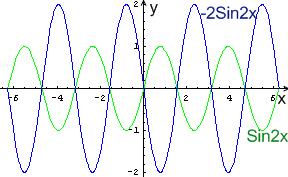
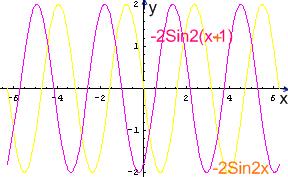
б) Построить по точкам график функции
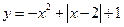
Решение:
Рассмотрим два случая
1) x – 2 ≥ 0 x ≥ 2 тогда 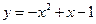
2) x – 2 < 0 x < 2 тогда 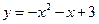 строим график
строим график
Задача 14.Используя правило Лопиталя вычислить пределы:
а) 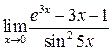
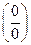
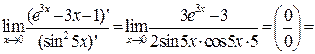
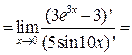
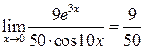
б)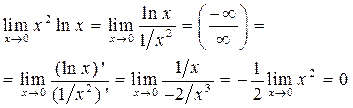
в) 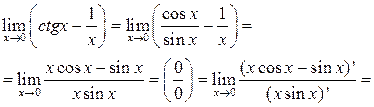
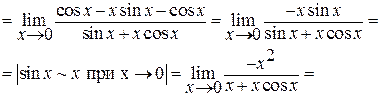
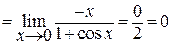
г)
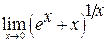
Имеем неопределённость вида 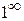 . Положим
. Положим 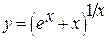 и прологарифмируем обе части равенства
и прологарифмируем обе части равенства 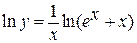
Найдём
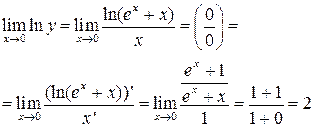
Поскольку 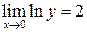 , то
, то 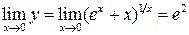
Задача 15. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить её график: 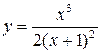
Решение: Приведём схему полного исследования функции
1. Область определения функции
2. Чётность, нечётность, переодичность
3. Точки разрыва функции; приделы при 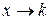 концам промежутков области определения; асимптоты
концам промежутков области определения; асимптоты
4. Интервалы возрастания и убывания функции, точки экстремума; вычислить значения экстремумов
5. Интервалы выпуклости и точки перегиба
6. Точки пересечения графика с осями координат
7. График
1. Функция 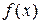 определена, если
определена, если 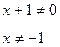 , значит
, значит 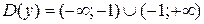
2. Т.к. область определения функции 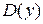 не является симметричным множеством относительно начала координат, то функция
не является симметричным множеством относительно начала координат, то функция 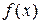 не может быть чётной, нечётной и периодической.
не может быть чётной, нечётной и периодической.
3. Найдём пределы функций при 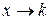 концам промежутков области определения
концам промежутков области определения
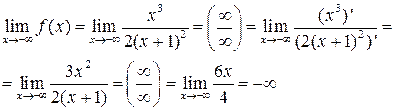
Аналогично, получаем что 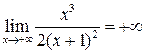
Поскольку
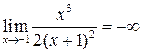 , то точка
, то точка 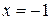 - точка разрыва второго рода, а
- точка разрыва второго рода, а 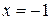 - вертикальная асимптота.
- вертикальная асимптота.
Найдём наклонные асимптоты 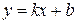 , где
, где
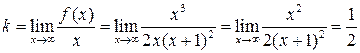
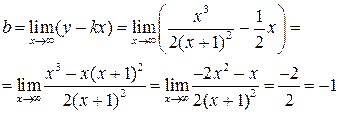
Следовательно, 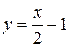 - уравнение наклонной асимптоты
- уравнение наклонной асимптоты
4. Производная
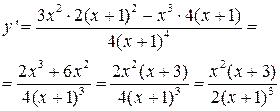 определена на
определена на 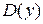
Поскольку 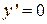 при
при 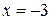 ,
, 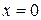 , то это критические точки функции. Так как
, то это критические точки функции. Так как
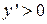 при
при 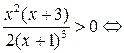
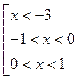
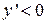 при
при 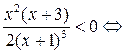
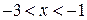
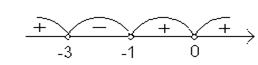 |
то на интервалах 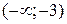 ,
, 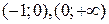 функция возрастает, а на интервале
функция возрастает, а на интервале
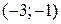 - убывает.
- убывает.
При 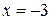 функция имеет максимум, т.к. переходе через эту точку
функция имеет максимум, т.к. переходе через эту точку 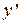 меняет знак с «+» на «
меняет знак с «+» на « 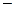 ».
».
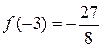 , значит точка
, значит точка 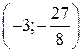 - точка максимума.
- точка максимума.
5. Находим вторую производную
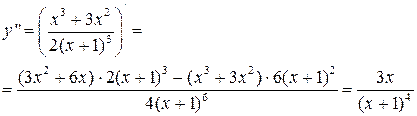
Она определена для 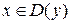 . Поскольку
. Поскольку 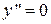 при
при 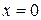 , то определив знак
, то определив знак 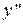 на каждом из интервалов
на каждом из интервалов 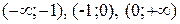 , получим, что для
, получим, что для 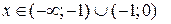
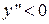 , график выпуклый; для
, график выпуклый; для 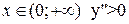 график вогнутый.
график вогнутый.
При переходе через точку 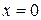 производная
производная 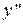 меняет знак, поэтому
меняет знак, поэтому 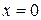 - точка перегиба, причём
- точка перегиба, причём 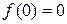 .
.
6. График функции пересекает координатные оси в т. 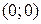 .
.
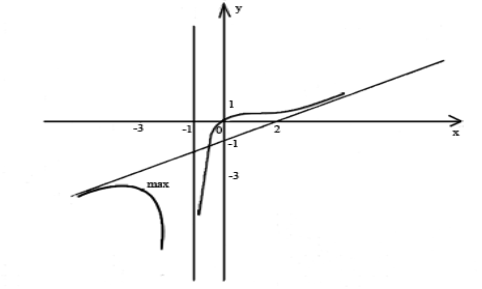
Задача 16.По формуле Тейлора с остаточным членом в форме Лагранжа у функции 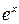 вычислить значение с точностью до
вычислить значение с точностью до 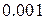 при
при 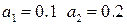 .
.
Решение:Формула Тейлора с остаточным членом в форме Лагранжа имеет вид
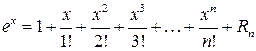
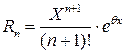 отсюда получаем
отсюда получаем 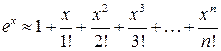
Для любого значения 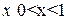 имеем
имеем 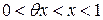 отсюда
отсюда 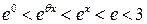 или
или 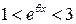 следовательно
следовательно 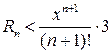 следованием
следованием 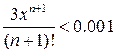 или
или 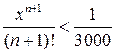
Следовательно, для заданной точности каждый отброшенный член должен быть меньше 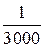 .
.
При 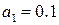 эта точность достигается при
эта точность достигается при 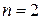 , а при
, а при 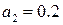
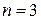 .
.
Ответ: 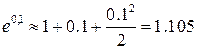
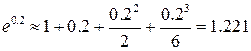 .
.
Задача 17.Найти наибольшее и наименьшее значения функции на отрезке 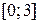
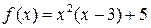
Решение: Функция определена на 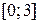
Производная 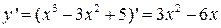 определена на
определена на 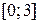 и обращается в нуль при
и обращается в нуль при 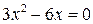
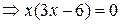
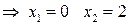 . Эти точки принадлежат отрезку
. Эти точки принадлежат отрезку 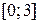 .
.
Тогда
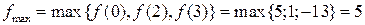
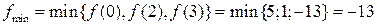
Ответ: 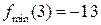 ,
, 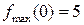 .
.
Задача 18.Разложить число 100 на два слагаемых так, чтобы их произведение было наибольшим.
Решение.Пусть 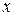 - первое слагаемое,
- первое слагаемое, 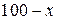 будет второе слагаемое.
будет второе слагаемое.
Произведение этих слагаемых даёт функцию 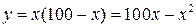 .
.
По условию задачи 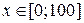 . Найдём экстремумы этой функции
. Найдём экстремумы этой функции 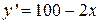 ,
, 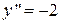 ,
,
то при 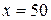 функция достигает максимума.
функция достигает максимума.
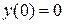
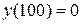 следовательно функция принимает наибольшее значение в критической точке
следовательно функция принимает наибольшее значение в критической точке 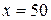 .
.
Ответ: Произведение двух слагаемых будет наибольшее, если они равны 50. 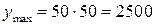
Задача 19.Отделить действительные корни уравнения
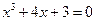
Применяя комбинированный метод вычислить их с точностью до шести десятичных знаков.
Решение: 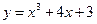 -непрерывная функция на всей области определения
-непрерывная функция на всей области определения 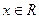 в точке x=0
в точке x=0 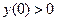 , а в точке x=-1 y(-1)=-4. Следовательно на отрезке [-1;0] функция
, а в точке x=-1 y(-1)=-4. Следовательно на отрезке [-1;0] функция 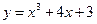 обращается в ноль и уравнение
обращается в ноль и уравнение 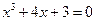 на этом отрезке имеет корень. Найдем
на этом отрезке имеет корень. Найдем 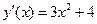 . Так как
. Так как 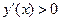 для всех
для всех 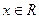 , то функция y(x) монотонно возрастает на всей области определения и имеет только единственный корень на отрезке [-1;0]. Уточним отрезок на котором находится корень. Разделим отрезок [-1;0] на десять частей и убедимся, что функция y(x) меняет знак только на отрезке [-0.7;-0.6]. Следовательно корень уравнения лежит на отрезке [-0.7;-0.6]. Заметим что чем точнее отделен корень, тем меньше шагов методом хорд и методом касательных надо выполнить. Проверим, для какой из этих двух точек выполняется условие
, то функция y(x) монотонно возрастает на всей области определения и имеет только единственный корень на отрезке [-1;0]. Уточним отрезок на котором находится корень. Разделим отрезок [-1;0] на десять частей и убедимся, что функция y(x) меняет знак только на отрезке [-0.7;-0.6]. Следовательно корень уравнения лежит на отрезке [-0.7;-0.6]. Заметим что чем точнее отделен корень, тем меньше шагов методом хорд и методом касательных надо выполнить. Проверим, для какой из этих двух точек выполняется условие 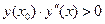 поскольку
поскольку 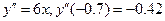 ,
, 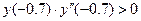 то применяя метод Ньютона положим
то применяя метод Ньютона положим 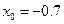 . Находим
. Находим 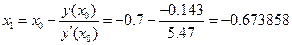 .
.
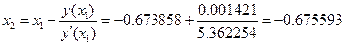 .
.
По методу хорд положим 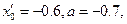 получим
получим 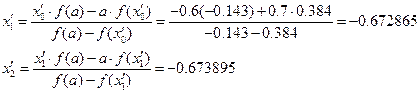
Следовательно корень данного уравнения находится на отрезке [-0.673593;-0.673585]. Данной точности еще недостаточно. Положим теперь a=-0,673593, найдем 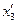 .
. 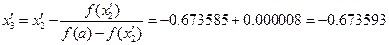 .
.
Таким образам x=-0.673593 корень данного уравнения. Заметим, чем точнее отделен корень первоначально, тем меньше шагов методом хорд и касательных надо выполнить.
Задачи для контрольной работы.
Задача 1.Вычислить определитель:
а) 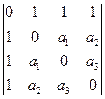 б)
б) 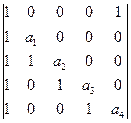
Значения 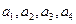 взять из таблицы 1.
взять из таблицы 1.
Задача 2.Найдите сумму 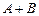 , разность
, разность 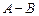 , произведения
, произведения 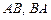 матриц
матриц 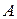 и
и 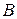 , если это возможно
, если это возможно
1. 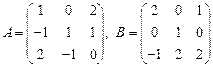 ; 2.
; 2. 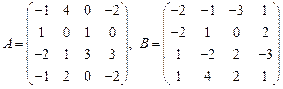 ;
;
3. 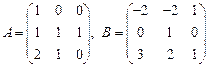 ;
;
4. 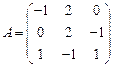 ,
, 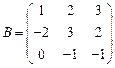 ;
;
5. 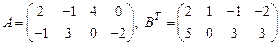 ; 6.
; 6. 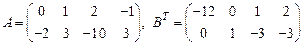 .
.
7. 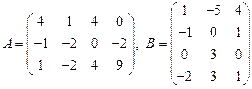 ;
;
8. 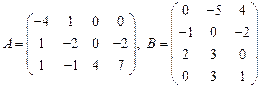 ;
;
9. 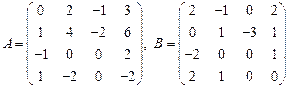 ;
;
10. 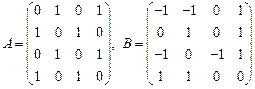 ;
;
11. 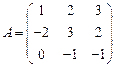 ,
, 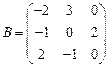
12. 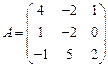 ,
, 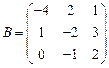 ;
;
13. 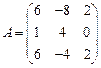 ,
, 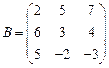 ;
;
14. 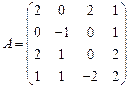 ,
, 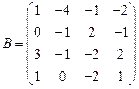 ;
;
15. 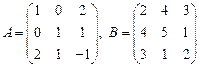 ;
;
16. 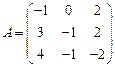 ,
, 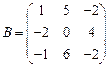 ;
;
17. 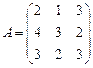 ,
, 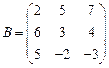 ;
;
18. 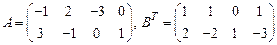 ;
;
19. 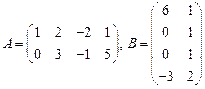 ; 20.
; 20. 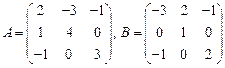 ;
;
21. 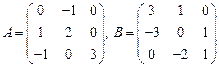 ; 22.
; 22. 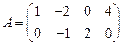 ,
, 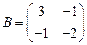 ;
;
23. 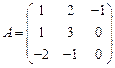 ,
, 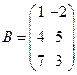 ;
;
24. 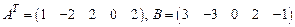 ;
;
25. 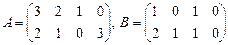 ;
;
26. 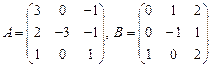 ;
;
27. 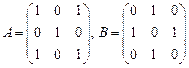 ;
;
28. 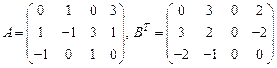 ;
;
29. 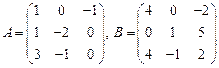 ;
;
30. 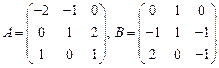 ;
;
31. 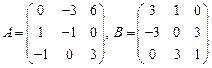 ;
;
32. 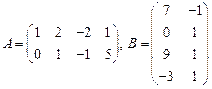 ;
;
33. 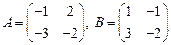 ;
;
34. 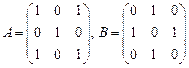 ;
;
35. 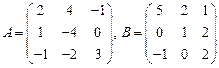 ;
;
36. 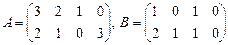 ;
;
37. 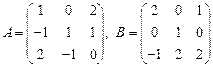 ; 38.
; 38. 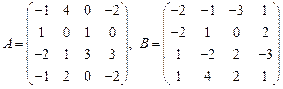 ;
;
39. 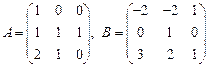 ;
;
40. 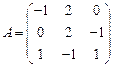 ,
, 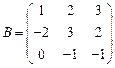 ;
;
41. 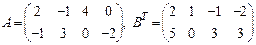 ;
;
42. 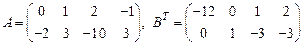 .
.
43. 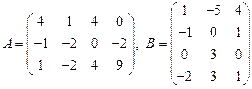 ;
;
44. 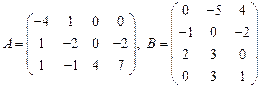 ;
;
45. 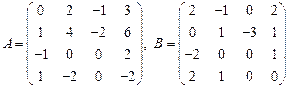 ;
;
46. 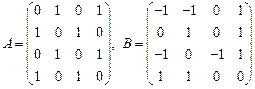 ;
;
47. 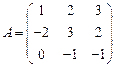 ,
, 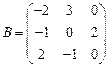
48. 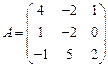 ,
, 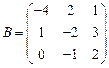 ;
;
49. 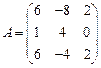 ,
, 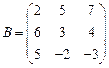 ;
;
50. 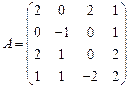 ,
, 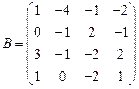 ;
;
51. 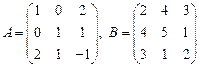 ;
;
52. 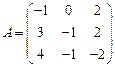 ,
, 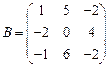 ;
;
53. 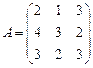 ,
, 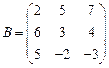 ;
;
54. 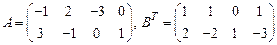 ;
;
55. 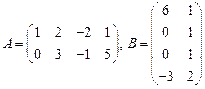 ; 56.
; 56. 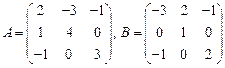 ;
;
57. 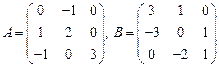 ; 58.
; 58. 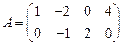 ,
, 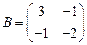 ;
;
59. 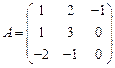 ,
, 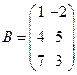 ;
;
60. 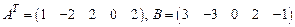 ;
;
61. 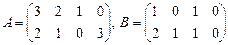 ;
;
62. 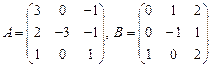 ;
;
63. 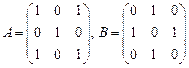 ;
;
64. 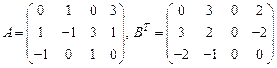 ;
;
65. 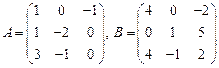 ;
;
66. 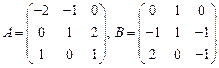 ;
;
67. 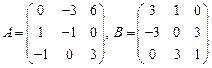 ;
;
68. 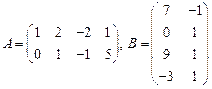 ;
;
69. 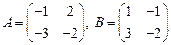 ;
;
70. 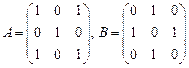 ;
;
71. 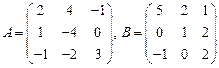 ;
;
72. 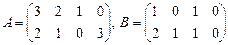 ;
;
73. 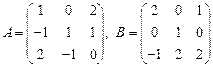 ; 74.
; 74. 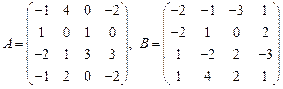 ;
;
75. 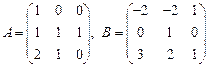 ;
;
76. 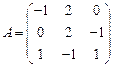 ,
, 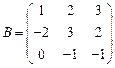 ;
;
77. 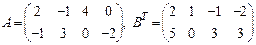 ; 78.
; 78. 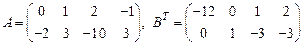 .
.
79. 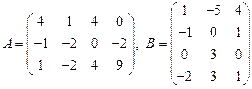 ;
;
80. 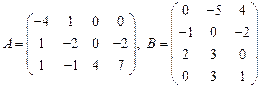 ;
;
81. 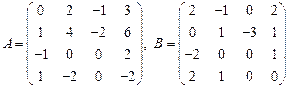 ;
;
82. 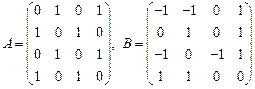 ;
;
83. 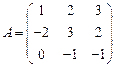 ,
, 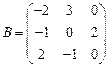
84. 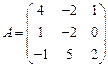 ,
, 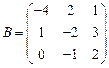 ;
;
85. 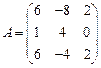 ,
, 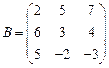 ;
;
86. 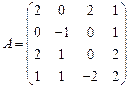 ,
, 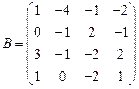 ;
;
87. 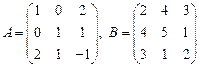 ;
;
88. 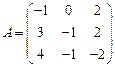 ,
, 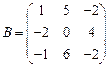 ;
;
89. 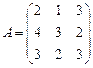 ,
, 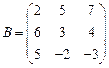 ;
;
90. 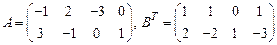 ;
;
91. 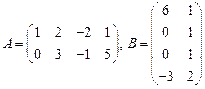 ; 92.
; 92. 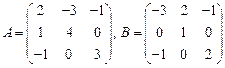 ;
;
93. 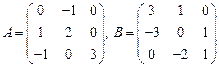 ; 94.
; 94. 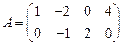 ,
, 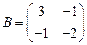 ;
;
95. 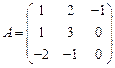 ,
, 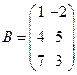 ;
;
96. 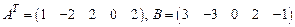 ;
;
97. 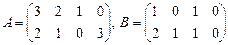 ;
;
98. 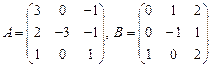 ;
;
99. 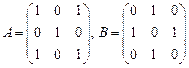 ;
;
100. 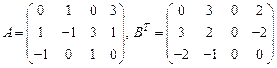 .
.
Задача 3.Даны векторы 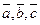 . Проверить, что векторы
. Проверить, что векторы 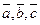 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 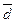 в этом базисе. Вычислить скалярное и векторное произведение векторов
в этом базисе. Вычислить скалярное и векторное произведение векторов 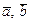 .
.
