Элементарные функции. Классификация функций

Говорят, что функция задана явно, если она задана формулой, в которой правая частьне содержит зависимой переменной; например, функция .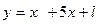

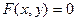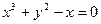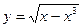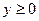Напротив, функция задана неявно, если она задана уравнением , не разрешенным относительно зависимой переменной. Например, функция, заданная уравнением , задана неявно. (Заметим, что последнее уравнение задает две функции, при , и 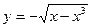при y<0).

Обратная функция.

Пусть 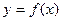есть функция независимой переменной 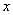, определенной на промежутке 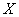с областью значений 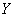. Поставим в соответствие каждому 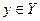единственное значение 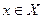, при котором 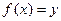. Тогда полученная функция 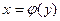, определенная на промежутке 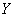с областью значений 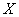, называется обратной функцией и обозначается 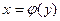или .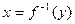

Например. Для функции 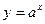обратной будет функция .

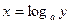Можно доказать, что для любой строго монотонной функции 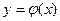существует обратная функция.

Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.

Сложная функция.

Пусть функция 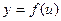есть функция от переменной u, определенной на множестве U с областью значений Y,а переменная u в свою очередь является функцией 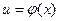от переменной x, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция 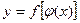называется сложной функцией.

Определение

Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Например, функция

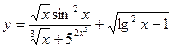
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции ( 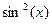, , 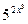, 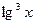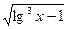) конечно. Примерами неэлементарных функций являются функции 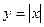, 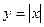– целая часть числа x.

Классификация функций.

Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).

Определение

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.

К числу алгебраических функций относятся:

- целая рациональная функция (многочлен или полином): ;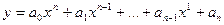

- дробно–рациональная функция – отношение двух многочленов;

- иррациональная функция (если в составе операций над аргументом имеется извлечение корня).

Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.

Преобразование графиков.

Пусть задан график функции 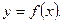. Тогда справедливы следующие утверждения.

1. График функции 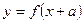есть график 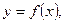, сдвинутый (при a>0 влево, при a<0 вправо) на |a| единиц параллельно оси 0x.

2. График функции 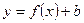есть график 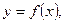, сдвинутый (при b>0 вверх, при b<0 вниз) на |b| единиц параллельно оси 0y.

3. График функции 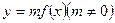есть график 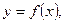, растянутый (при m>1) в m раз или сжатый (при 0<m<1) вдоль оси 0y. При 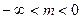график функции 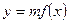есть зеркальное отображение графика 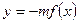от оси 0x.

4. График функции 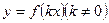есть график 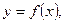, сжатый (при k>1) в k раз или растянутый (при 0<k<1) вдоль оси 0x. При 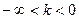график функции 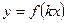есть зеркальное отображение графика 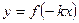от оси 0y.