Система нелінійних рівнянь

Коротко розглянемо кожний з методів.

I. Метод дихотомії.

Припустимо, що 1-ша частина задачі вирішена, тобто знайшли [a,b]. Нехай на [a,b] неперервна функція f(x) має лише один корінь (f(a)f(b)£0). Нехай для визначеності f(a)>0, f(b)<0. Обираємо точку x₀=(a+b)/2. Підраховуємо f(x₀). Якщо f(x₀)>0, то корінь р-ня лежить на відрізку (x₀,b). Якщо f(x₀)<0, то корінь лежить на відрізку (a, 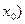. Далі, двох інтервалів (a, 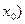, (x₀,b) обираємо той, на границях якого функція має різні знаки, знаходимо точку 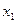– середину вибраного інтервалу, обчислюємо 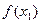і повторюємо вказаний процес.

В результаті отримаємо послідовність інтервалів, що містять шуканий

корінь 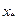, при чому довжина кожного наступного інтервалу буде в два рази менша за попередній. Процес закінчується, коли довжина отриманого інтервалу менша числа 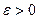, в якості кореня 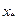наближено приймається середина цього інтервалу. Якщо на (a,b) є декілька коренів, то вказаний процес зійдеться до одного з них.

Переваги. 1) простота; 2)цей метод відноситься до глобально-збіжних методів (обов’язково знайдемо корінь).

Недоліки. 1) збіжність повільна; 2) метод не можна узагальнити для розв’язання системи рівнянь.

II. Метод простої ітерації (умовно-збіжний метод).

Рівняння (1) замінюється еквівалентним рівнянням x=g(x) (2). Ітерації здійснюються за правилом x_k+1=g(x_k), k=0,1,... (для систем 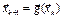) (3), x₀ - відоме початкове наближення. Для збіжності велике значення має вибір функції g(x) .

Озн. Функція g(x) називається Ліпшиць-неперервною зі сталою a на множині X, якщо " x₁, x₂ Î X виконується нерівність 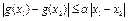(4).

Теорема. Якщо на 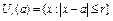функція g(x) Ліпшиць-неперервна зі сталою a Î (0,1) і виконується умова 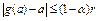, то ітераційний процес (3) веде до єдиного розв’язку рівняння (2) при " x₀ Î U_r(a). Для похибки роз-ку справедлива нерівність: .

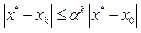Теорема показує умовний характер збіжності. Метод простої ітерації має лінійну збіжність.

Наслідок. Умова (4) на неперервн-диф. функції g(x) еквівалентна умові: 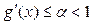. (1) перетворюється в (2) так, щоб умова збіжності виконувалася: х = x + t(x)f(x), де t - неперервна і знакостала функція на проміжку наближень..

III Метод релаксації.

Коли t(x)= t=const, отримаємо ітераційний процес: 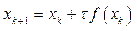і для якого 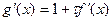і метод збіжний при умові (*).

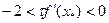Припустимо, що 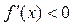, 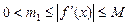₁ (5) , де М₁ – максимум першої похідної, m₁– мінімум. Щоб виконувалась умова (*) t повинно задовольняти: 0 < t £ М₁ . Якщо t задовольняє цю умову, то процес збіжний. Підберемо t так, щоб процес (3) збігався якнайшвидше:

x_k- 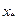=z_k, z_k=x_k- 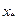– підставляємо в рівняння релаксації і отримаємо 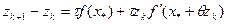, 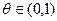. (розклад в ряд Тейлора). Можна записати 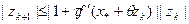, Якщо виконується умова (5), то одержимо 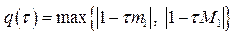. Потрібно мінімізувати 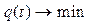і тоді отримаємо .

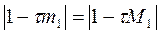IV Метод Ньютона.

Нехай f(x)=0 – двічі неперервно-диференційовна функція, тоді можна записати: .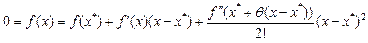

Звідси отримаємо .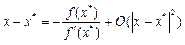

Отже, отримали ітераційний процес 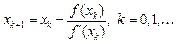– формула Ньютона. (Для системи рівнянь - 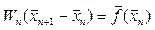, де W - матриця Якобі). Обчислення рішення рівняння за допомогою такого ітераційного процесу називається методом Ньютона.

На відміну від МПІ у цьому методі похибка на наступному кроці буде вести себе як квадрат похибки у попередньому кроці.

Основні недоліки методу Ньютона:

1. Умови збіжності в методі значно жорсткіші і для багатьох випадків їх фактично не можливо одержати.

2. На кожному кроці треба підраховувати похибку.

x₀ шукають іншими методами (наприклад, метод дихотомії: 1) метод Ньютона; 2) якщо 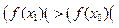, тоді відрізок [x₀, x₁] ділиться навпіл і йде метод дихотомії; 3) знов далі метод Ньютона.)

Система нелінійних рівнянь

Розглянемо сис-му нелін. рівнянь:

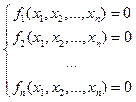, у векторній формі 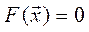(6)

f_i – функції дійсних змінних. Методи розв’язування є ітераційними (щоб його запустити потрібно мати наближення). В загальному випадку дослідити (6) на наявність і кількість розв’язків досить вожко.

Знаходити розв’язок сис-ми нелін. рівнянь можна з допомогою таких методів:

Лінійні:

1. Метод простої ітерації (МПІ).

2. Метод релаксації.

3. Метод Пікара.

4. Метод Ньютона.

Нелінійні:

5. Метод Якобі.

6. Метод Зейделя.

Вище ми вже розглянули МПІ, Метод релаксації та метод Ньютона. Отже, далі опишемо тільки методи Пікара, Якобі і Зейделя.

Метод Пікара.

Будемо вважати, що розв’язок x* існує. В багатьох випадках функція 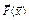має такий вигляд: 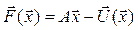, де A - невироджена матриця, 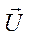- вектор функція. Наше рівняння приймає вигляд 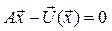. Будуємо ітераційний процес за схемою 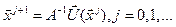- це метод Пікара. Вважається, що лінійна частина рівняння міститься в матриці A.

Недолік: треба обчислювати обернену матрицю для A. Тому можна робити так: 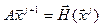. Але тоді на кожному кроці треба розглядати систему лінійних алгебраїчних рівнянь.

В загальному випадку метод записується у вигляді 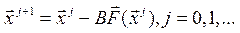(7), де B - деяка не вироджена матриця.

Всі розглянуті вище методи були лінійними, тепер розглянемо декілька нелінійних методів.

Метод Якобі.

Якщо є сис-ма (6) , то можемо розглянути метод Якобі:

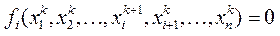, Метод Якобі реалізується: маємо наближення, замінимо:

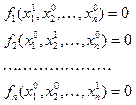Одержали сис-му з n нелінійних рівнянь. Ця сис-ма розпадається на n окремих нелін. рівнянь. Для розв’язку 2-го р-ня використаємо роз-к 1-го рі-ня, для ро-ку останнього: 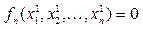. Це багатокроковий метод, так як знаходження роз-ку в останній точці використовується інформація в декількох попередніх точках. Щоб прискорити цей метод використовують метод Зейделя.

Метод Зейделя

Нехай задана система лінійних рівнянь, 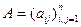(*) , де в матриці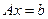

всі діагональні не дорівнюють нулю. Якщо і-те рівняння системи (*) поділити на 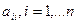, а потім всі невідомі, крім 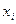, перенести вправо, то ми прийдемо да еквівалентної системи 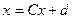, де , , ,

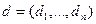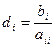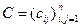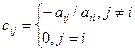
Метод полягає в тому, що ітерації проводяться по формулі: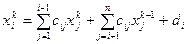

де 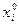– довільні, і=1,2,...,n; k=1,2,…

Теорема Для існування єдиного розвязку системи (*) і збіжності методу Зейделя достатньо виконання однієї з умов

1)

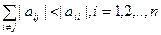
2) Матриця А– симетрична додатньо визначена (всі її власні числа додатні).

2. Чисельні методи розв’язання систем лінійних рівнянь. Числа обумовленості СЛР.

Розглянемо чисельні методи розв’язання систем лінійних алгебраїчних рівнянь

Ax=f (1)

де A - матриця n*n, має обернену. x = ( 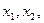, ... , 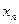) 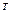- шуканийвектор,

f =( 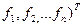-заданий вектор.

Припускаємо, що визначник матриці А відмінний від нуля, так що існує єдиний розв’язок х. Розрізняють прямі та ітераційні методи роз-ня СЛР. У прямих (або точних) методах розв’язок x системи (1) відшукується за скінчену кількість арифметичних дій. Внаслідок похибок заокруглення прямі методи насправді не приводять до точного розв’язку системи (1) і назвати їх точними можливо лише залишаючи осторонь похибки заокруглення. Ітераційні методи (їх також називають методами послідовних наближень) полягають у тому, що розв’язок x системи (1) відшукується як границя при 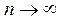послідовних наближень 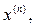де n- номер ітерації. Як правило, за скінчену кількість ітерацій ця границя не досягається. Як правило число 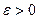(точність) задається і обчислення проводяться до тих пір, поки не виконується умова .

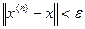Прямі методи

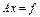перетворюється в 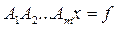, де A_i - матриці n´n такі, що системи з такими матрицями розв’язуються легко. Позначимо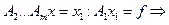 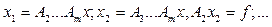. Тепер опишемо матриці, з якими легко працювати:

P - матриці, отримані перестановкою рядків чи стовпчиків в одиничній матриці E. P - ортогональні P^-1=P^T, PM - перестановка рядків, NP - перестановка стовпчиків. 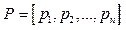, p_i - на якому місці в i-му рядку стоїть 1

ортогональні матриці: Q^-1=Q^T, 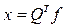- розв’язок

діагональні матриці

блоково - діагональні матриці, на діагоналі Жорданові клітини розміру 1 чи 2

нижні діагональні матриці (вище діагоналі - 0)

верхні трикутні матриці