Вектор-функция, ее предел и непрерывность

Глава 3. ВЕКТОРНЫЕ ФУНКЦИИ

Пусть Х и Y – два множества, f – отображение Х в Y, т.е. некоторое правило, в силу которого каждому элементу в множестве Y соответствует единственный элемент y = . Элементы множеств Х и Y могут быть любыми математическими обьектами: числами (вещественными или комплексными), векторами, матрицами и т.п. Иногда термину “отображение” предпочитают термин “функция”. В частности, если Х представляет собой некоторое числовое множество, отображение чаще на- зывают функцией аргумента х , . Если при этом элементы множества Y также яв-ляются числами, f называют числовой или скалярной функцией; о таких функциях шла речь в предыдущих параграфах. Если же множество Y состоит из векторов, отоб- ражение называют векторной функцией или, короче, вектор-функцией.

Математическое понятие вектор-функции можно иллюстрировать разнообраз- ными примерами векторных величин, вэятыми из механики, физики и других естест- венных наук. Так, хаотичное броуновское движение малой частицы вызвано тем, что вектор действующей на неё силы (равнодействующей столкновений частицы с молеку- лами жидкости или газа) ежемоментно меняется и по направлению, и по величине. Эту силу можно рассматривать как вектор-функцию, аргументом которой является время.

В этом параграфе изложены основы дифференциального исчисления вектор-функций.

Вектор-функция, ее предел и непрерывность

1.1. Основные понятия

Пусть Т – некоторое множество вещественных чисел, и пусть на Т определена вектор-функция (t), т.е. сформулировано некоторое правило, согласно которому каж-дому Т соответствует единственный вектор 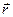= 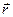(t).. Обозначим через x(t), y(t) и z(t) проекции вектора (t) на координатные оси соответственно абсцисс, ординат и ап- пликат декартовой прямоугольной системы координат. Очевидно, x(t), y(t) и z(t) – ска- лярные функции, определенные на множестве Т , причём на Т справедливо разложе- ние вектора (t) по базису, составленному из ортов координатных осей:

= (x(t), y(t), z(t) ).

Функции x(t), y(t) и z(t) называют координатными функциями вектор-функции (t). Следовательно, если на множестве Т определена вектор-функция (t), то на Т определена и упорядоченная тройка (x(t), y(t), z(t) ) её координатных (скалярных) функ- ций.

Заметим, что справедливо и обратное: если (x(t), y(t), z(t) ) - упорядоченная тройка каких-то скалярных функций, определенных на Т, то на Т можно определить вектор-функцию (t) с помощью равенства: . Таким образом, задание на каком-либо множествевектор-функции эквивалентно заданию на этом множестве упорядоченной тройки скалярных функций.

Может оказаться, что все значения (t), , компланарны, т.е. параллельны некоторой плоскости. Введя на этой плоскости декартову прямоугольную систему координат, получим: , где и 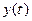– проекции вектора (t) на оси Ox и Oy соответственно. Таким образом, в этом случае задание на множестве T, , вектор- функции (t) эквивалентно заданию на T упорядоченной пары скаляр- ных функций: . Можно, конечно, и здесь считать, что на T задана упорядоченная тройка функций , причем 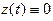на T. Везде ниже мы связываем задание вектор- функции с заданием упорядоченной тройки скалярных функций.

Удобной геометрической интерпретацией вектор- функции является её годограф.По- местим начало вектора (t) в начало координат и обозначим его конец через За- метим, что координатные функции образуют набор координат этой точки: (x(t), y(t), z(t)). Когда t, возрастая, пробегает множество T, точка перемещается, описывая некоторую кривую Г (см. рис. 1). Эту кривую и называют годографом вектор- функции (t). Переменную t называют параметром кривой Г, уравнения x = x(t), y = y(t), z = z(t) – параметрическими уравнениями кривой Г Систему

будем называть координатной формой уравнения кривой Г, а эквивалентное этой сис- теме векторное уравнение , Т , где , - векторной формой уравнения этой кривой.

Пример 1. Пусть = и 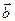= , – заданные векторы. Отложим 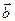из начала координат O и обозначим через D прямую, проходящую через конец вектора 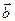, точку В параллельно . При всяком вещественном t поло- жим: . Прямая D является годографом. этой вектор- функции, а система

- координатной формой уравнения прямой.

1.2. Предел вектор- функции в точке

Пусть t₀ – вещественное число, а - вектор- функция определенная в проко- лотой окрестности Пусть, далее, - некоторый вектор.

Определение.Вектор называют пределом вектор-функции при t, стремя- щемся к t₀ , если для любого ε> 0 можно указать δ>0 такое, что при всех t, принадлежа- щих проколотой δ – окрестности точки t₀ , длина разности векторов и меньше ε. .

Если удовлетворяет условиям этого определения, будем записывать: = ( является пределом при t, стремящемся к t₀ ) или ( стремится к при t, стремящемся к t₀ ).

Итак, равенство по определению означает:

,

где |t- t₀ | есть модуль разности двух чисел, а | - | - длина разности двух векторов ( см. рис. 2)

Замечание. Обозначим: φ(t) = . Очевидно, φ(t) - скалярная функция, определённая в проколотой окрестности , причём ( см. выше)

, т.е., ( см. определение предела скалярной функции на языке «ε-δ»). Таким образом, тогда и только тогда, когда длина разности - является бесконечно малой при t t₀ :

. (1)

Теорема 1 устанавливает связь между пределом вектор-функции и пределами её координатных функций

Теорема 1.(О покоординатной сходимости) Пусть вектор-функция опре- делена в проколотой окрестности точки t₀ , t₀ 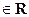, а x(t), y(t) и z(t) - её координат- ные функции. Пусть, далее, - некоторый вектор, а , его координаты. Вектор является пределом вектор-функции при 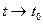тогда и только тогда, когда его координаты являются пределами при 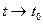соответствующих координатных функций:

►Имеем: =( ) и . Отсюда:

. Подкоренное выражение представляет собой сумму трёх неотрицательных слагаемых; поэтому левая часть этого равенства стремится к нулю при 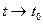тогда и только тогда, когда каждое из этих слагаемых стремится к нулю при 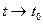, т.е.

( ) , что можно переписать так:

( ) (2) Утверждение теоремы следует из (1) и (2). ◄

Следствие.Если = , то =| |. ► = = = | | . ◄

Замечание. Если =| |, то вовсе не обязательно справедливо равенство = . Вместе с тем, справедливо утверждение:

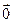
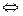
= = 0

- это вытекает из (1) как частный случай при = .

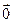Опираясь на теорему о покоординатной сходимости можно доказывать теоремы о пределах вектор-функций, аналогичные теоремам о пределах скалярных функций.

Теорема 2.(О единственности предела) Если вектор-функция имеет пре- дел при 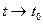, то только один.

► Допустим, что вектор-функция имеет при при 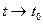два различных предела: =( ) и =( ). Так как ≠ , то упорядо- ченные тройки их координат не могут совпадать. Пусть, к примеру, ≠ . В силу тео- ремы о покоординатной сходимости координатная функция x(t) должна при 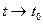стремиться и к , и к ; но это противоречит теореме о единственности предела ска- лярной функции. ◄

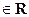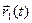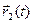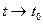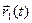
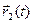
Теорема 3.(О действиях над пределами вектор-функций) Пусть в проколотой окрестности точки t₀ , t₀ , определены вектор-функции и и скалярная функция λ(t), и пусть эти функции имеют пределы при : , λ(t) λ . Тогда:

1) ; 2) ;

3) ; 4) .

► Доказательства всех четырёх утверждений проводятся по единой схеме, по- этому достаточно продемонстрировать одно из них . Изложим доказательство утверж- дения 4).

Запишем разложения векторов 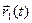, , 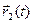и по базису , составлено- му из ортов координатных осей:

, ,

, . Используя формулу векторной алгебры, запишем разложение вектора векторного про- изведения :

= =

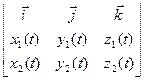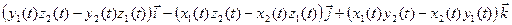= Из теоремы об арифметических действиях с пределами скалярных функций и теоремы о покоординатной сходимости следует:

;

;

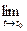
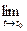
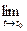
. Опираясь на эти равенства и теорему о покоординатной сходимости, теперь получим:

= = . ◄

Замечание. Для векторов не определены отношения «больше» или «меньше»; утверждение « вектор больше вектора » смысла не имеет. По этой причине среди теорем о вектор-функциях нет аналогов тех теорем о пределах скалярных функций, формулировки которых содержат неравенства, а именно, теоремы о предельном пере- ходе в неравенстве, о стабилизации знака неравенства, о «сжатой» функции.

Пусть вектор-функция определена на интервале (α,β) , а - некоторый вектор.

Определение. Вектор назовём односторонним пределом вектор-функции при t, стремящемся к α справа (при t, стремящемся к β слева ), если для любого ε> 0 можно указать δ>0 такое, что при всех t, принадлежащих интервалу (α, α + δ) при- надлежащих интервалу ( ) , длина разности - меньше ε.

Пусть вектор-функция определена на интервале (α,β) , а x(t), y(t) и z(t) - её координатные функции. Пусть, далее, - некоторый вектор, а , его координаты. Справедливы утверждения, аналогичные теореме о покоорди- натной сходимости:

;

.

Доказательства этих утверждений нетрудно скопировать с доказательства тео- ремы о покоординатной сходимости .

Теорема 4. (О связи предела вектор-функции с её односторонними пределами)

Пусть вектор-функция определена в проколотой окрестности точки t₀ , t_{0 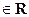,}, а - некоторый вектор. Для того, чтобы являлся пределом при 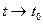, необходимо и достаточно, чтобы этот вектор был односторонним пределом и при t, стремящемся к t₀ слева, и при t, стремящемся к t₀ справа:

( = ) ( = = ) .

►Пусть x(t), y(t) и z(t) - координатные функции вектор-функция , а , -координаты вектора .

Необходимость. Пусть = . По теореме о покоординатной сходимости , , . Отсюда по теореме об односторонних пределах скалярной функции следует: , , .Отсюда и из сформулированных выше аналогов теоремы о покоординатной сходимости следует: = .

Доказывая Достаточность следует приведенные выше рассуждения располо- жить в обратном порядке. ◄

1.3. Непрерывность вектор- функции

Определение. Вектор-функцию называют непрерывной в точке t₀ , t₀ 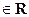, если она определена в некоторой окрестности этой точки, а её предел при 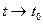равен .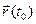

Теорема 5.(Критерий непрерывности) Пусть вектор-функция определена в окрестности . t₀ 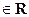. Для того, чтобы была непрерывной в точке t₀, необхо- димо и достаточно, чтобы каждая из её координатных функций была непрерывной в этой точке.

► Пусть x(t), y(t) и z(t) - координатные функции вектор-функции : Обозначим: х₀ = х(t₀), у₀ = y(t₀), z_{0 =} z(t₀) ; тогда . В силу теоремы о покоординатной сходимости

. Отсюда вытекает справедливость утверждений теоремы, так как равенство в левой части есть условие непрерывности вектор-функции в точке t₀, а равенства в правой части – условия непрерывности её координатных функций в той же точке. ◄

Разность t – t­₀ будем называть приращением аргумента t в точке t₀ и обозначать через Δt или h. Заметим: t = t­₀ + Δt= t­₀ + h. Вектор разности - 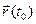= - 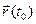= 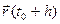- 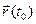назовем приращением вектор-функции в точке t₀ и обозначим че- рез Δ 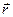или через Δ 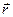(h), подчеркнув во втором обозначении зависимость этого векто- ра от приращения h = Δt аргумента t. Заметим: .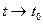

Теорема 6 (О приращении непрерывной вектор-функции) Пусть вектор-функция определена в окрестности . t₀ 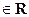. Для того, чтобы была непрерывной в точке t₀, необходимо и достаточно, чтобы её приращение было бесконечно малым при : .

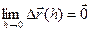►Пусть 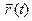, х₀ = х(t₀), у₀ = y(t₀), z₀ = z(t₀) ; тогда - 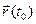= (x(t)- x(t₀), y(t)- y(t₀), z(t) - z(t₀)), т.е.

Δ 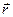(h) = 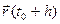- 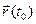= (x(t₀+h )- x(t₀), y(t₀+h )- y(t₀), z( t₀+h) - z(t₀)) =

= (

По теореме о покоординатной сходимости

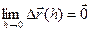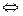( ) ( , , ). Отсюда и из теоремы 5 вытекает справедливость утверждений теоремы 6, так как по теореме о приращении непрерывной скалярной функции равенства , , представляют собой необходимые и достаточные условия непрерывности в точке t₀ соответствующих координатных функций ◄

Определение. Вектор-функцию назовем непрерывной на интервале (α,β) , если она непрерывна в каждой его точке. Вектор-функцию назовём непрерывной на сегменте [α,β] , если она непрерывна на интервале (α,β) и, кроме того, непрерывна в точке α справа ( т.е. ) и непрерывна в точке β слева ( т.е. ).