Пример выполнения типового расчета
| Условие типового расчета | |||||||||||||||||
| Вариант Уравнение | Матрица A | Матрица B | |||||||||||||||
| 930207 A * X = B |
|
|
Выполнение типового расчета
1. Найдем обратную матрицу A-1 по формуле (4)
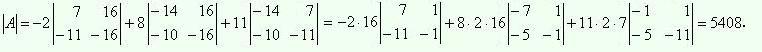
При вычислении определителя использовано разложение его по первой cтроке. Получившиеся определители второго порядка упрощены вынесением общего множителя из какой-либо строки или столбца. Затем найдем матрицу алгебраических дополнений:

 .
.
Тогда 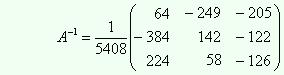
Для удобства дальнейших расчетов не будем умножать матрицу на множитель, стоящий перед ней.
Проведем контроль расчетов, для этого перемножим матрицы A и A-1. Если расчеты проведены верно, результатом должна быть единичная матрица.
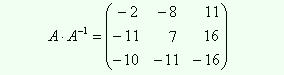 | 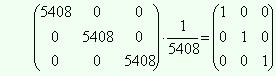 |
 |
При умножении использована удобная форма записи, при которой вторая матрица-сомножитель записывается правее и ниже первой, а правее первой и выше второй записывается результат умножения. При такой записи каждое число матрицы–результата стоит на пересечении той строки первой матрицы и того столбца второй матрицы, скалярное произведение которых дает искомое число.
3) Решение X уравнения A · X = B найдем по формуле (5).
X = B · A-1 = 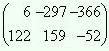 | 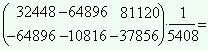  |
 |
X =  .
.
Теперь подставим матрицу X в исходное уравнение для проверки полученного результата:
X · A = B
X·A =  | 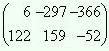 = B = B |
 |
Оформление отчета
В отчете по ТР должны быть представлены: расчет обратной матрицы A-1, проверка ее умножением матриц Aна A-1, расчет искомой матрицы X, проверка найденного результата подстановкой матрицы X в исходное уравнение.
В ответе необходимо записать определитель матрицы A и матрицу X :
|A| = 5408 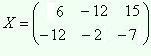 .
.
Решение систем линейных уравнений
Порядок выполнения работы:
В отчете по типовому расчету должны быть представлены преобразования расширенных матриц каждой системы. Полученные решения должны быть проверены умножением матрицы коэффициентов на матрицу решений.
В конце работы вписать общий ответ, в котором для каждой из систем указать:
- определитель матрицы коэффициентов;
- ранг матрицы коэффициентов и присоединенной матрицы;
- выводы сделанные на основании теоремы Кронекера-Капелли:
система является совместной или несовместной, если совместной, то определенной или неопределенной;
если система определенная, решение выписывается в виде столбца;
если система неопределенная, решение необходимо записать в векторном виде, выделяя фундаментальную систему решений однородной и частное решение неоднородной системы.
Литература
1. Высшая математика. Раздел: Линейная алгебра и аналитическая геометрия. Учебное пособие по выполнению типовых расчетов. М., МИСиС, 1990, N 687, стр.17-32.
