Метод розв`язання: ділення лівої та правої частини рівняння на або .
Приклад. Розв`язати рівняння :
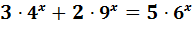
Розв`язання
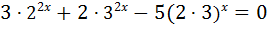
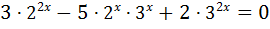 – однорідне показникове рівняння
– однорідне показникове рівняння
Поділимо обидві частини рівняння на 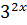 (
( 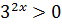 ).
).
Зверніть увагу! 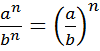 |
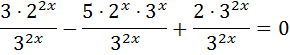
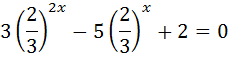
Зробимо заміну змінної 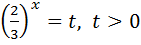 ,маємо:
,маємо:
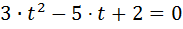
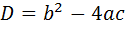
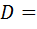 (
( 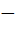 5)2
5)2 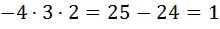 ;
; 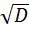 =1
=1
t1 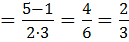
t2 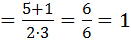
Повертаючись до заміни , маємо:
1) 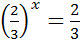 , звідси
, звідси 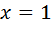 .
.
2) 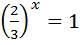
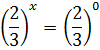
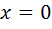 Відповідь: 0; 1.
Відповідь: 0; 1.
Вправи для самостійного розв’язування до теми 3:
1) 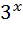 =
=  ; 16)
; 16) 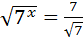 ;
;
2) 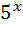 =
= 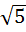 ; 17)
; 17) 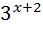 +
+ 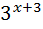 =108 ;
=108 ;
3) 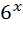 =
= 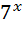 ; 18)
; 18) 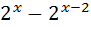 =24 ;
=24 ;
4) 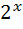 =
= 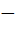 4 ; 19)
4 ; 19) 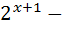 7
7 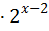 =16 ;
=16 ;
5) 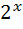 =16 ; 20)
=16 ; 20) 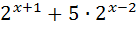 =104 ;
=104 ;
6) 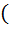 0,6
0,6 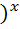 =
= 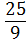 ; 21)
; 21) 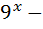 12
12 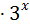 +27=0 ;
+27=0 ;
7) 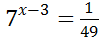 ; 22)
; 22) 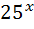 +4
+4 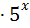 =5 ;
=5 ;
8) 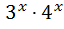 = 144 ; 23)
= 144 ; 23) 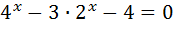 ;
;
9) 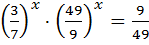 ; 24) 4
; 24) 4 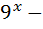 6
6 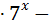 7=0 ;
7=0 ;
10) 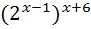 =1 ; 25)
=1 ; 25) 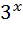 +5
+5 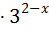 =14 ;
=14 ;
11) 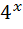 =8 ; 26)
=8 ; 26) 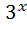 +
+ 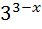 =12 ;
=12 ;
12) 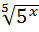 =25 ; 27)
=25 ; 27) 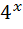 +1
+1  3
3 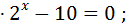
13) 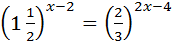 ; 28)
; 28) 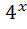 +3
+3 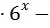 4
4 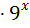 =0 ;
=0 ;
14) 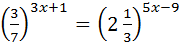 ; 29)
; 29) 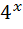 +2
+2  1
1 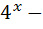 3
3 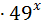 =0 ;
=0 ;
15) 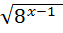 =
= 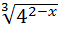 ; 30) 3
; 30) 3 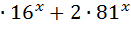 = 5
= 5 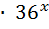 .
.
Тема 4 . Показникові нерівності.
1.Нерівність, яка містить змінну в показнику степеня, називають показниковою.
Розв`язання показникових нерівностей ґрунтується на властивостях показникової функції, а саме:
1)Функція 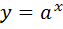 зростаєпри
зростаєпри 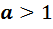 .
.
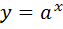 спадаєпри
спадаєпри 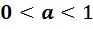 .
.При нерівність виду рівносильна
 нерівності
нерівності 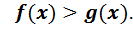
При нерівність виду рівносильна
Нерівності .
Розв`язання показникових нерівностей методом зведення обох частин до однієї основи.
Зверніть увагу! 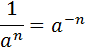 |
1)Розв’яжіть нерівність :
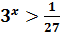
Зводимо до основи 3
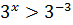
Оскільки 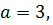 тобто
тобто 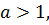 функція
функція 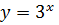 є зростаючою, тоді при порівнянні показників степеня знак нерівності не змінюється.
є зростаючою, тоді при порівнянні показників степеня знак нерівності не змінюється.
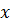 |
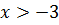
Відповідь: 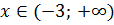
2) Розв’яжіть нерівність : 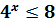
Зводимо до однієї основи 2, маємо: 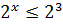
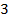 |
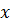 |
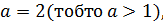 тоді при порівнянні показників степенів знак нерівності не змінюється.
тоді при порівнянні показників степенів знак нерівності не змінюється. Отже, 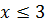
Відповідь: 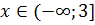
3) Розв’яжіть нерівність : 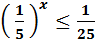
Зводимо до однієї основи 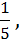 отримаємо:
отримаємо:
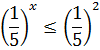
Оскільки 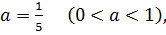 функція
функція 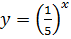 є спадною, тоді при порівнянні показників знак нерівності змінюється на протилежний.
є спадною, тоді при порівнянні показників знак нерівності змінюється на протилежний.
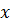 |
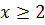
Зверніть увагу! 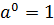 |
Відповідь: 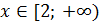
4)Розв’яжіть нерівність:
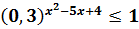
Запишемо праву частину нерівності у вигляді степеня з основою 0,3 , тобто 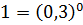
Маємо нерівність: 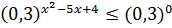
Оскільки 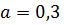
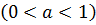 , тоді при порівнянні показників степенів знак нерівності змінюється на протилежний, тобто
, тоді при порівнянні показників степенів знак нерівності змінюється на протилежний, тобто
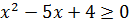
Зверніть увагу! 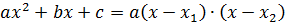 |
Для розв’язування одержаної квадратичної нерівності знайдемо корені квадратного рівняння 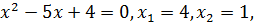 та розв’яжемо нерівність методом інтервалів:
та розв’яжемо нерівність методом інтервалів: 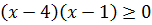
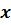 |
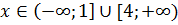
5)Розв’яжіть нерівність:
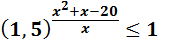
Запишемо праву частину нерівності у вигляді степеня з основою 1,5 , тобто:
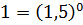
Оскільки 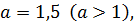 тоді при порівнянні показників степенів знак нерівності не змінюється, тобто:
тоді при порівнянні показників степенів знак нерівності не змінюється, тобто:
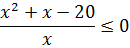
Розв’яжемо нерівність методом інтервалів,
ОДЗ: 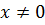
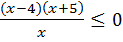
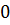 |
Відповідь: 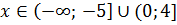
6)Розв’яжіть нерівність:
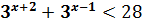
У лівій частині нерівності винесемо за дужки степінь з найменшим показником 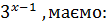
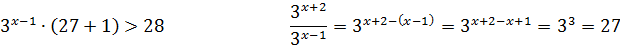
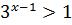
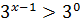
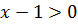
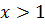
Відповідь: 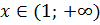
7) Розв’яжіть нерівність: 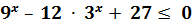
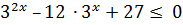
Зробимо заміну змінної 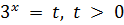
Маємо: 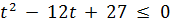
Розв’яжемо нерівність методом інтервалів. Для цього знайдемо корені квадратного рівняння.
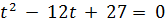
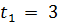
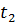
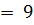
(t – 3) (t – 9) ≤ 0
+ − +
3 9 t
Отже, 3 ≤ t ≤ 9
Тобто t ≥ 3; 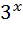 ≥ 3;
≥ 3; 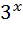 ≥
≥ 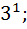
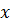 ≥ 1
≥ 1
t ≤ 9; 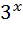 ≤ 9;
≤ 9; 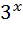 ≤
≤ 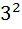 ;
; 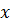 ≤ 2
≤ 2
1 2 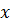
Відповідь: 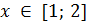
8) Розв’яжіть нерівність: 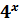 +
+ 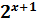 – 8 > 0
– 8 > 0
Замість 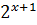 запишемо добуток
запишемо добуток 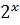 ∙ 2 та зведемо
∙ 2 та зведемо 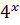 до степеня
до степеня
з основою 2:
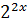 +
+ 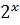 ∙ 2 – 8 > 0
∙ 2 – 8 > 0
Зробимо заміну змінної:
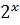 =
= 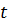 ,
, 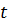 > 0, тоді
> 0, тоді 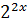 =
= 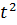
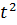 + 2
+ 2 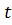 – 8 > 0
– 8 > 0
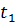 = – 4
= – 4
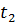 = 2
= 2
Розв’яжемо нерівність методом інтервалів:
( 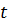 + 4) (
+ 4) ( 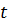 – 2) > 0
– 2) > 0
+ − +
−4 2 t
Враховуючи, що 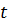 > 0, маємо :
> 0, маємо :
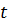 < −4;
< −4;
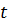 > 2;
> 2; 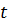 > 2,
> 2,
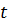 > 0;
> 0;
Отже, 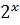 > 2
> 2
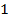 |
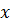 |

Відповідь: 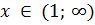 .
.
Вправи для самостійного розв’язування до теми 4:
Розв’яжіть нерівність:
1) 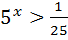 ; 11)
; 11) 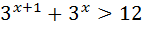 ;
;
2) 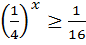 ; 12)
; 12) 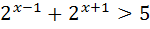 ;
;
3) 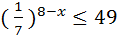 ; 13)
; 13) 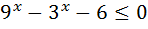 ;
;
4) 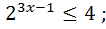 14)
14) 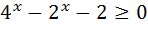 ;
;
5) 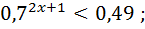 15)
15) 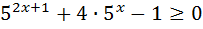 ;
;
6) 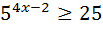 ; 16)
; 16) 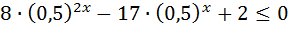 ;
;
7) 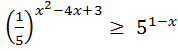 ; 17)
; 17) 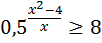 ;
;
8) 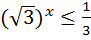 ; 18)
; 18) 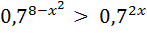 ;
;
9) 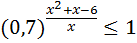 ; 19)
; 19) 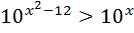 ;
;
10) 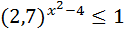 ; 20) 0,5
; 20) 0,5 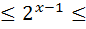 8 .
8 .
