Цель построения векторной диаграммы заключается в том, чтобы иметь возможность качественно контролировать аналитические расчеты электрических цепей синусоидального тока

Например, на векторной диаграмме напряжение на индуктивности должно опережать протекающий через нее ток на 90о, а на емкости напряжение должно отставать от тока на 90о.

Эти и другие возможные варианты соединения элементов отдельных участков электрических цепей, их сопротивления и значения (пределы изменения) углов сдвига фаз приводятся в табл. 1.1.

Таблица 1.1

Элементы	Сопротивление; полное комплексное сопротивление	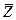Угол сдвига фаз между током и Напряжением	Векторная диаграмма
1.Резистор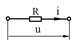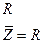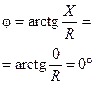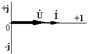
2.Катушка индуктивности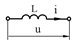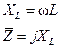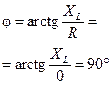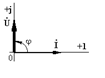
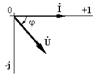
3.Конденсатор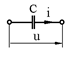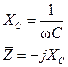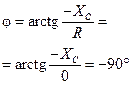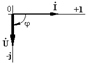
4.Резистор и катушка индуктивности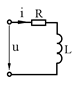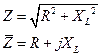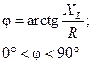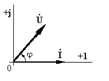

Окончание таблицы 1.2

Элементы	Сопротивление; полное комплексное сопротивление	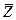Угол сдвига фаз между током и Напряжением	Векторная диаграмма
7. Резистор, катушка индуктивности и конденсатор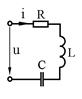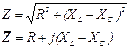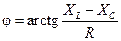

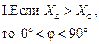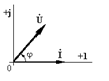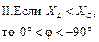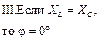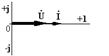Примечание: в п. 6 табл. 1.1 не рассматривается ведущий к возникновению неопределенности случай, когда .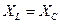

Обратите внимание, что:

Отсчет угла сдвига фаз всегда ведется от вектора тока. Если расчет дает результаты, не совпадающие с положениями табл. 1.1, следовательно, в него вкралась ошибка.

2) Векторная диаграмма позволяет зафиксировать положение вращающихся векторов для определенного момента времени. В электротехнике принято, что векторная диаграмма строится для нулевого момента времени (t = 0). Построение векторной диаграммы для любого другого момента времени может привести к изменению положения векторов относительно осей комплексной плоскости, однако взаимное расположение векторов останется неизменным.

1.8. Полная комплексная мощность

Рассмотрим прием определения активной и реактивной мощностей через комплекс напряжения и сопряженный комплекс тока.

Выше было показано, что токи и напряжения на различных участках электрической цепи синусоидального тока могут не совпадать по фазе.

Пусть к некоторому участку цепи приложено напряжение 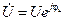. Тогда ток, протекающий по этому же участку, 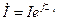. Умножив комплекс напряжения на сопряженный комплекс тока 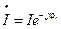, получим комплекс полной мощности (полную комплексную мощность)

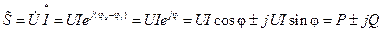,(1.27)

где значок ~ (тильда) над S означает комплекс полной мощности; Р – активная мощность; Q – реактивная мощность.

При этом активная мощность 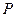является действительной частью полной комплексной мощности 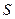, а реактивная мощность 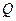- ее мнимой частью и обозначаются соответственно:

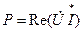, (1.28)

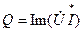. (1.29)

В (1.27) знак перед 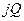определяется характером сопротивления на данном участке цепи и зависит от угла 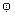. Очевидно, что знак «плюс» перед 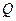ставится, если 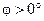, что возможно при выполнении условия 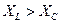; и знак «минус» - если 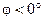, что возможно при выполнении условия .

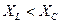Следует отметить, что единицей измерения активной мощности Р является ватт (Вт); единицей измерения реактивной мощности Q - вольт-ампер реактивный (ВАр); единицей измерения полной мощности S - вольт-ампер (ВА).

2. РАСЧЕТ РАЗВЕТВЛЕННОЙ ЦЕПИ синусоИДАЛЬНОГО

ПЕРЕМЕННОГО тОКА МЕТОДОМ КОМПЛЕКСНЫX ЧИСЕЛ

2.1. Условие расчетного задания №1. Варианты задания

В соответствии с вариантом задания (табл.2.2) выполнить преобразование разветвленной цепи переменного тока, схема которой представлена на рис. 2.1. Условно указать направления токов и напряжений.

Пользуясь комплексным методом, определить токи в ветвях; проверить соблюдение баланса активной, реактивной и полной мощностей в цепи; определить коэффициент мощности цепи; построить совмещенную векторную диаграмму токов и напряжений на комплексной плоскости.

Параметры элементов цепи даны в табл. 2.1. Один из параметров электрической энергии, необходимый для расчета, задан в табл. 2.2.

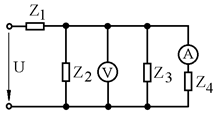
Рис. 2.1

На входе цепи (рис. 2.1) действует напряжение U. Приборы, показанные на рис. 2.1, измеряют следующие параметры: вольтметр – напряжение на разветвленном участке цепи, приложенное одновременно ко второй, третьей и четвертой ветвям (в табл. 2.2 это напряжение обозначено как U₂); амперметр – силу тока в четвертой ветви (в табл. 2.2 обозначен как ток I₄).

Таблица 2.1

Варианты	R, Ом	XL, Ом	XC, Ом
с 1 по 30
с 31 по 60
с 61 по 90
с 91 по 120
с 121 по 150

Таблица 2.2

Варианты	Z1	Z2	Z3	Z4	U, B	U2, B	I4, A	UC, B
1,31,61,91,121					-	-	-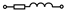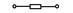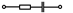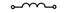
2,32,62,92,122					-	-		-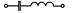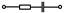
3,33,63,93,123					-	-	-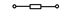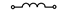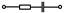
4,34,64,94,124					-		-	-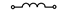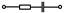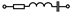
5,35,65,95,125						-	-	-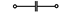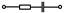
6,36,66,96,126					-	-	-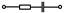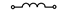
7,37,67,97,127						-	-	-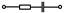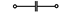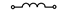
8,38,68,98,128					-	-	-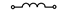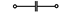
9,39,69,99,129					-	-		-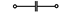
10,40,70,100,130					-		-	-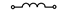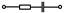
11,41,71,101,131					-	-	-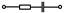
12,42,72,102,132						-	-	-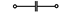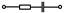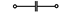
13,43,73,103,133					-	-		-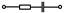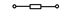
14,44,74,104,134					-		-	-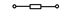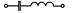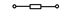
15,45,75,105,135						-	-	-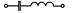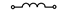

Окончание табл. 2.2

Варианты	Z1	Z2	Z3	Z4	U, B	U2, B	I4, A	UC, B
16,46,76,106,136					-		-	-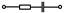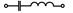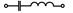
17,47,77,107,137					-	-	-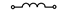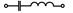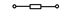
18,48,78,108,138					-		-	-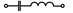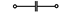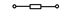
19,49,79,109,139						-	-	-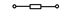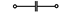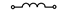
20,50,80,110,140					-	-		-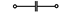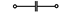
21,51,81,111,141					-	-	-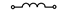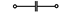
22,52,82,112,142						-	-	-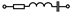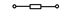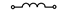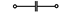
23,53,83,113,143					-		-	-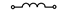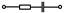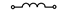
24,54,84,114,144				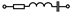	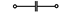-	-	1,5	-
25,55,85,115,145						-	-	-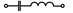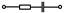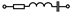
26,56,86,116,146		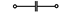			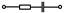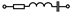-	-	2,5	-
27,57,77,117,147					-	-	-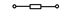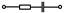
28,58,88,118,148					-		-	-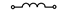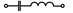
29,59,89,119,149					-	-		-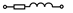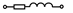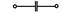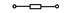
30,60,90,120,150					-		-	-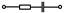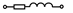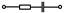

Примечание: знак означает, что в данном варианте задания указанная ветвь отсутствует.

2.2. Пример решения расчетного задания №1. Методика расчета.

Алгоритмы решения

Выполнить преобразование разветвленной цепи переменного тока, схема которой представлена на рис. 2.1, в соответствии с рис. 2.2, условно указать направления токов и напряжений. Известными являются следующие параметры: активное сопротивление (R = 2 Ом); индуктивное сопротивление (X_L = 6 Ом); емкостное сопротивление (X_C = 10 Ом); напряжение на разветвленном участке цепи (U₂ = 60 B).

Пользуясь комплексным методом, определить токи в ветвях; проверить соблюдение баланса активной, реактивной и полной мощностей в цепи; определить коэффициент мощности схемы; построить совмещенную векторную диаграмму токов и напряжений на комплексной плоскости.

Дано:

R = 2 Ом;

X_L = 6 Ом;

X_C = 10 Ом;

U₂ = 60 B

Найти: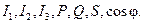

Решение:

1. Выполняем преобразование схемы, представленной на рис. 2.1, в соответствии с рис. 2.2. Четвертая ветвь на рис. 2.3 отсутствует, поскольку ее полное сопротивление равно бесконечности. Направления токов и напряжений условно указаны на рис. 2.3.

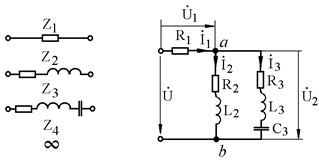
Рис. 2.2 Рис. 2.3

2. На основании законов Кирхгофа записываем уравнения для цепи, схема которой представлена на рис. 2.3. Обозначим число узлов буквой У, число ветвей буквой В.Количество уравнений, составляемых по первому закону Кирхгофа, равно (У-1).Количество уравнений, составляемых по второму закону Кирхгофа, равно числу ветвей В. Общее количество уравнений, составляемых по законам Кирхгофа, определяют по формуле:

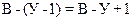. (2.1)

Схема, представленная на рис. 2.3, состоит из трех ветвей (В = 3) иимеет два узла (а и b), число узлов (У=2).Следовательно, по первому закону Кирхгофа необходимо записать одно уравнение, а по второму – три, тогда общее количество уравнений определяем по формуле (2.1):

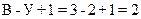. (2.2)

На основании первого закона Кирхгофа для узла а (см. рис. 2.3) можем записать

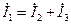, (2.3)

где 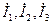- комплексные токи первой, второй и третьей ветвей соответственно.

Из рис. 2.3 видно, что вторая и третья ветви соединены параллельно, поэтому на основании второго закона Кирхгофа можем записать

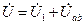, (2.4)

где 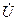- комплексное напряжение, подводимое к цепи от источника; 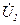- комплексное падение напряжения на первой ветви; 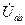- напряжение между узлами a и b (см. рис. 2.3).

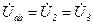, (2.5)

где 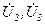- комплексные падения напряжения на второй и третьей ветвях соответственно.

3. На основании формулы (1.21) и рис. 2.3 запишем полные комплексные сопротивления ветвей:

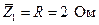; (2.6)

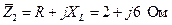; (2.7)

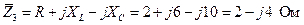. (2.8)

4. Определяем комплексные токи второй и третьей ветвей по закону Ома:

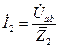; (2.9)

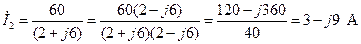; (2.10)

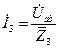; (2.11)

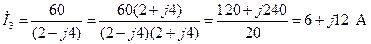. (2.12)

5. На основании выражения (2.3), записанного по первому закону Кирхгофа для узла а (см. рис. 2.3), определяем комплексный ток первой ветви

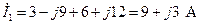. (2.13)

6. Определяем действующие значения токов, которые находим путем извлечения квадратного корня из суммы квадратов действительной и мнимой частей:

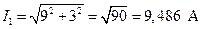; (2.14)

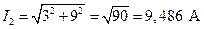; (2.15)

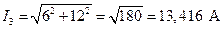. (2.16)

7. Определяем комплексное падение напряжения на первой ветви:

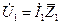; (2.17)

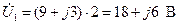. (2.18)

8. На основании выражения (2.4), записанного по второму закону Кирхгофа для схемы (см. рис. 2.3), определяем комплексное напряжение, подводимое к цепи:

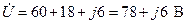. (2.19)

9. Определяем полную комплексную мощность, потребляемую схемой от источника:

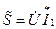; (2.20)

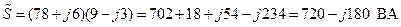.(2.21)

10. Составляем баланс мощности. Считают, что баланс мощности сходится, если полная комплексная мощность, потребляемая от источника, равна сумме комплексных мощностей всех ветвей цепи:

Активные мощности ветвей определяем следующим образом:

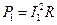; (2.22)

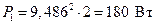; (2.23)

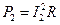; (2.24)

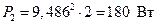; (2.25)

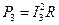; (2.26)

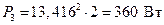. (2.27)

Определяем реактивные мощности ветвей. Реактивные элементы в первой ветви отсутствуют, поэтому можем записать

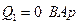. (2.28)

Для второй и третьей ветви получим

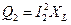; (2.29)

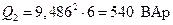; (2.30)

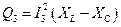; (2.31)

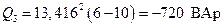. (2.32)

Составляем баланс активной и реактивной мощностей:

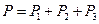; (2.33)

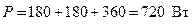; (2.34)

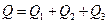; (2.35)

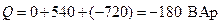. (2.36)

Сравнив результат проведенного выше расчета с данными п.10, видим, что баланс мощностей сходится как по активной, так и по реактивной мощностям.

11. Определяем коэффициент мощности цепи:

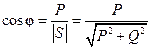; (2.37)

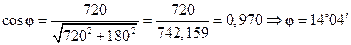. (2.38)

12. Строим совмещенную векторную диаграмму токов и напряжений на комплексной плоскости (рис. 2.4). Масштабы: по току 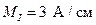; по напряжению .

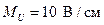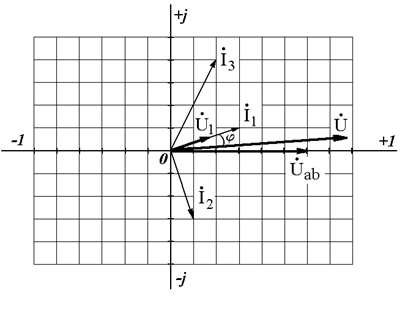
Рис. 2.4

Напомним, что в каждом отдельном варианте известен только один из параметров U, U₂, I₄, U_C. В п. 2.1 рассмотрены методика и алгоритм решения для случая, когда известным является напряжение U₂. Алгоритмы решения для других возможных вариантов необходимо выбрать из табл. 2.3.

Таблица 2.3

U	I4	UC
Конденсатор уста-новлен в первой ветви	Конденсатор уста-новлен в первой ветви	Конденсатор уста-новлен в первой ветви
	-
	-	-	-	-
	-	-	-	-

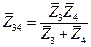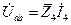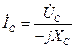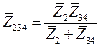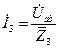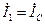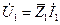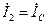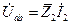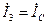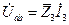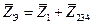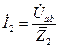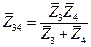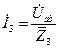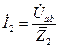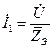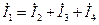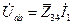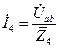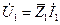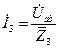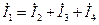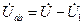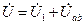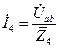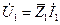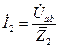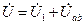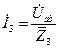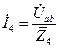Примечание: 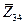-полное комплексное сопротивление параллельно соединенных третьей и четвертой ветвей; 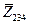-полное комплексное сопротивление параллельно соединенных второй, третьей и четвертой ветвей; 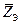- эквивалентное полное комплексное сопротивление всей цепи.

Следует отметить, что методика расчета баланса мощностей, рассмотренная в п. 2.2, является общей для всех вариантов.

2.3. Примерный перечень контрольных вопросов при защите расчетного задания №1

1. Что такое комплексное число? В каких формах записи могут быть представлены комплексные числа?

2. Какие действия можно производить над комплексными числами? Какая форма записи комплексных чисел является более удобной для каждого из рассмотренных действий?

3. В чем заключается сущность расчета электрических цепей синусоидального переменного тока методом комплексных чисел?

4. Задавшись законом изменения тока 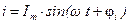, изобразите его в виде вектора на комплексной плоскости. Чем определяется длина этого вектора?

5. Задавшись значениями активного сопротивления R, индуктивности L и емкости C, запишите комплексное сопротивление 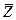в алгебраической и показательной формах.

6. Что такое угол сдвига фаз между током и напряжением, от чего он зависит?

7. Что такое совмещенная векторная диаграмма на комплексной плоскости? Какова цель ее построения?

8. Почему при построении векторной диаграммы на комплексной плоскости откладывают токи и напряжения и не откладывают комплексные сопротивления?

9. Запишите и объясните выражение закона Ома в комплексной форме.

10. Запишите и объясните выражение первого закона Кирхгофа в комплексной форме.

11. Запишите и объясните выражение второго закона Кирхгофа в комплексной форме.

12. Запишите и объясните выражение для полной мощности в комплексной форме.

13. Объясните алгоритм решения расчетного задания №1 для своего варианта.

14. Объясните, как определяется количество уравнений, записываемых на основании законов Кирхгофа, для схемы своего варианта.

15. Объясните методику проверки баланса мощностей.

16. Объясните методику построения векторной диаграммы для своего варианта.

Библиографический список к первому и второму разделам

1. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов. М.: Энергоатомиздат, 2000. С. 37-87.

2. Рекус Г.Г., Белоусов А.И. Сборник задач по электротехнике и основам электроники. М.: Высш. школа, 1991. С. 78-83, 89-98, 110-140.

3. ТРЕXФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

3.1. Трехфазная система питания потребителей электроэнергии.

Расширение понятия «фаза». Расчет трехфазных цепей

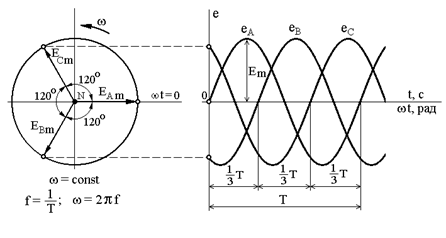
Трехфазный симметричный источник питания представляет собой совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на треть периода (на угол 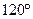). Законы изменения этих ЭДС во времени могут быть представлены следующими выражениями:

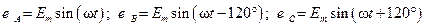. (3.1)

Временные диаграммы ЭДС трехфазного симметричного источника представлены на рис. 3.1 б. На рис. 3.1 а эти ЭДС представлены в виде вращающихся векторов на плоскости.

а б

Рис. 3.1

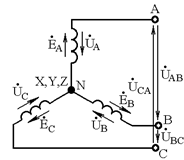
В качестве трехфазных источников чаще всего используются трехфазные генераторы. На электрических схемах трехфазный генератор принято изображать в виде трех обмоток, расположенных друг к другу под углом 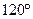. Каждая обмотка имеет начало и конец. Так, начало первой обмотки обозначают буквой А, конец – буквой X;начало второй - буквой В, конец – буквой Y; начало третьей - буквой С, конец - буквой Z(см. рис. 3.2 а).

а б

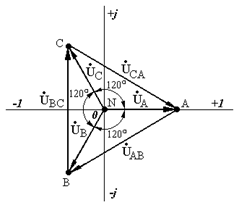
Рис. 3.2

Как уже было сказано, генератор принято называть источником, а обмотки генератора - фазами источника. Потребитель электроэнергии является нагрузкой для источника, поэтому потребителя принято называть нагрузкой. Под действием напряжений источника по фазам нагрузки протекают токи, сдвинутые относительно друг друга по фазе.

Под фазой трехфазной цепипонимают участок, по которому протекает один и тот же ток. Фаза имеет начало и конец. Фазой называют также аргумент синусоидальной функции. Таким образом, в зависимости от рассматриваемого вопроса фаза – это либо участок цепи, либо аргумент синусоидально изменяющейся функции.

Пренебрегая внутренними сопротивлениями источника, можно принять соответствующие ЭДС источника равными напряжениям, действующим на его зажимах:

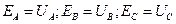. (3.2)

Комплексные фазные напряжения симметричного источника могут быть представлены в виде

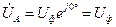; (3.3)

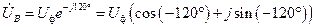; (3.4)

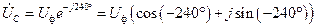, (3.5)

где 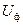- фазное напряжение источника.

На основании второго закона Кирхгофа могут быть определены комплексные линейные напряжения симметричного источника (см. рис. 3.2 а):

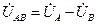; (3.6)

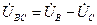; (3.7)

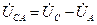. (3.8)

Для трехфазного симметричного источника справедливы следующие выражения:

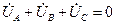; (3.9)

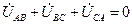. (3.10)

Условные направления фазных и линейных напряжений источника показаны на рис. 3.2 а. Между напряжениями трехфазного симметричного источника существуют следующие соотношения:

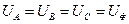; (3.11)

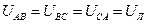; (3.12)

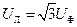, (3.13)

где 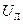- линейное напряжение источника.

Векторная диаграмма напряжений трехфазного симметричного источника на комплексной плоскости представлена на рис. 3.2 б.

Трехфазные цепи являются разновидностью цепей синусоидального тока, поэтому их расчет может быть произведен с использованием рассмотренного в разд.1 метода комплексных чисел. Отметим, что расчет трехфазных цепей с помощью указанного метода также сопровождается построением совмещенной векторной диаграммы.

3.2. Трехфазные трехпроводные цепи при соединении фаз нагрузки «звездой»

Схема трехфазной трехпроводной цепи при соединении нагрузки «звездой» показана на рис. 3.3. Цепь названа трехпроводной по количеству проводов, соединяющих нагрузку с источником.

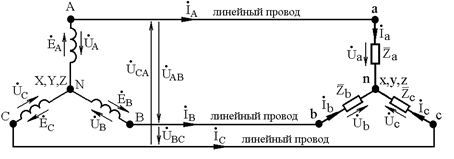
Рис. 3.3

При соединении фаз источника «звездой» концы обмоток X, Y, Zсоединяют в одну точку (см. рис. 3.3), которую называют нейтральной точкой источникаN. Началаобмотокисточника обозначают буквамиA,B,C.

Аналогично при соединении нагрузки «звездой» концы фаз x, y, zсоединяют в одну точку, которую называют нейтральной точкой нагрузкиn. Началафаз нагрузки обозначают буквамиa,b,c.

Фазы нагрузки на рис. 3.3 показаны в виде комплексных сопротивлений 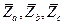. Нагрузка подключается к источнику с помощью соединительных проводов Аа,Bb, Cc,называемыхлинейными.

Здесь и далее условимся параметры, относящиеся к фазам источника, обозначать индексами 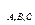, а параметры, относящиеся к фазам нагрузки, - индексами .

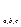По линейным проводам протекают линейные токи 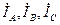, условное направление которых показано на рис. 3.3.

Пренебрегая сопротивлением линейных проводов, считаем, что к фазам нагрузки приложены напряжения, равные фазным напряжениям источника:

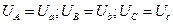, (3.14)

а между линейными проводами действуют линейные напряжения

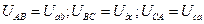. (3.15)

Под действием напряжений 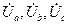по соответствующим фазам нагрузки 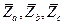протекают фазные токи 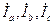, условное направление которых показано на рис. 3.3.

Фазные токи нагрузки могут быть определены на основании закона Ома:

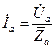; (3.16)

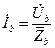; (3.17)

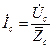. (3.18)

Запишем уравнения по первому закону Кирхгофа для узлов a, b, cсоответственно

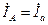; (3.19)

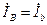; (3.20)

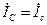. (3.21)

На основании (3.19)-(3.21) можем записать

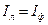. (3.22)

Выше было показано, что трехфазные источники, как правило, являются симметричными. При этом нагрузка трехфазного источника может быть симметричной или несимметричной.

Нагрузка является симметричнойпри выполнении условия

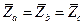. (3.23)

Для симметричной нагрузки справедливыми являются соотношения (3.13) и (3.22), а также равенства:

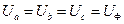; (3.24)

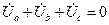. (3.25)

Векторная диаграмма напряжений для симметричной нагрузки при соединении фаз «звездой» показана на рис. 3.4 а. Анализ диаграммы показывает, что нейтральная точка нагрузки n совпадает с нейтральной точкой источника N, а фазные напряжения нагрузки равны фазным напряжениям источника в соответствии с условием (3.14).

При несимметричной нагрузке

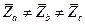, (3.26)

поэтому нарушается соотношение (3.13), не выполняется равенство (3.24), а сумма комплексов фазных напряжений по (3.25) дает число, отличное от нуля. В результате нейтральная точка нагрузки n смещается относительно нейтральной точки источника N в сторону той фазы, по которой протекает наибольший ток, а между нейтральными точками нагрузки и источника появляется напряжение смещения нейтрали :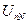

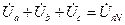. (3.27)

Это приводит к перекосу фазных напряжений нагрузки. В таких случаях говорят, что нарушается симметрия фазных напряжений нагрузки.

Фазные напряжения источника и фазные напряжения нагрузки будут связаны следующими соотношениями:

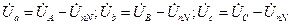. (3.28)

Векторная диаграмма напряжений для несимметричной нагрузки при соединении фаз «звездой» показана на рис. 3.4 б.

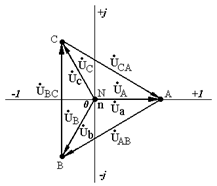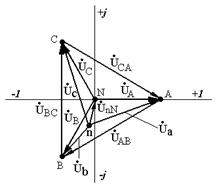а б

Рис. 3.4

Векторная диаграмма для трехфазных цепей также может быть выполнена совмещенной, то есть на одной комплексной плоскости откладывают векторы фазных токов и напряжений. Если нагрузка соединена «звездой», то векторы фазных токов откладывают из точки n независимо от условий нагружения (симметричная или несимметричная нагрузка), учитывая угол сдвига 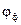между током и напряжением соответствующей фазы. Значение угла 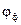зависит от характера сопротивления данной фазы и определяется по формуле (1.26). В остальном методика построения векторных диаграмм не отличается от методики, описанной в разд. 1.8, справедливыми являются также рекомендации табл. 1.1.

Следует отметить, что для трехфазной трехпроводной цепи независимо от условий нагружения справедливо следующее выражение

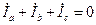. (3.29)

3.3. Трехфазные четырехпроводные цепи при соединении фаз нагрузки «звездой»

Недостатком трехфазных трехпроводных цепей является нарушение симметрии фазных напряжений при несимметричной нагрузке.

От этого недостатка свободны трехфазные четырехпроводные цепи.

На рис. 3.5 показана схема трехфазной четырехпроводной цепи при соединении нагрузки «звездой». Отличительной особенностью данной цепи является наличие четвертого – нейтральногопровода, соединяющего нейтральные точки нагрузки и источника.

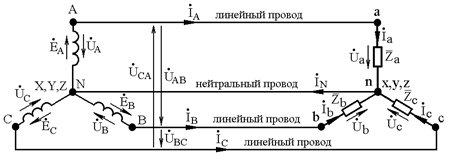
Рис. 3.5

Для схемы, представленной на рис. 3.5, независимо от условий нагружения справедливы соотношения: (3.13), (3.22), (3.24) и (3.25).

На основании первого закона Кирхгофа для узла n можем записать

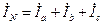. (3.30)

В случае симметричной нагрузки токи фаз будут равны по величине и сдвинуты по фазе на угол 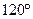. Тогда на основании (3.29) и (3.30) получим:

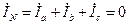. (3.31)

Очевидно, что в данном случае нейтральный провод никак себя не проявляет, поскольку ток в нем отсутствует.

В случае несимметричной нагрузки токи фаз будут отличаться по величине, кроме того, изменится угол сдвига фаз между током и напряжнием. Тогда на основании (3.30) получим:

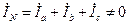. (3.32)

Сопоставив (3.31) и (3.32), можем сделать вывод: наличие нейтрального провода, по которому протекает ток 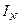, позволяет обеспечить несимметричную трехфазную нагрузку симметричным питанием.

3.4. Трехфазные электрические цепи при соединении фаз нагрузки «треугольником»

Схема трехфазной трехпроводной цепи при соединении нагрузки «треугольником» показана на рис. 3.6.

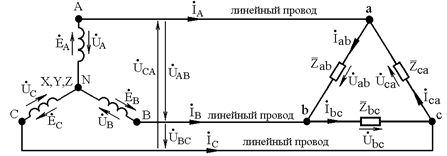
Рис. 3.6

При соединении нагрузки «треугольником» конец первой фазы хсоединяется с началом второй фазы b, конец второй фазы y -с началом третьей фазы с, конец третьей фазы z -с началом первой фазы а.

Фазы нагрузки на рис. 3.6 показаны в виде комплексных сопротивлений 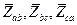. Нагрузка подключается к источнику с помощью линейных проводов, по которым протекают линейные токи.

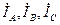Пренебрегая сопротивлением линейных проводов, считаем, что к фазам нагрузки приложены напряжения, равные линейным напряжениям источника

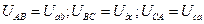. (3.33)

Под действием напряжений 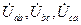по соответствующим фазам нагрузки 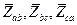протекают фазные токи 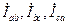, условное направление которых указано на рис. 3.6.

Фазные токи нагрузки могут быть определены на основании закона Ома:

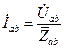; (3.34)

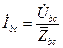; (3.35)

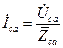. (3.36)

Запишем уравнения по первому закону Кирхгофа для узлов a, b, cсоответственно:

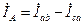; (3.37)

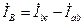; (3.38)

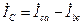. (3.39)

Для соединения нагрузки «треугольником» справедливо соотношение

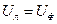. (3.40)

При симметричной нагрузке справедливыми являются следующие соотношения:

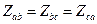; (3.41)

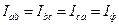; (3.42)

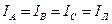; (3.43)

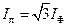. (3.44)

В рассмотренных выше примерах фазы источника были соединены «звездой», однако возможно также соединение фаз источника «треугольником». При этом конец первой фазы Xсоединяется с началом второй фазы В, конец второй фазы Y - с началом третьей фазы C, конец третьей фазы Z -с началом первой фазы A.

3.5. Активная, реактивная и полная мощности трехфазной цепи

Полную комплексную мощность одной фазы трехфазной цепи можно определить, умножив комплекс фазного напряжения на сопряженный комплекс тока этой фазы:

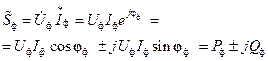(3.45)

где 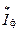- комплексный ток, сопряженный комплексному току фазы.

Формула (3.45) справедлива как для соединения фаз нагрузки «звездой», так и для соединения «треугольником», независимо от условий нагружения.

При этом активная мощность 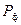является действительной частью полной комплексной мощности 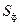, а реактивная мощность 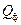- ее мнимой частью, которые обозначаются соответственно:

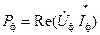; (3.46)

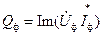. (3.47)

В (3.45) знак перед 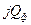определяется характером сопротивления данной фазы и зависит от угла 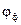, величину которого можно определить по формуле (1.26). Очевидно, что знак «плюс» перед 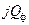ставится, если 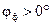, что возможно при выполнении условия 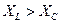; и знак «минус» - если 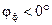, что возможно при выполнении условия .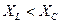