Аналогично преобразуем и уравнение движения
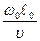 (Wx
(Wx 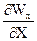 + Wу
+ Wу 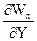 ) =
) = 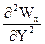 +
+ 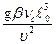 ×
× 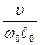 ×Q
×Q
Rе º w0 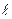 0/n -число Рейнольдса – характеризует соотношение сил инерции и сил вязкости
0/n -число Рейнольдса – характеризует соотношение сил инерции и сил вязкости
Gr º gbuc 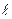 03/n2 -число Грасгофа – характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей
03/n2 -число Грасгофа – характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей
Известно, что коэффициент теплоотдачи при известном температурном поле определяется по уравнению:
a = - 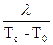 (
( 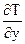 )у=0
)у=0
Приведя к записи в безразмерной форме, получим
Þ a 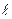 0/l = - (¶Q/¶Y)Y=0
0/l = - (¶Q/¶Y)Y=0
Nu º a 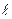 0/l -число Нуссельта или безразмерный коэффициент теплоотдачи – характеризует теплообмен на границе стенка - жидкость
0/l -число Нуссельта или безразмерный коэффициент теплоотдачи – характеризует теплообмен на границе стенка - жидкость
Pr = n/a –число Прандтля Þ мера подобия полей температур и скоростей (а = l/сr)
Þ Ре = Rе ×Pr
при Pr = 1
Уравнение сплошности в безразмерной форме имеет вид
w0  0(¶Wx/¶Х + ¶Wy/¶Y) = 0
0(¶Wx/¶Х + ¶Wy/¶Y) = 0
Граничные условия
1) Y = ¥ Þ Q = Qс = 0; Wx = 1; Wy = 0
2) Y = 0 Þ Q = Qс = 1; Wx = Wy = 0
Таким образом, мы получили систему безразмерных дифференциальных уравнений и безразмерных условий однозначности.
В итоге имеем: Х и Y – независимые переменные; Nu, Q, Wx, Wy – зависимые переменные; Ре, Rе, Gr – постоянные величины.
В результате можно записать уравнения подобия:
Nu = f1(Хc,Yc, Ре, Rе, Gr);
Q = f2(Хc,Yc, Ре, Rе, Gr);
Wx = f3(Хc,Yc, Ре, Rе, Gr);
Wy = f4(Хc,Yc, Ре, Rе, Gr);
Критерии подобия – это числа подобия, составленные из наперед заданных параметров (постоянных) математического описания процесса.
Условия подобия физических процессов
Полученная система безразмерных дифференциальное уравнений, так же как и исходная система размерных уравнений, описывает бесконечное множество конкретных процессов конвективного теплообмена.
Те явления природы, которые описываются одинаковыми по форме записи дифференциальное уравнениями, но различны по своему физическому содержанию, называются аналогичными (например аналогия электрических и тепловых явлений).
В 1931 г. Кирпичев Михаил Викторович сформулировал условия подобия физических процессов (теорема Кирпичева):
1. Подобные процессы должны быть качественно однородными, то есть они должны иметь одинаковую физическую природу и описываются одинаковыми по форме записи дифференциальное уравнениями.
2. Условия однозначности подобных процессов должны быть одинаковы во всем, кроме числовых значений размерных постоянных, содержащихся в этих условиях.
3. Одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение (то есть дифференциальное уравнения и условия однозначности в безразмерном виде одинаковы для подобных процессов).
Следствия из условий подобия
Если процессы А и Б подобны, то любая физическая величина j в данной точке процесса А пропорциональна соответствующей величине в сходственной точке процесса Б, то есть:
jА = сj×jБ,
где сj - константа подобия.
Таким образом, подобные процессы можно рассматривать, как один и тот же процесс, но взятый в различном масштабе, причем масштабы разноименных величин могут быть одинаковыми.
Теория подобия позволяет моделировать процессы конвективного теплообмена.
Обработка результатов опыта
Теория подобия дает возможность ответить на следующие важные вопросы, возникающие при планировании эксперимента, обработке опытных данных и использовании эмпирических результатов:
- какие величины надо измерять в опыте;
- как обрабатываются результаты опыта;
- в каких пределах можно пользоваться полученной эмпирической зависимостью.
Три теоремы подобия и следствия из них дают ответ на поставленные вопросы:
1) В опытах нужно измерять те параметры, которые входят в числа подобия изучаемого явления;
2) Результаты опыта следует обрабатывать так, чтобы получить уравнение подобия – функциональную зависимость между числами подобия;
3) Уравнения подобия справедливы для всех подобных явлений.
Для изучения способов построения критериальных зависимостей по конвективному теплообмену рассмотрим некоторые параметры, входящие в числа подобия – определяющую температуру и определяющий размер.
Многие параметры (n, l, r и т.д.), входящие в числа подобия, существенно зависят от температуры. Температура же самой жидкости при свободной конвекции изменяется от температуры стенки Т до температуры среды в области, удаленной от стенки Тс. Поэтому в технических расчетах принято выбирать значения параметров при некотором осредненном значении температуры, названном определяющей температурой. В процессах со свободной конвекцией в качестве определяющей температуры Тm часто принимают среднеарифметическое значение
Тm = 0,5(Т + Тс)
Коэффициент конвективной теплоотдачи зависит от геометрических параметров тела. Причем для разных случаев теплообмена число геометрических параметров, существенно влияющих на процесс, может изменяться.
Определяющим геометрическим размером для круглой трубы будет диаметр трубы d. При обтекании пластины за определяющий размер выбирается длина пластины по направлению движения.
Рассмотрим, как получают эмпирические формулы.
Прежде, чем обработать опытные данные в числах подобия, нужно установить, от каких чисел зависит определяемое значение.
1) Для этого составляется система дифференциальных уравнений, описывающих экспериментально изучаемый процесс, и формируются условия однозначности. Затем математическое описание приводится к безразмерному виду. Например, было получено, что
Nu = f(Rе, Рr)
2) По данным измерений подсчитывают значения Rе и Рr и соответствующее им значение Nu.
3) Зависимость между числами подобия обычно представляют в виде степенной функции
Nu = с Rеn Рrm,
где с, n, m – постоянные безразмерные числа.
Пусть Nu = с Rеn.
Логарифмируя это уравнение, получим:
lg Nu = lg c + n lg Re или Y = А + n Х –уравнение прямой линии.
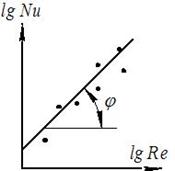
Показатель степени n представляет собой тангенс угла наклона прямой к оси абсцисс. Проверкой применимости степенной зависимости является то, что в логарифмических координатах все точки укладываются на прямую. Если же опытные точки располагаются по кривой, то эту кривую заменяют ломанной.
Для разных участков такой кривой значения c и n различны.
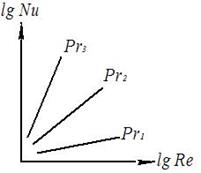
В случае если искомая величина Nu является функцией 2-х аргументов, например Nu = f(Rе, Рr), на графике получается семейство кривых. Для обработки опытных данных применяются ЭВМ.
Лекция № 8
