Дискретные случайные величины и основные законы их распределения.

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Случайной называют величину, принимающую в результате испытаний те или иные возможные значения, наперед неизвестные и зависящие от случайных причин, которые заранее не могут быть учтены.

Случайные величины обозначаются заглавными буквами латинского алфавита X, Y, Z и т. д. или заглавными буквами латинского алфавита с правым нижним индексом 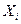, а значения, которые могут принимать случайные величины – соответствующими малыми буквами латинского алфавита x, y, z и т. д.

Понятие случайной величины тесно связано с понятием случайного события. Связь со случайным событием заключается в том, что принятие случайной величиной некоторого числового значения 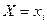есть случайное событие, характеризуемое вероятностью .

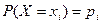На практике встречаются два основных типа случайных величин:

1. Дискретные случайные величины;

2. Непрерывные случайные величины.

Случайной величиной называется числовая функция от случайных событий.

Например, случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента.

Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.

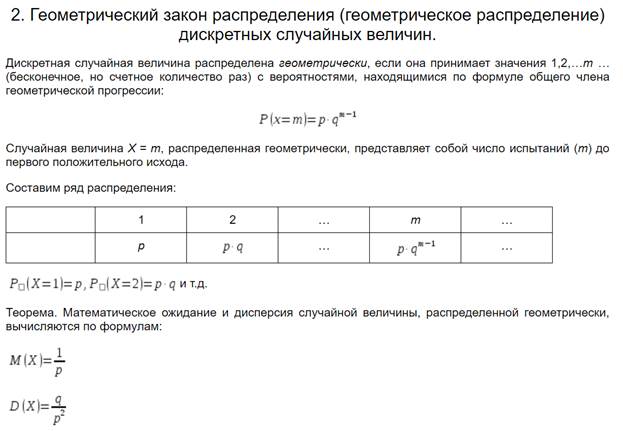
Непрерывные случайные величины и основные законы их распределения.

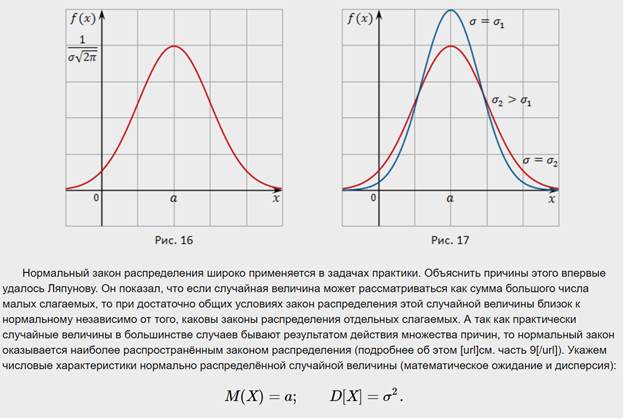
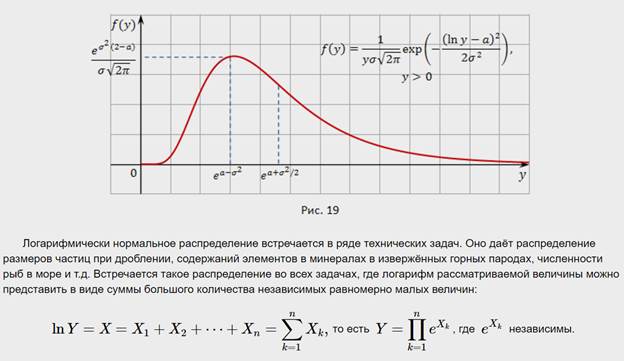
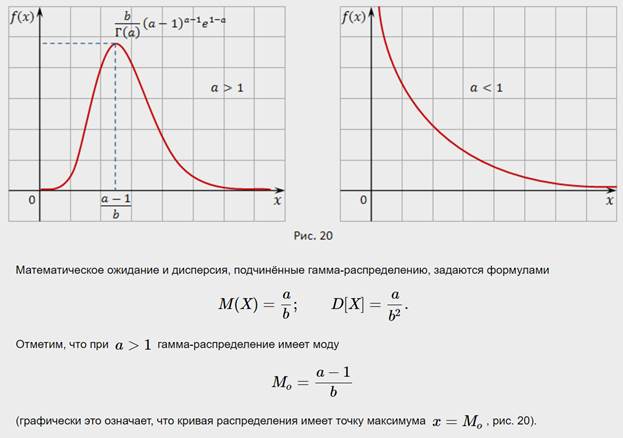
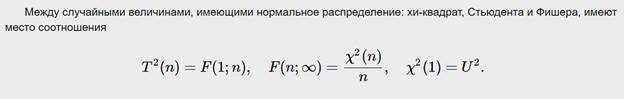
Числовые характеристики случайных величин и их свойства.

Случайные векторы.

Часто в вероятностных моделях случайных явлений приходится рассматривать сразу несколько случайных величин, причем изучение каждой случайной величины отдельно от других приводит к недопустимому упрощению модели явления. Математической моделью таких случайных явлений является понятие случайного вектора.

Определение. Совокупность случайных величин 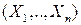, определенных на одном и том же вероятностном пространстве 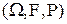, значения которых совместно описывают результат некоторого случайного эксперимента, называется 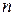-мерным случайным вектором (многомерной случайной величиной или системой случайных величин) и обозначается 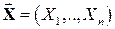. При этом сами случайные величины 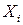, 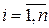называют координатами (компонентами, составляющими) случайного вектора .

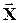Как и в одномерном случае, исчерпывающей вероятностной характеристикой случайного вектора является его функция распределения. Рассмотрим вначале случай двумерного случайного вектора 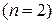, как наиболее часто встречающийся в практических приложениях, а потом полученные результаты обобщим на случай многомерный.

Двумерный случайный вектор обычно обозначают 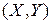(без введения индексов).