Теориялық бөлімі. Бұл әдіс жүйелерді синтездеу кезінде орнықтылықтың шарттары бойынша жүйенің кейбір параметрлерінің

Бұл әдіс жүйелерді синтездеу кезінде орнықтылықтың шарттары бойынша жүйенің кейбір параметрлерінің (әдетте күшейту коэффициенті k немесе реттегіштің тұрақты уақыты T) өзгеру кезіндегі рұқсат етілген шектерін анықтау үшін пайдаланылады.

D-бөліктеу дегеніміз - сипаттамалық теңдеудің оң түбірлерінің саны әр түрлі болып орналасқан аудандарын жүйе параметрлерінің кеңістігінде салу үрдісі.

D(0) - орнықтылық ауданы деп, өзгертілетін параметрлер кеңістігіндегі, әрбір нүктесіне сипаттамалық теңдеудің тек сол жақ түбірлері ғана сәйкес келетін ауданы аталады. Қалған D-аудандары сипаттамалық теңдеудің оң жақ түбірлері санымен ерекшеленеді және сәйкесінше: D(1) – бір оң полюсі бар аудан, D(2) – екі оң полюсі бар аудан және т.б. деп белгіленіледі. Орнықтылық ауданы өзгеретін параметрлердің барлық мүмкін боларлық мәндерінің ішінен, тек жүйе орнықты болатын мәндерін ғана көрсетеді. Орнықтылық ауданын шектейтін жазықтық беті – орнықтылық ауданының шекарасы деп аталады. Орнықтылық ауданы мен шекарасы өзгертілетін параметрлер санымен анықталады.

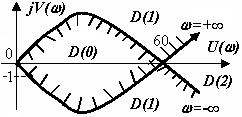
Кез - келген D-облыстың шекарасы түбірлер жазықтығындағы жорамал осьінің кескіні болып табылады, ол параметрлер мәнінің жиынтығына сәйкес келеді, яғни мұнда жүйенің сипаттамалық теңдеуінің кем дегенде бір түбірі жорамал осьте жатады.

Егер жүйе өзінің барлық параметрлерінің кеңістігінде орнықтылық облысына ие болмаса, онда ол құрылымды орнықты емес болып табылады. Тәжірибеде бір параметрі бойынша (нәтижесі болып шартты жазықтықтағы кесінді табылады) және екі параметрі бойынша (нәтижесі болып жазықтық табылады) D-бөліктеу әдісі пайдаланылады.

Бір параметрі бойынша D-бөліктеуі кезінде барлық салынулар тек бір параметрдің мәнін өзгерту арқылы жүзеге асырылады, ал қалғандары тұрақты болады. Жазықтық алу үшін заттық параметрді жасанды түрде екі өлшемді етеді, яғни s=j( ауыстырып, жорамал осьін қалыптастырады, бірақ нақты ось бойында орналасқан кесінді, шешуші нәтижесі болып табылады.

Жүйенің сипаттамалық теңдеуіне s = j( қойып, оны өзгертілетін параметріне қатысты шешеді, жұп (нақты) U(()және тақ (жорамал) V(() функцияларын анықтайды. Жиілікті ( нөлден шексіздікке дейін өзгерте отырып, D-бөліктеу қисығын және оның нақты осьіне қатысты айнабетті кескінін салады. Қисықбойымен ( = -( нүктесінен ( = +( нүктесіне дейін қозғала отырып, қисықтың сол жағынан сызықшалар (штрих) жасайды. (Ескертеміз: D-бөліктеу қисығы жорамал осьтің кескіні болып табылады, ал осы ось бойынша -j( -тен +j( -ке дейін қозғалғанда түбірлер жазықтығындағы орнықтылық облысы сол жақта орналасады).

Сызықшалар (штрихтар) бағыты сол жақ түбірлердің ең көп мөлшерде орналасқан ауданын көрсетеді. Қисық арқылы сызықшаларға қарай өткен әр кез сайын, сипаттамалық теңдеудің бір түбірі оң, кері бағытта – сол жақты болады. Таңдалған D(0) үміткер-облысын орнықтылыққа, осы ауданда жатқан параметр мәнін сипаттамалық теңдеуге қойып, кез - келген критерий арқылы тексеруге болады. Өзгертетін параметр нақты шама болып табылғандықтан, оның рұқсат етілген мәні орнықтылық облысының D(0) ішінде орналасқан нақты осьтің кесіндісінде жатыр.

Критикалық (сыни) деп - жүйе орнықтылық шекарасында болған кезіндегі сипаттамалық теңдеу коэффициентінің немесе жүйе параметрінің мәнін атаймыз.

Төртінші ретті жүйенің Үміткер-облысын D(0) орнықтылыққа тексеру үшін Гурвиц қағидасы ыңғайлы, мұнда екі шарт орындалуы керек:

1. Қажетті шарт – сипаттамалық теңдеудің барлық коэффициенттері оң болуы керек, a_i > 0;

2. Жеткілікті шарт – үшінші ретті анықтаушы нөлден үлкен болуы керек, (₃ = a₃(₂ – a₁²a₄ = a₃·(a₁(a₂ - a₀(a₃) – a₁²a₄ > 0.