Проверка статистических гипотез

Пусть Х – наблюдаемая СВ. Она может быть дискретной, а может и непрерывной.

Опр. Статистической гипотезой Н называется предположение относительно параметров или вида распределения СВ Х. Гипотеза Н называется простой, если она однозначно определяет распределение СВ Х, иначе Н называется сложной.

Если распределение СВ Х известно и по выборке наблюдений необходимо проверить предположение о значении параметров этого распределения, то такие гипотезы называются параметрическими. А гипотезы о виде распределения – непараметрические.

Проверяемая гипотеза называется нулевой гипотезой и обозначается Н₀. Обязательно на ряду с Н₀ рассматривают одну из альтернативных гипотез Н₁.

При этом имеются различные ситуации для Н₁.

; ; ; .

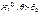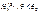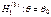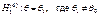Выбор альтернативной гипотезы Н₁ определяется конкретной формулировкой задачи.

Опр.Правило, по которому принимается решение принять или отклонить гипотезу Н₀, называется критерием К. Так как решение принимается на основе выборки наблюдений СВ Х, то необходимо выбрать подходящую статистику, которую мы будем называть статистикой Z критерия К.Замечание.При проверке простой параметрической гипотезы Н₀: q=q₀ в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра q, т.е. 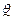.Основной принцип при проверке статистической гипотезы: Маловероятные события считаются невозможными, а события, имеющие большую вероятность, считаются достоверными. Реализация этого принципа на практике. Перед анализом выборки фиксируется некоторая малая вероятность a, называемая уровнем значимости. Пусть V множества значений статистики Z, V_K – подмножество множества значений статистики Z (V_K £ V). Это такое подмножество, что при условии истинности гипотезы Н₀, имеем вероятность того, что P{ZÎV_kïH₀}=a. Обозначим через z_в – выборочное значение статистики Z, которое вычитается по конкретной выборке. Критерии К формулируется следующим образом.

Отклонить гипотезу Н₀, если z_вÎV_k. Отклонить гипотезу Н₀, если z_вÎV \ V_k. Уровень значимости a определяет размер критической области, а ее положение зависит от альтернативной гипотезы Н₁.

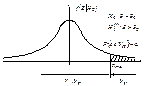
Z_1–a–квантиль распределения Z при условии, что верна гипотеза Н₀.

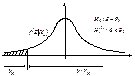
Z_a– квантиль распределения Z при условии, что верна гипотеза Н₀.

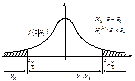
Проверку параметрической гипотезы при помощи критерия значимости можно разбить на следующие этапы:1)сформулировать Н₀ и Н₁;2)назначить a;3)выбрать статистику Z для проверки Н₀;4)определить выборочное распределение Z при условии, что верна Н₀;5)определить V_K (она зависит от Н₁);6)получить выборку и вычислить z_b ;7)принять статистическое решение: z_вÎV_k – отклонить Н₀;

z_вÎV \V_k – принять Н₀. Статистическое решение может быть ошибочным. При этом различают ошибки I-го и II-го родов.Опр. Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза Н₀ отклоняется, когда Н₀ – верна. Вероятность P{ZÎV_kïH₀}=a..ОпрОшибкой второго рода называется ошибка, состоящая в том, что принимается гипотеза Н₀, но в действительности верна альтернативная гипотеза Н₁. Вероятность ошибки второго рода при условии, что гипотеза Н₁ – простая, P{ZÎV\V_kïH₁}=b.Проверка статистических гипотез и доверительных интервалов.Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н₀ – принимается, если значение q₀ накрывается доверительным интервалом, иначе отклоняется.

2.Вероятностное пространство.Вероятность,ее свойства.Теорема сложения.Тройка (W, A, P), где W – это пространство элементарных событий;A – s-алгебра подмножеств W, называемых событиями;P – числовая функция, определенная на событиях и называемая вероятностью.P называется вероятностным пространством, если выполнены следующие аксиомы:1)P(A) ³ 0,"AÎA.2)P(W) = 1 (нормированность P).3)P(A+B)=P(A) + P(B), если A×B=Æ (аддитивность).4)Для любой убывающей последовательности A₁É A₂ É…É A_nÉ…событий из A такой, что , 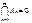Имеет место равенство 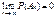(непрерывность P).Замечания: Аксиомы 3, 4 можно заменить одной аксиомой s-адди-тивности: 3*. Если события A_n в последовательности A₁, A₂, …попарно несовместны, то 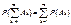Из этих аксиом вытекают Свойства вероятностей: 1)Если A Í B, то вероятность P(B–A) = P(B) – P(A). Доказательство: Разобьем событие B в сумму несовместных событий B=A+(B-A), A×(B-A)=Æ, P(B) = P(A+(B-A))=P(A)+P(B-A) (по аксиоме 3) P(B-A)=P(B) - P(A) ¢ . 2)Если A Í B, то P(A) £ P(B)Доказательство: Доказательство следует из 1 свойства и аксиомы 1. P(A) + P(B-A) = P(B) P(B-A) ³ 0, следовательно P(A) £ P(B) ¢. 3)"A Î A Þ 0 £ P(A) £ 1 Доказательство: A Í W Þ P(A) £ P(W), P(W) = 1(по аксиоме 2) P(A) ³ 0, "A Î A(по аксиоме 1) ¢. 4)P(Ā) = 1 - P(A) Доказательство: A+ Ā = W, A× Ā = Æ Тогда по аксиоме 3 и аксиоме 2 получаем P(A+ Ā) = P(W), P(A) + P(Ā) = P(W), P(A) +P(Ā) = 1 Þ P(Ā) = 1 - P(A) ¢. 5) P(Æ) = 0Доказательство:Æ + W = W Тогда по аксиоме 3 и 2 получаем, P(Æ) + P(W) = P(W) Þ P(Æ) + 1 = 1, P(Æ) = 0 ¢. 6)Теорема сложения "A, B Î A : P(A+B) = P(A) + P(B) – P(AB) Доказательство: A + B = A + (B - AB), A×(B - AB) = Æ P(A+B) = P(A) + P(B - AB), но AB Í B следовательно по первому свойству (вероятность от разности равна разности вероятностей). P(A+B) = P(A) + P(B) – P(AB) ¢. 4.Основные правила комбиноторики:«правило суммы» и «правило произведения» Комбинаторика – это наука о том, сколько различных комбинаций удовлетворяющих условиям можно составить на элементах конечного множества. Комбинаторные схемы: Правило суммы: X – конечное множество çXç=n – количество элементов. Объект x из X может быть выбран n-способами. Пусть X₁,…,X_k попарно непересекающиеся множества, то есть X_iÇX_j=Æ, i¹j тогда очевидно выполняется равенство. 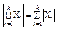– правило суммы Правило произведения:Если объект x может быть выбран m-способами и после каждого из таких выборов объект y может быть выбран n-способами. Тогда выбор упорядоченной пары (x,y) может быть осуществлен – m×n способами. Доказательство: Воспользуемся правилом суммы. {a₁,…,a_m}– множество элементов, из которых выбирается объект x."i=1,..,m,рассмотрим множество X_i={(a_i ,y)}, тогда первая компонента совпадает с a_i. Множества X_i попарно не пересекаются. çX_iç=n. Множество пар X_i-это объед. 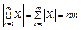В общем случае правило произведения формируется следующим образом: Если объект x₁ может быть выбран n₁ – способами, после чего объект x₂ может быть выбран n₂ способами и "i, где i=1,..,m-1 (2£ i £m-1) после выбора объектов x₁,…,x_i объект x_i+1 может быть выбран n_i+1-способами, то выбор упорядоченной последовательности x₁,…,x_m может быть осуществлен n₁,…,n_m способами. Доказательство проводится методом математической индукции.     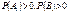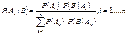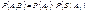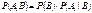10.Формулы Байеса Теорема.Если A₁,…,A_n – разбиение W и все , тогда имеет место следующая формула: Доказательство: По теореме умножения: 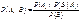Формулы Байеса можно интерпретировать следующим образом: назовём A_i – гипотезой, а B – результат некоторого эксперимента, a P(A_i) – априорные вероятности, а условные вероятности 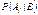–апостериорные вероятности (послеопытные вероятности).Формулы Байеса позволяют по априорным и условным вероятностям вычислить апостериорные вероятности гипотез. Пример:Детали, изготовленные цехом завода, попадают к одному из двух контролёров для проверки на стандартность. Вероятность того, что деталь попадёт к первому контролёру – 0,6; ко второму контролёру, соответственно, – 0,4. Вероятность того, что годная деталь будет признана стандартной, для первого контролёра – 0,9; для второго – 0,98. Годная деталь была признана стандартной. Найти вероятность того, что её проверил первый контролёр. Решение. A₁={деталь проверил первый} A₂={деталь проверил второй} A₁A₂=Æ, A₁+A₂=W B={годная деталь признана стандартной}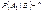 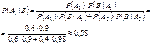11. Независимость событий Если события A иB таковы, что P(B)>0Þ$ P(A½B) Определение. Событие A не зависит от события B, если P(A½B) = P(A) Если потребовать условия P(A)>0, то 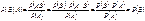Понятие того, что одно событие зависит от другого, симметрично. ЗамечаниеИз теоремы умножения: P(AB)=P(B)× P(A½B) P(AB)=P(B)× P(A) Это приводит к определению. ОпределениеСобытия A иB называются независимыми, если вероятность произведения событий равна произведению вероятностей событий (P(AB)=P(A)×P(B)). Если событие A не зависит от события B, то они являются просто независимыми. Если P(AB)=P(A)×P(B) не выполняется, то события являются зависимыми. P(AB)=P(A)×P(B)–теоретико-вероятностная (статистическая) независимость; её следует отличать от причинной независимости реальных явлений. Причинная независимость реальных явлений не устанавливается с помощью этого равенства, а постулируется на основе других внешних соображений. Определение (Независимость событий в совокупности) События A₁,…,A_n называются независимыми, если " индексов 1£i₁< i₂<…< i_m£n, где 2£m£n, то выполняется: 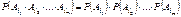В противном случае — события зависимы. Замечание.Из определения независимости событий в совокупности следует, что события любого подмножества 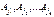множества A₁,…,A_n будут независимы в совокупности. Пример. Имеются 4 числа: 2, 3, 5, 30. Наудачу выбирается одно число. Вероятность этого события – 0,25. A_k={выбранное число делится на k}. Решение.P(A₂)=1/2; P(A₃)=1/2 ; P(A₅)=1/2; P(A₃₀)=1/2 P(A₂A₃)=1/4;P(A₂A₅)=1/4;P(A₃A₅)=1/4;P(A₂A₃A₅)=1/4 P(A₂A₃)=P(A₂)P(A₃) P(A₂A₅)=P(A₂)P(A₅) - попарно независимы P(A₃A₅)=P(A₃)P(A₅) P(A₂)P(A₃) P(A₅)=0.5*0.5*0.5=1/8 P(A₂A₃ A₅)=1/4 (в совокупности зависимы). Совокупная независимость более сильное свойство, нежели попарная независимость. Теорема.Если события A₁,…,A_n являются независимыми, индексы i₁,…,i_n , j₁,…,j_k – все различны, вероятность 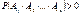, тогда:  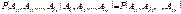 14. Непрерывная СВ. Плотность распределения. Опр.Функция 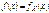есть плотность распределения СВ X, если 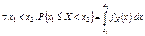(***) Из определения (***) следуют свойства плотности распределения. Свойства 1. 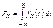Замечание. Для СВ X имеющей функции. Плотности из свойства 1 и теоремы из курса математического анализа (о непрерывности интеграла с переменным верхним пределом) Þ что 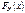непрерывна.   2. 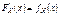в точках непрерывности 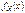. 3. . 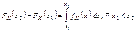4. 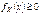, т.к. 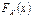неубывающая функция, то 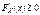. 5. Условия нормировки: 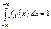. Опр. СВ X называется СВНТ, если ее распределение имеет функцию плотности 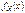. Через плотность 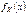можно выразить любую вероятность 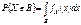17.Мода, медиана и квантили МО не единственная характеристика положения, применяемая в теории вероятностей. Опр. Модой СВДТ Х называется такое возможное значение x_m, для которого 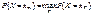=x_m. Модой СВНТ Х называется действительное число d_X, являющееся точкой максимума функции плотности вероятностей (f_X (x)) Пример. X 0 1 2 3 4 P 0,05 0,3 0,25 0,2 0,2 d_X=1 Замечание. Мода может не существовать, иметь единственное значение, такие распределения называются унимодальное, или иметь множества значений – полимодальное распределение. Наличие более чем одной моды, часто указывает на разнородность статистического материала, который положен в основу исследований. Опр.Медианой СВ Х называется действительное число h_X, удовлетворяющее условию: 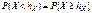, то есть это корень уравнения F_X (x)=1/2. Эта характеристика применяется, как правило, только для СВНТ и геометрически медиана, это абсцисса той точки на оси ОХ, для которой площади под графиком f_X(x)лежащие слева и справа от нее одинаковы и равны 1/2 Замечание. В случае симметричного распределения (имеющего моду) три характеристики: 1) МО ; 2) мода; 3) медиана совпадают. Замечание. Уравнение F_x(x)=1/2 может иметь множество корней, поэтому медиана может определяться неоднозначно. Опр. Квантильлью порядка р распределения СВНТ Х называется действительное число t_p, удовлетворяющее уравнению P{X<t_p}=p Замечание. Медиана h_x=t_0,5 – квантиль порядка 0,5. 22.Локальная предельная теорема Муавра-Лапласа. Биномиальное распределение имеет МО равное np 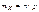. 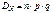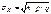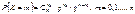Пусть p – не близко к 0 и 1. Теорема. Если в схеме независимых испытаний 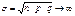, то для любого C>0 равномерно по всем 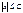вида 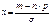, где m – неотрицательные целые числа 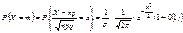Замечание. 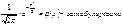Эти таблицы даются, только для x>0. 18.Целочисленные СВ и их производящие функции В ряде случаев при определении важнейших числовых характеристик дискретных СВ может помочь аппарат производящих функций. Опр. Дискретную СВ Х, принимающую только целые, неотрицательные значения называют целочисленной СВ. Закон распределения целочисленной СВ определяется 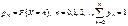. Закон распределения целочисленной СВ удобно изучать с помощью производящей функции, которая определяется, как 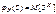. В соответствии с определением МО: 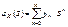. Этот ряд сходится абсолютно при 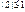. Поскольку 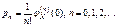, то между законом распределения 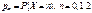и производящими функциями 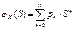устанавливается взаимноодноз-начное соответствие. Замечание 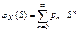– вероятностная производящая функция. В математике рассматриваются произвольные производящие функции. a₀, a₁ ,a₂... a₀ +Sa₁ +S²a₂ +… – производящая функция, если она имеет не нулевой радиус сходимости. Замечание 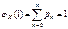Возьмем первую производную по S от производящей функции. 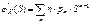,подставим значение S = 1. 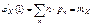.Возьмем вторую производную по S от производящей функции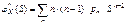 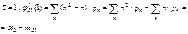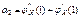. . 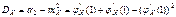. 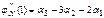То есть можно выразить начальные моменты более высокого порядка, через начальные моменты более низкого порядка. 23 Интегральная предельная теорема Муавра-Лапласа Теорема. При 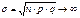равномерно по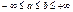 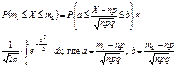Замечание. 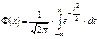– затабулирована. Ее значения приводятся только для 0£ x£3,5. Ф(–x)=1– Ф(x) Пример.Вероятность изделию некоторого производства оказаться бракованным равна 0,005 (p = 0,005).Чему равна вероятность, что из n = 10000 наудачу взятых изделий, бракованных окажется не более 70 (m = 70). 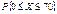– ?     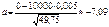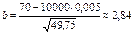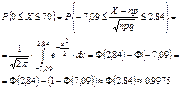24.Геометрическое распределение Опр.СВДТ Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, …, m, …, а вероятности этих значений 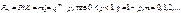Комментарий Вероятности P_m для последовательных значений m образуют геометрическую прогрессию с первым членом p и знаменателем q.На практике геометрическое распределение появляется в следующих условиях. Пусть производится ряд независимых испытаний (опытов) с целью получения какого-то результата (“успеха”) А. При каждом опыте “успех” достигается с вероятностью p. СВ Х – это число безуспешных опытов до первой попытки, в которой появляется результат А. Ряд распределения имеет следующий вид. X 0 1 2 … m …. P p qp q²p ... q^mp … Найдем числовые характеристики СВ Х распределенной по геометрическому закону.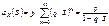 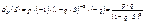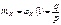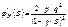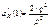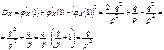; m_X=q/p ; ; 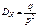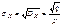На практике чаще приходится рассматривать не СВ Х, имеющую геометрическое распределение, а Y=X+1 – это число попыток до первого успеха, включая удавшуюся.Ряд распределения Y 1 2 … m …. P p qp … q^m–1p … –геометрическое распределение,сдвинутое на 1 (геометрическое плюс1). m_Y=M[X+1]=M[X]+1=q/p+1=1/p D_Y=D[X+1]=D[X]=q/p² 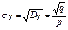25. Равномерное распределение Опр. СВНТ Х называется распределенной равномерно на [a,b], если f_X(x)=0 (при xÏ[a,b]) f_X(x)=C (при xÎ[a,b]), X~R(a,b). Найдем константу С. 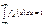; ; 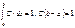C=1/(b–a).  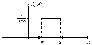 Пример.Шкала измерительного прибора проградуированных в некоторых единицах. СВ Х – ошибка при округлении отсчета до ближайшего целого деления, то она будет иметь равномерное распределение на (-1/2 ; 1/2).Найдем m_X, D_X, s_X – ? Решение.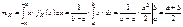 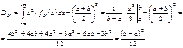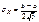Замечание. Моды равномерное распределение не имеет, а медиана совпадает с МО. h_X=m_X =(a+b)/2. Найдем функцию распределения и построим ее график. F_X(x)=P{X<x}  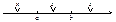 1)Случай 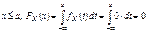. 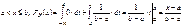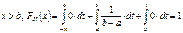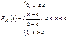2)Случай 3)Случай   29. Совместная функция распределения Пусть на одном и том же вероятностном пространстве (W,A,P) задано n СВ, 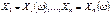, совокупность 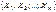– называется многомерной (n-мерной) СВ или случайным вектором. Совместная функция распределения:Рассмотрим в одном и том же вероятностном пространстве (W,A,P) набор СВ 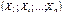. Так как множество 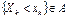, таких пересечения 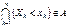, поэтому существует вероятность этого события, которая называется многомерной функцией распределения. 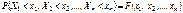Замечания:1.В дальнейшем ограничимся случаем двух случайных величин 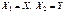. 2. Функция 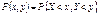– вероятность того, что случайная точка 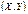попадает в бесконечный квадрант с вершиной в точке 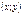. 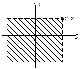С помощью F, можно вычислить вероятность попадания случайной точки в полуполосу или в прямоугольник. 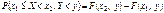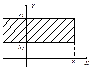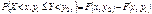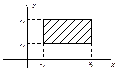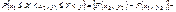а) б)   в)   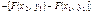Свойства. 1. 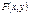по каждому аргументу не убывает и непрерывна слева. 2. 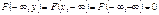. 3. 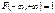. 4. а) При 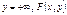становится функцией распределения компоненты x. 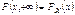. б) При 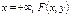становится функцией распределения компоненты y. 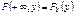.     34. Мультипликативные свойства математических ожиданий, аддитивное свойство дисперсии Теорема. Если СВ X и Y независимы, то M[XY]=M[X]*M[Y]. 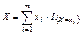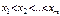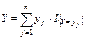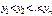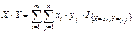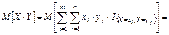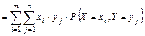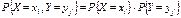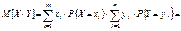Доказательство: Ограничимся случаем двух дискретных СВ принимающих конечное множество значений, тогда В силу аддитивности МО, Так как СВ независимы, то 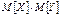g. Следствие: Если СВ 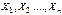– независимы, то 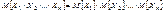(доказательство проводится методом математической индукции). Из мультипликативного СВ МО Þ аддитивное свойство дисперсии. Теорема. Если СВ X и Y независимы, то D[X+Y]=D[X]+D[Y]. Доказательство: D[X+Y]=M[((X+Y)–(m_X – m_Y))²]= M[((X– m_X)+( Y – m_Y))²]= M[(X– m_X)²+ 2(X– m_X)( Y – m_Y)+ (Y – m_Y)²]= D_X+D_Y+2 M[(X– m_X)(Y – m_Y)] Так как X и Y независимы, то X– m_X и Y – m_Y независимыÞ D[X+Y]=D_X+D_Y+2 M[(X– m_X)(Y – m_Y)], где X– m_X=M_X – m_X=0 и M_Y – m_Y=0 Þ D[X+Y]= D_X+D_Y g.Следствие: Если СВ X₁, X₂ ,..,X_n – независимы, то 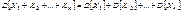37. Условное МО . Регрессия.Опр. Условным математическим ожиданием одной из СВ входящих в систему (X; Y) называется ее МО вычисленное при условии, что другая СВ приняла определенное значение. Замечание. То есть МО найденное на основе условного закона распределения. Если СВ 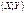дискретные, то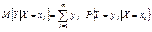 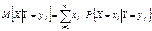Если СВ X и Y непрерывные, то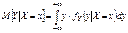 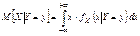Опр M[YïX=x]=j(x) называется регрессией Y на x. M[XïY=y]=y(y) называется регрессией X на y. Графики этих зависимостей от x и от y называются линиями регрессии или кривыми регрессии.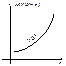 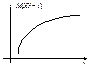Замечание. Для независимых СВ линии регрессии Y на x и X на y параллельны координатным осям так как МО каждой из них не зависит от того, какое значение приняла другая. Линии регрессии могут быть параллельны координатным осям и для зависимых СВ, когда МО каждой из них зависит от того, какое значение приняла другая. Так как все моменты начальные и центральные любых порядков представляют собой МО, то можно говорить об условных моментах. Например об условных дисперсияхD[YïX=x], D[XïY=y],.   38.Двумерные нормальные распределения. Опр.Нормальным законом распределения на плоскости называется распределение вероятностей двумерной СВ (X, Y), если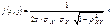 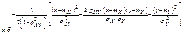Итак,нормальный закон на плоскости определяется 5-ю параметрами: m_X; m_Y; s_Y; s_Y; r_XY . Убедимся в том, что если компоненты X и Y не коррелированны, то они тогда и не зависимы. 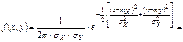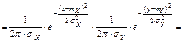r_XY=0 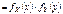Замечание: Для нормально распределенных компонент двумерной СВ понятие независимости и некоррелированности равносильны. Найдем условные законы распределения СВ X и Y воспользовавшись формулами.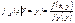   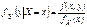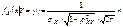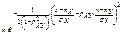. . 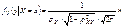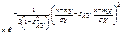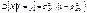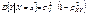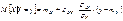Как легко видеть, каждый из условных законов распределения является также нормальных с условным МО и условной дисперсией вычисляемым по формуле: 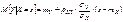Замечание. Из двух формул для условного МО видно, что для системы нормально распределенных X и Y, линии регрессии Y на x и X на y представляют собой прямые линии, то есть регрессия всегда линейна. В геометрической интерпретации график линейной формулы плотности представляет собой холмообразную поверхность.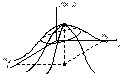 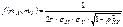.   Сечение поверхности 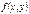плоскостями параллельными плоскости XOY представляют собой эллипсы.   41.Распределение c². (“хи-квадрат”). Пусть Z_i ~N(0;1) , i=1,2…k, тогда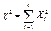 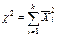–называется СВ распределенной по закону c² с k степенями свободны.    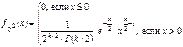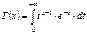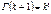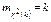 , 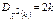. Распределение c² определяется одним параметром числом степеней свободы. С увеличением степеней свободы распределение c² медленно приближается к нормальному. На практике при k > 30 считают, что 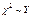, где 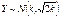.Для СВ, имеющей c² распределение существуют таблицы квантилей. 43. Распределение Фишера.Если U и V независимые СВ, распределенные по закону c², 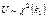, , 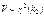тогда 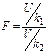имеет распределение, которое называется F–распределением или распределением Фишера со степенями свободы k₁ и k₂. 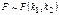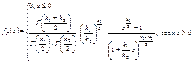( 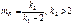F–распределение определяется двумя параметрами k₁ и k₂ и существует таблица квантилей. 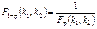.  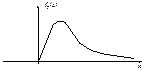 44. Неравенства Чебышева. Следующие два неравенства называют неравенствами Чебышева. Сформулируем их в виде теорем. Теорема: "x>0 имеют место неравенства: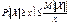 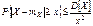. 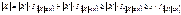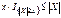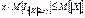Доказательство: Разложим ïXï в сумму двух слагаемых 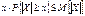, так как x > 0, получаем 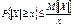. 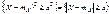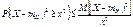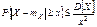g. Замечание. Очень часто второе неравенство Чебышева дают в такой форме 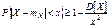. Второе неравенство Чебышева показывает, что при малой дисперсии с вероятностью близкой к 1 СВ Х концентрируется около своего МО.   48.Статистическое описание и вычисление оценок параметров распределения системы двух СВ. Пусть исход некоторого эксперимента описывается двумя СВ (X; Y).Предварительное представление о зависимости между X и Y можно получить, нанося элементы двумерной выборки (x_i , y_i ) , i=1,..,n, в виде точек на плоскость с выбранной системой координат. Такое представление называется диаграммой рассеяния. Опр. Распределением двумерной выборки называется распределение двумерного дискретного СВ случайного вектора, принимающего значения (x_i,, y_i) с вероятностями 1/n. Выборочные числовые характеристики вычисляются как соответствующие числовые характеристики двумерного дискретного случайного вектора. Если объем выборки небольшой, то тогда вычисления проводятся в следующей последовательности: 1. 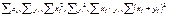. Контроль 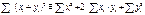. 2. Суммы квадратов отклонений от среднего и произведения отклонений от среднего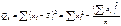  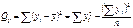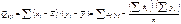 . 3. 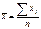; ; 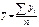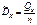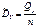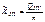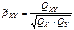. 49. Линии регрессии Для СВ X и Y. Регрессией Y на X называется условное МО 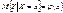. 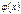используется для предсказания значения СВ Y по фиксированному значению СВ X. Если 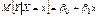, то говорят о линейной регрессии Y на X. 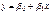– прямая регрессии. Оценки параметров линейной регрессии по выборке (x_i , y_i ) , i=1,..,n можно получить, используя МНК из условия минимума суммы 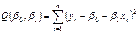. 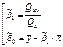–выборочные коэффициенты регрессии. 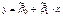; 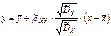. Выборочная линейная регрессия Y на X. Аналогично рассматривается X на Y. 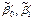; ; 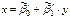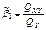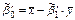. 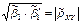Обе прямые регрессий пересекаются в точке с координатами 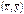. Угол между этими двумя прямыми уменьшается при увеличении коэффициента корреляции. При 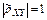обе прямые совпадают. Замечание Прямые 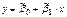и 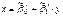должны быть различны.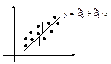     52. Интервальные оценки. Доверительный интервал. Доверительная вероятность. В ряде задач требуется не только найти для параметра 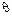подходящую оценку 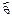, но и указать к каким ошибкам может привести замена параметра 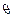его оценкой 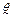, т.е. требуется оценить точность и надежность оценки. Для определения точности оценки 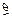в статистике пользуются доверительными интервалами. Для определения надежности оценки 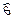в статистике пользуются доверительной вероятностью. Опр. Доверительным интервалом для параметра 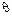называется интервал 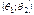, содержащий истинное значение параметра с заданной вероятностью 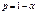. . 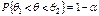Опр. Число 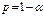называется доверительной вероятностью, а значение a – уровнем значимости. Замечание. Нижняя 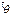и верхняя 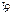граница доверительного интервала определяется по результатам наблюдений и следовательно является СВ. Поэтому так и говорят, что доверительный интервал «накрывает» оцениваемый параметр с вероятностью 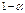. Выбор доверительной вероятности каждый раз определяется конкретной постановкой задачи. Обычно р = 0,9; р = 0,95; р = 0,99. Часто применяют односторонние доверительные интервалы 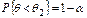(левосторонний), 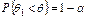(правосторонний). В простейших случаях метод построения доверительных интервалов состоит в следующем 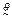–оценка 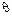, 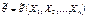. Предположим, что существует непрерывная и монотонная функция Y, зависящая от 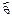и 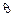, но такая, что ее распределение не зависит от 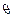и других параметров. Для нахождения границ доверительного интервала 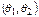по заданной доверительной вероятности 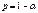. В этом случае можно использовать неравенство 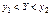, где числа 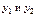, определяются из условия 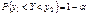Рассмотрим нахождение доверительного интервала для среднего и дисперсии нормально распределенной генеральной совокупности.   53. Доверительный интервал для оценки МО при известной дисперсии 1) Доверительный интервал для оценки МО при известной дисперсии нормально распределенной генеральной совокупности. Пусть 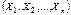– выборочный вектор n–наблюдений СВ Х, где 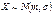. В качестве оценки для m возьмем 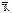. Предположим, что 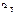известна. Рассмотрим статистику 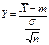. Статистика 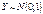. По таблице нормального распределения найдем квантил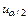и и 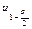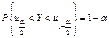. . 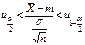. . 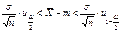. 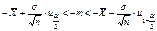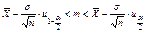Учитывая, что 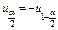получаем 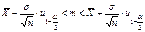.   57. Критерий 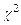и его применение. Критерий 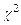применяется в частности для проверки гипотез о виде распределения генеральной совокупности. Процедура применения критерия 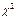для проверки гипотезы H₀, утверждающей, что СВ Х имеет закон распределения 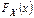состоит из следующих этапов. Этапы: 1. По выборке найти оценки неизвестных параметров предполагаемого закона 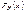. 2. Если Х–СВДТ – определить частоты 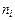, i = 1, 2, …, r, с которым каждое значение встречается в выборке. Если Х–СВНТ – разбить множество значений на r – непересекающихся интервалов 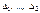и попавших в каждый из этих интервалов 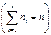. 3. Х–СВДТ вычислить 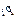. Х–СВНТ вычислить 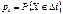. 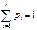4. 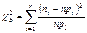. 5. Принять статистическое решение. 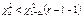– гипотеза Н₀ – принимается. 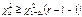– гипотеза Н₀ – отклоняется. e – количество оцениваемых параметров. Малочисленные частоты надо будет объединять. Проверка гипотезы о равномерном распределении генеральной совокупности. n = 200 А;    

№	(xi-1, xi)	ni
	2 – 4		a =0,05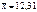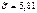
	4 – 6
	6 – 8
	8 – 10
	10 – 12
	12 – 14
	14 – 16
	16 – 18
	18 – 20
	20 – 22

1.

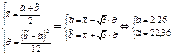
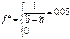
2.

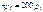
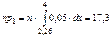
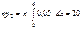
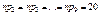
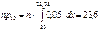
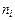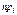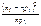	17,3	0,79
		0,8

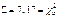
k = 10 – 2 – 1 = 7

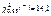
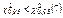– нет основания отвергать гипотезу о том, что выборка взята из генеральной совокупности и имеет равномерное распределение.