Правильные области. Вычисление двойного интеграла в декартовых координатах.
Производная по направлению и градиент функции n переменных. Связь между градиентом и
Производной по направлению. Координаты градиента.
8. Чистые и смешанные производные. Теорема о смешанных производных.
9. Дифференциалы второго и высших порядков функции n переменных. Общий вид второго
дифференциала.
10. Неявная функция n переменных, теорема о неявной функции, частные производные неявной
функции. Уравнения касательной плоскости и нормали в случае неявного задания поверхности.
Особые точки кривой и поверхности.
11. Экстремум функции n переменных. Необходимое условие экстремума.
12. Достаточное условие экстремума. Матрица Гессе, главные миноры, их использование при
проверке достаточного условия экстремума.
13. Определение условного экстремума. Два способа нахождения условного экстремума. Функция
Лагранжа и её использование при нахождении условного экстремума.
14. Формула Тэйлора функции n переменных.
15. Дифференциальные уравнения - основные определения.
16. Дифференциальные уравнения первого порядка – формы записи, теорема Коши, общее и
частное решения, начальные условия, задача Коши, общий и частный интегралы,
интегральные кривые. Особые решения.
17. Уравнения первого порядка, интегрируемые в квадратурах – с разделяющимися
Переменны ми, однородные уравнения первого порядка, линейные первого порядка и
уравнения Бернулли,уравнения в полных дифференциалах.
18. Дифференциальные уравнения высших порядков. Теорема Коши, общее и частное решения,
начальные условия.
19. Уравнения второго порядка, допускающие понижение порядка.
20. Линейные уравнения высших порядков, основные определения.
21. ЛОДУ n. Вронскиан, теорема о вронскиане.
Теорема о структуре общего решения ЛОДУ n. ФСР ЛОДУ.
ЛНДУ n, теорема о структуре общего решения ЛНДУ.
ЛОДУ n с постоянными коэффициентами. Характеристическое уравнение. Нахождение ФСР
В зависимости от вида корней характеристического уравнения.
25. ЛНДУ с постоянными коэффициентами. Нахождение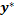 
методом Лагранжа.
26. Специальные правые части.Нахождение 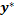методом подбора. Принцип суперпозиции
Решений.
27. Краевые задачи для дифференциальных уравнений. Отличие от задачи Коши.
28. Нормальные системы, общее и частное решения, интегральные кривые. Геометрическая
интерпретация . Фазовая траектория и фазовая плоскость. Автономные системы. Точки покоя.
29. ЛОС с постоянными коэффициентами, ФСР ЛОС, ФМС ЛОС, нормированная ФМС.
Отыскание общего решения с помощью ФСР и ФМС, частного решения с помощью
нормированной ФМС.
30. Методы решения ЛОС - сведение к одному уравнению, разделение ЛОС на подблоки,
с помощью матричной экспоненты.
31. ЛНС с постоянными коэффициентами, решение методом Лагранжа.
32. Понятие об устойчивости решения дифференциального уравнения и системы. Теорема о точках покоя ЛОС.
33. Двойной интеграл – определение, теорема существования, свойства, геометрический смысл.
Правильные области. Вычисление двойного интеграла в декартовых координатах.
35. Взаимно-однозначное соответствие между областями. Якобиан преобразования. Замена
переменных в двойном интеграле. Переход в двойном интеграле к полярным координатам.
36. Применение двойного интеграла – площадь плоской области, площадь поверхности, объем
цилиндрического бруса, механические приложения.
37. Тройной интеграл, вычисление в правильной области, замена переменных. Цилиндрическая и
сферическая системы координат, их якобианы.
38. Поверхностный интеграл 1-го рода, вычисление в декартовых координатах.
39. Поток векторного поля, вычисление в декартовых координатах.
40. Дифференциальные характеристики векторного поля – ротор и дивергенция, вычисление в
декартовых координатах. Дифференциальные операции второго порядка.
41. Теоремы Гаусса-Остроградского, Стокса, Грина.
42. Специальные виды векторных полей – потенциальное, соленоидальное, гармоническое.
Потенциал потенциального поля, восстановление потенциала. Теорема о потенциале
гармонического поля.
Чёрным шрифтом выделены вопросы на тройку.