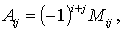Свойства определителей. Прямоугольная матрица

Прямоугольная матрица

Назовём матрицей размера 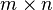(читается на ) количество строк и столбцов не совпадает.

9. определитель характеризует содержание матрицы(только для квадратных).

Свойства определителей

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами.СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,

.

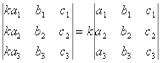СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

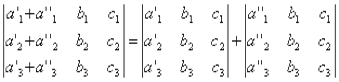
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится.Минором 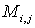элемента 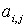матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца. Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца: