Закон Ома в дифференциальной форме
Электрическое поле в проводящей среде
Ток и плотность тока проводимости
Если в проводящей среде (металлических проводниках, земле, жидких проводниках) создано электрическое поле, оно вызывает упорядоченное движение зарядов, представляющих собой ток проводимости. В металлах ток проводимости определяется движением свободных электронов. Мерой тока служит предел отношения заряда Δq, проходящего сквозь заданную поверхность в течение некоторого времени Δt, к величине Δt, когда Δt стремится к нулю:
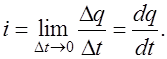
Ток – величина скалярная. Если значение тока не зависит от времени, ток называется постоянным. Векторную величину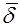 
,численно равную пределу отношения тока, протекающего через некоторую площадку, расположенную нормально к направлению движения зарядов, к величине площади этой площадки, при ее стремлении к нулю называют плотностью тока:
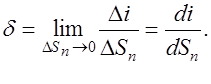
Направление вектора 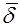выбирается таким образом, чтобы оно совпадало с направлением движения положительных зарядов. Ток и плотность тока связаны соотношением
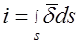 | (42.1) |
Ток сквозь поверхность S равен потоку вектора плотности тока сквозь ту же поверхность. Плотность тока измеряется в амперах на квадратный метр (А/м2).
Закон Ома в дифференциальной форме
Выделим в проводящей среде небольшой параллелепипед объемом ΔV. Длина ребра параллелепипеда Δl, площадь поперечного сечения ΔS. Расположим этот параллелепипед так, чтобы напряженность поля в нем была направлена параллельно ребру (рис.42.1).
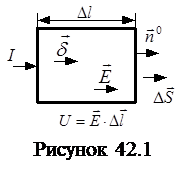В силу малости объема можно считать, что напряженность электрического поля одна и та же во всем элементарном объеме;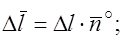 
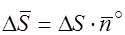, где 
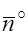– единичный вектор по направлению 
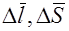и 
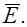Ток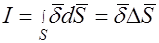 
. Напряжение на элементе объема 
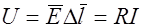. Сопротивление элемента объема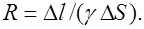 
Подставив в выражение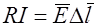 
эквиваленты R и I, получим
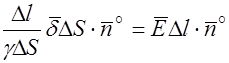, откуда
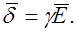 | (42.2) |
Соотношение (42.2) называют законом Ома в дифференциальной форме. Оно устанавливает связь между плотностью тока в данной точке проводящей среды и напряженностью поля в этой же точке.
Для того чтобы в проводнике непрерывно существовал ток, необходимо наличие электрического поля, силы которого перемещают электрические заряды. Такое поле создается и поддерживается процессами неэлектростатического происхождения (химическими, термоэлектрическими и др.) и носит название стороннего электрического поля.
Так как при прохождении тока по проводнику все время происходит преобразование электрической энергии в тепловую, энергия поля должна непрерывно пополняться за счет внешнего источника. Только при этом условии может длительно существовать ток.
Следовательно, стороннее поле всегда связано с источником энергии, который преобразует какую-либо форму энергии (тепловую, химическую, механическую) в энергию электрическую и поддерживает ток в проводнике.
Напряженность стороннего поля обозначают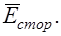 
Если на заряд q в проводнике действует сторонняя сила Fстор, то
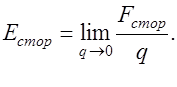
Если в проводнике одновременно действуют и электростатические и сторонние силы, напряженность электрического поля равна:
Eрез = Е+Естор.
Закон Ома в дифференциальной форме для областей, занятых источниками ЭДС, записывают следующим образом:
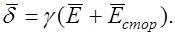 | (42.3) |
3. Закон Джоуля – Ленца в дифференциальной форме
Мощность тепловых потерь в проводнике равна произведению тока и напряжения P = IU.
Если рассмотреть в проводящей среде элемент объема dV, то мощность тепловых потерь
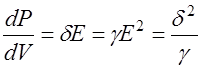 | (42.4) |
Формула (42.4) является дифференциальной формой закона Джоуля – Ленца. Мощность тепловых потерь в объеме V можно выразить следующим образом:
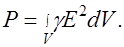 | (42.5) |