Вычисление обратной матрицы

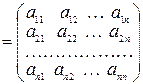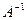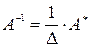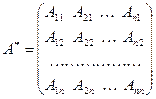Теорема. Пусть A – неособенная матрица, т.е. D=detA≠0. Тогда существует матрица - обратная к A, причем , где (матрица из алгебраических дополнений к элементам A, транспонированная).

Доказательство.

Достаточно проверить выполнение равенства 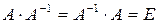. Но

,

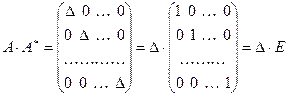т.к.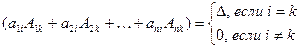

.

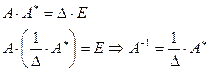
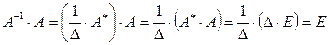Теорема доказана.

Вычисление ранга матрицы

Теорема. Ранг матрицы равен наибольшему порядку ее ненулевых миноров.

Доказательство.

Пусть A - произвольная матрица размера m´n и r=rangA. Сформулируем теорему в виде критерия: r=rangA тогда и только тогда, когда у матрицы A есть ненулевой минор r порядка, а все миноры, порядка больше чем r, нулевые.

Необходимость. Пусть r=rangA, то есть в A имеется система из r линейно независимых строк. Образуем из них матрицу B. В матрице B имеется система из r линейно независимых столбцов, так как r=rangB. Из этих столбцов составим матрицу C, которая будет квадратной порядка r и ранга r, то есть она является неособенной и поэтому detC¹0. А определитель матрицы C является минором r-го порядка матрицы A. Следовательно, существует ненулевой минор r - порядка матрицы A.

Пусть s>r. Образуем матрицу D из s произвольно выбранных строк матрицы A, причем среди них не обязательно окажется система из r линейно независимых строк и поэтому r₁=rangD£r. Из s произвольно выбранных столбцов матрицы D составим матрицу G, причем среди них не обязательно окажется система из r₁ линейно независимых столбцов матрицы D, то r₂=rangG£r₁. :G- квадратная матрица порядка s ранга r₂<s. G является особенной матрицей и поэтому detG=0. Определитель G является произвольным минором порядка s матрицы A. Следовательно, все миноры матрицы A порядка s>r нулевые.

Достаточность. Пусть у матрицы A есть ненулевой минор r порядка, а все миноры, порядка больше чем r, нулевые. Предположим, что ранг матрицы A равен s.

Если бы s<r, то по ранее доказанному имеем: любой минор порядка большего чем s нулевой, а значит и любой минор порядка r нулевой. Противоречие.

Если бы s>r, то по ранее доказанному имеем: существует ненулевой минор r-го порядка. Противоречие.

Следовательно, остается принять, что rangA=r. Теорема доказана.

Пример.

Вычислить ранг матрицы

.

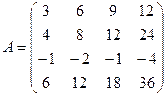Решение. Используем метод окаймляющих миноров, основанный на том, что ранг данной матрицы равен порядку такого минора данной матрицы, который отличен от нуля, а все его окаймляющие миноры равны нулю.

I.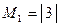

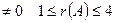
II.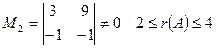

III.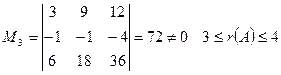

IV. .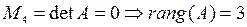

Теорема Бине-Коши

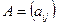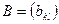Теорема. Пусть и - матрицы размером 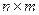и 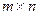соответственно, и пусть 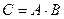. Тогда:

.

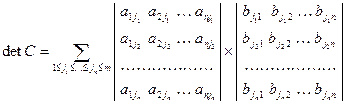Суммирование в правой части проходит по всем 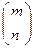возможным комбинациям по n элементов 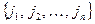из 1, 2, …, m. В частности, при m=n и 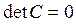при n>m.

Для доказательства необходимо отметить, что так как 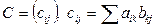, то:

,

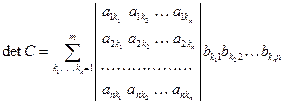где суммирование происходит по всем попарно различным 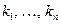. При m<n таких индексов нет, и, следовательно, 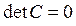. Если же 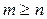, то 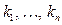- выборка элементов 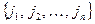, взятых в каком-то порядке из 1, 2, …, m. Следует собрать все члены, соответствующие фиксированной комбинации 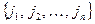, и получить нужное выражение:

,

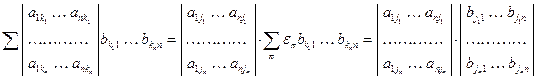где .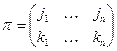

Теорема Лапласа

Данному минору 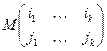порядка k для 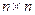-матрицы 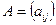отвечает дополнительный минор 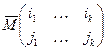порядка n-k, матрица которого получается из A вычеркиванием строк с номерами 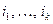и столбцов с номерами 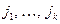. Выражение:

,

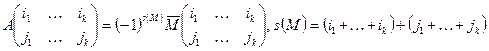называется алгебраическим дополнением к 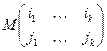. При k=n-1 мы приходим к обычному определению алгебраического дополнения. При последовательном разложении определителя по элементам строк с номерами 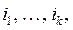справедлива следующая теорема:

Теорема Лапласа. Пусть в матрице 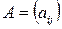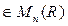выбраны k строк с номерами 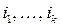. Тогда:

.

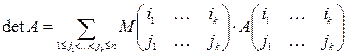При произвольном n теорема Лапласа известна в двух частных случаях: 1) k=1; 2) A – матрица с углом нулей размера .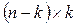

Случай теоремы Лапласа для :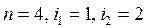

.

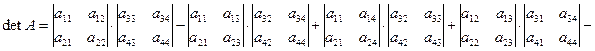
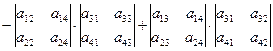Упражнения

30. Вычислить определители:

a) ;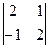

b) ;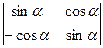

c) ;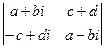

d) ;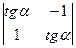

e) ;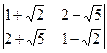

f) ;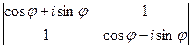

g) ;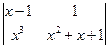

h) 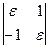, где .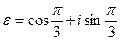

31. Вычислить определители:

a) ;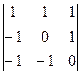

b) ;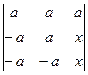

c) ,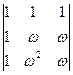

где .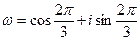

32. С каким знаком в определитель 6-ого порядка входят произведения:

a) ;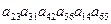

b) ?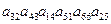

33. Входят ли в определитель 5-ого порядка произведения:

a) ;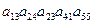

b) ?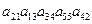

34. Почему следующий определитель равен нулю?

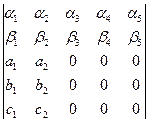
35. Вычислить определители:

a) ;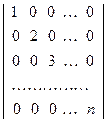

b) .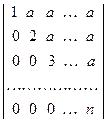

36. Доказать, что определитель нечетного порядка равен 0, если все элементы его удовлетворяют условию: 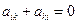(кососимметрический определитель).

37. Определитель 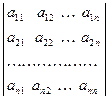равен D. Чему равен определитель ?

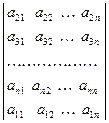38. Числа 204, 527, 255 делятся на 17. Доказать, не вычисляя определитель, что 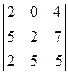делится на 17.

39. Вычислить определители, разложив их по элементам строки (столбца), содержащей буквы:

a) ;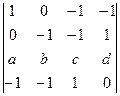

b) ;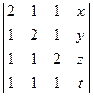

c) .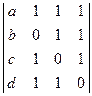

40. Доказать, что:

.

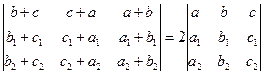41. Упростить определитель 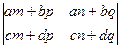, разложив его на слагаемые.

42. Вычислить определители:

a) ;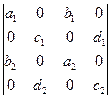

b) .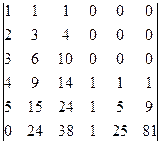

43. Написать разложение определителя четвертого порядка по минорам первых двух строк.

44. Пусть A, B, C, D – определители третьего порядка, составленные из матрицы 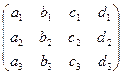вычеркиванием соответственно первого, второго, третьего и четвертого столбцов. Доказать, что:

.

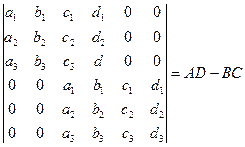45. Вычислить определители:

a) ;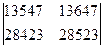

b) ;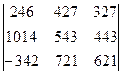

c) ;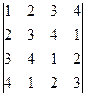

d) ;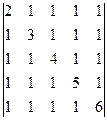

e) ;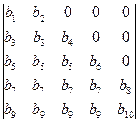

f) ;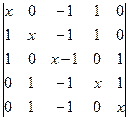

g) ;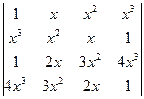

h) ;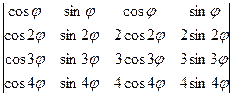

i) ;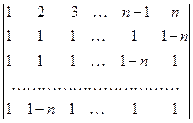

j) ;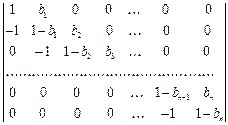

k) ;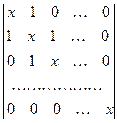

l) ;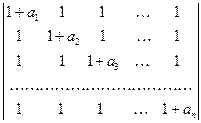

m) ;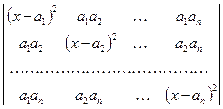

n) ;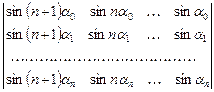

o) .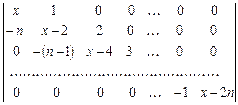

46. Решить методом Крамера:

a) ;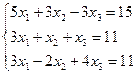

b) ;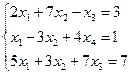

c) ;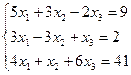

d) ;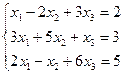

e) ;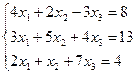

f) ;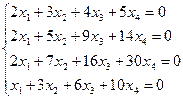

g) ;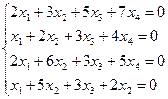

h) ;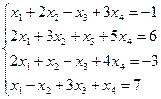

i) ;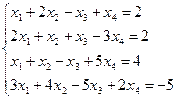

j) .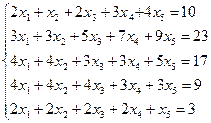

47. Решить системы линейных уравнений матричным способом, при этом обратную матрицу вычислить с помощью определителей.

a) ;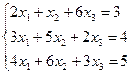

b) ;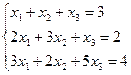

c) ;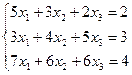

d) ;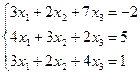

e) ;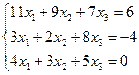

f) .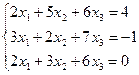

Варианты контрольных заданий

Вариант 1 («Прикладная математика», контрольная №1).

1. Вычислить .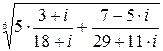

2. Исследовать систему линейных уравнений с параметром методом Гаусса:

.

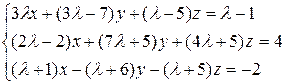3. Исследовать систему векторов на линейную зависимость, ранг и базис:

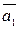=(2, 4, 6, 0, 8), 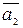=(3, 3, -1, 2, 5), 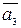=(5, -4, -2, -1, -3), 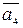=(13, 1, 5, 7, -4).

4. Найти общее решение и ФСР однородной системы линейных уравнений:

.

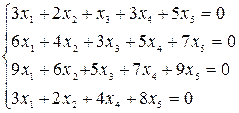Вариант 2 («Прикладная математика», контрольная №2).

1. Методом Крамера решить систему линейных уравнений:

.

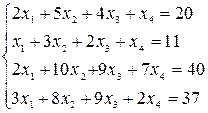2. Матричным методом решить систему линейных уравнений (обратную матрицу найти с помощью определителей):

.

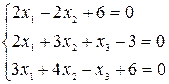3. Вычислить определитель

.

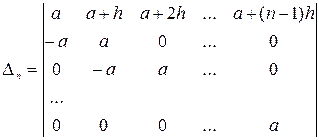Вариант 3 («Программное обеспечение вычислительной техники», контрольная №1).

1. Вычислить .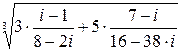

2. Исследовать систему векторов на линейную зависимость, ранг и базис:

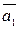=(0, 1, -3, 2, -4), 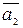=(5, -1, -2, 3, -1), 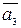=(-2, -3, 1, -4, 7),
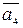=(3, -2, -7, 3, -2).

3. Методом Крамера решить систему линейных уравнений:

.

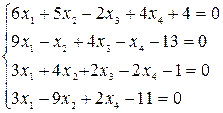4. Матричным методом решить систему линейных уравнений (обратную матрицу найти с помощью определителей):

.

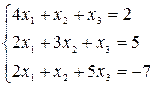Литература

1. Дадаян А.А. Алгебра и геометрия / А.А. Дудаян, В.А. Дударенко. Минск: Высш. шк., 1989. 190 с.

2. Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. М.: ФИЗМАТЛИТ, 2001. 160 с.

3. Фаддеев Д.К. Сборник задач по высшей алгебре / Д.К. Фаддеев, И.С. Соминский. М.: Наука, 1996. 200 с.

4. Кострикин А.И. Введение в алгебру. Основы алгебры: Учебник для вузов. М.:ФИЗМАТЛИТ, 1994. 320 с.

5. Сборник задач по алгебре: Учеб. пособие / Под ред. А.И. Кострикина. М.: Факториал, 1995. 454 с.

6. Кантор И.Л. Гиперкомплексные числа / И.Л. Кантор, А.С. Солодовников. М.: Наука, 1973. 144 с.

7. Ланкастер П. Теория матриц. М.: Наука, 1982. 272 с.