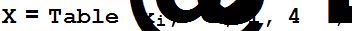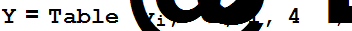Находим перпендикуляр из вектора f на линейную оболочку заданных векторов

h=f-g

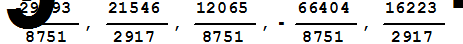
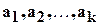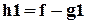Можно доказать, что если - произвольный вектор, принадлежащий линейной оболочке векторов { } , , то выполняется соотношение

.

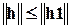Пусть система (3.1) несовместна. Это означает, что нельзя найти такие числа 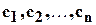, что при подстановке этих чисел вместо неизвестных 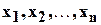удовлетворялись бы все уравнения системы. Если подставить какие-нибудь числа 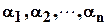вместо неизвестных 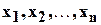в левые части уравнений рассматриваемой системы, то мы получим результаты 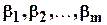, отличные от данных величин .

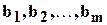В этом случае ставится следующая задача: определить числа 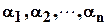так, чтобы квадратичное уклонение результатов 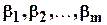от данных величин 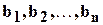, определяемое соотношением

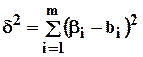
Оказалось наименьшим из всех возможных, а так же найти это минимальное уклонение.

Рассмотрим векторов 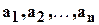, компоненты которых выписаны в столбцах системы (3.1):

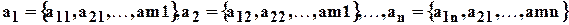
Составляя линейную комбинацию

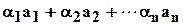
Мы получим вектор 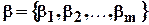. Нужно определить числа 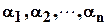таким образом, чтобы вектор по норме имел наименьшее возможное отклонение от вектора 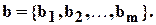В силу сказанного выше, это будет в том случае, если вектор мы положим равным проекции вектора 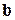на линейную оболочку векторов .

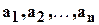Рассмотрим следующий пример. Найти методом наименьших квадратов решение следующей системы линейных уравнений.

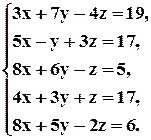
Полагаем

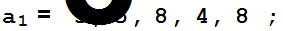
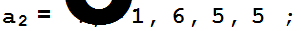
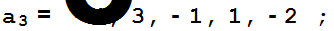
b={19,17,5,17,6};

Строим матрицу A и вектор B

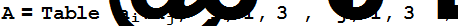
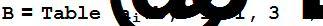
Находим решение заданной системы линейных уравнений методом наименьших квадратов

R=LinearSolve[A,B]

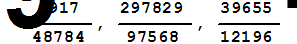
Отметим, что при использовании системы Mathematica нам безразлично, является ли система векторов 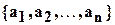линейно зависимой или нет.

Квадратичные формы.

Пусть 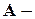симметричная матрица порядка . Квадратичной формой от переменных называется функция следующего вида

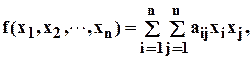(4.1)

где 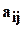-элементы матрицы 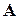. Матрица 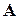называется матрицей квадратичной формы. Ранг матрицы 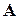называется рангом квадратичной формы.

Пусть 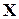-вектор с компонентами 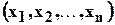. Тогда в системе Mathematica квадратичная форма (4.1) может быть записана следующим образом 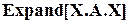. Рассмотрим следующий пример.

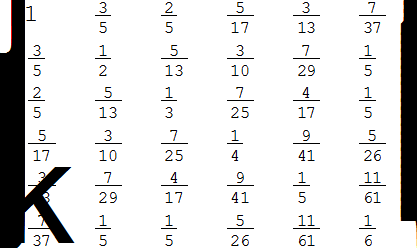
A=Table[(i+j)/(i^2+j^2),{i,1,6},{j,1,6}];

MatrixForm[A]

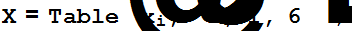
f=Expand[X.A.X]

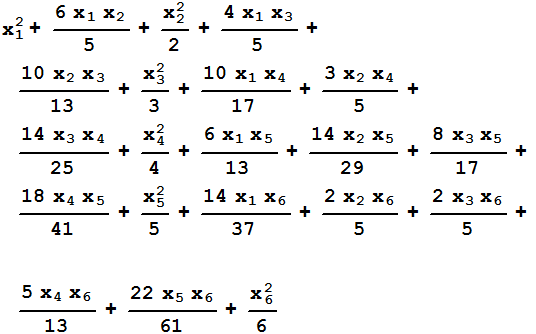
Квадратичная форма называется положительно определённой, если для любого ненулевого вектора её значения положительны. Можно доказать, что квадратичная форма тогда и только тогда является положительно определённой, когда все собственные числа матрицы этой квадратичной формы положительны. В нашем примере

Следовательно, рассматриваемая квадратичная форма является положительно определённой.

Приведём ещё один критерий положительной определённости квадратичной формы, не связанный с необходимостью вычислять собственные числа матрицы.

Введём следующие обозначения. Пусть 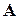- матрица квадратичной формы. Рассмотрим угловые миноры этой матрицы (которые называют также главными минорами ):

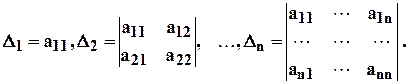(4.2)

Как мы видим, угловой минор порядка 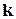расположен на пересечении первых 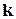строк и первых 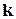столбцов матрицы. Угловой минор максимального 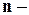го порядка представляет собой определитель матрицы.

Имеет место следующая теорема ( критерий Сильвестра ) : для того, чтобы квадратичная форма от переменных была положительно определена необходимо и достаточно, чтобы выполнялись неравенства

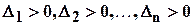. (4.3)

При помощи этого критерия исследуем рассмотренную ранее квадратичную форму.

<< LinearAlgebra`MatrixManipulation`

A=Table[(i+j)/(i^2+j^2),{i,1,6},{j,1,6}];

D=Table[Det[SubMatrix[A,{1,1},{k,k}]],{k,1,6}]

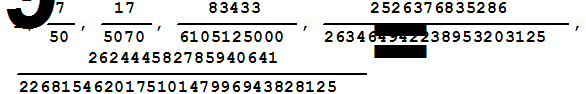
Следовательно, рассматриваемая квадратичная форма положительно определена.

Применим к квадратичной форме (4.1) невырожденное линейное преобразование переменных

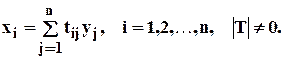(4.4)

Мы получим новую квадратичную форму

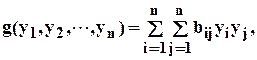(4.5)

матрица которой может быть найдена из матрицы исходной квадратичной формы следующим образом

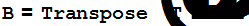
Две квадратичные формы, получающиеся одна из другой невырожденным линейным преобразованием, называются эквивалентными.

Можно доказать, что две эквивалентные квадратичные формы имеют одинаковый ранг.

Квадратичная форма называется канонической, если она не содержит произведений переменных, т.е. имеет вид

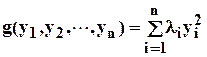. (4.6)

Некоторые из коэффициентов 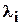могут равняться нулю. Если формы (4.1) и (4.6) эквивалентны, то форма (4.6) называется каноническим видом формы (4.1). Любую квадратичную форму при помощи невырожденного линейного преобразования можно привести к каноническому виду.

Пусть матрица квадратичной формы (4.1) имеет ранг 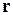и все её угловые миноры от первого до 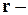го отличны от нуля. Опишем метод приведения такой формы к каноническому виду, предложенный немецким математиком К.Якоби.

Приведём матрицу 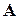к треугольному виду, в котором все строки, начиная с 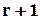равны нулю. В последних 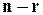строках главной диагонали поставим единицы, а остальные элементы оставим равными нулю. Найдём матрицу, обратную полученной. Обозначим эту матрицу через 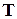. Это и будет матрица невырожденного преобразования, приводящего заданную квадратичную форму к каноническому виду.

Пример. Найти канонический вид и соответствующее невырожденное линейное преобразование переменных для квадратичной формы

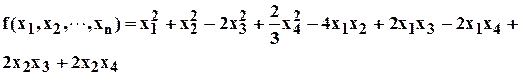
Решение.

Запишем матрицу A данной квадратичной формы и положим H=A

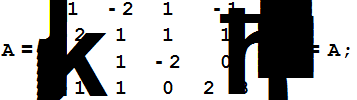
Приведём матрицу H к треугольному виду

H[[2]]=H[[2]]+2*H[[1]];

H[[3]]=H[[3]]-H[[1]];

H[[4]]=H[[4]]+H[[1]];

MatrixForm[H]

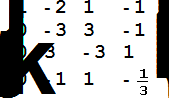
H[[3]]=H[[3]]+H[[2]];

H[[4]]=H[[4]]-H[[2]]/3;

MatrixForm[H]

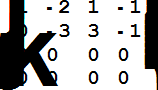
H[[3,3]]=1;H[[4,4]]=1;

T=Inverse[H];