Тема 2 Аналитическая геометрия на плоскости
Задача 1. Даны вершины треугольника АВС: А(-4;8), В(5;-4), С (10;6). Найти: 1)длину сторон АВ 2)уравнения сторон АВ и АС и их угловые коэффициенты; 3)внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и её длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
Решение: 1. Расстояние d между точками М1 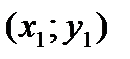 и М 2 (x2;y2) определяется по формуле:
и М 2 (x2;y2) определяется по формуле: 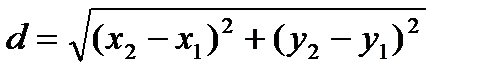 (1)
(1)
Подставив в эту формулу координаты точек А и В, имеем:
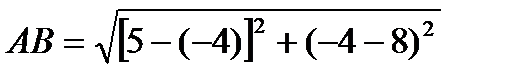 =
= 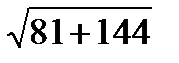 =15
=15
2. Уравнение прямой, проходящей через точки М1 (x1;y1) и М2(x2;y2), имеет вид: 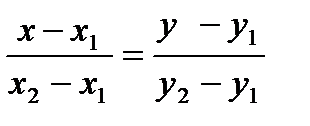 (2)
(2)
Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:
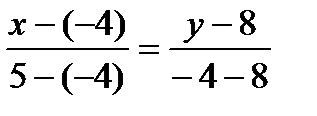 ,
, 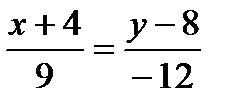 ,
, 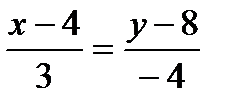
3y-24=-4x-16, 4x+3y-8=0 (AB)
Для нахождения углового коэффициента kАВ прямой АВ разрешим полученное уравнение относительно 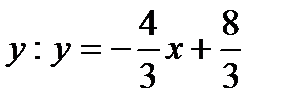 . Отсюда kАВ =
. Отсюда kАВ = 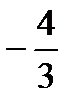 . Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС.
. Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС.
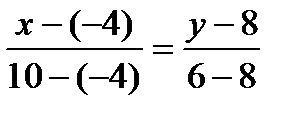 ,
, 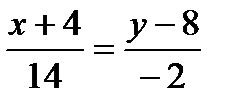 ,
, 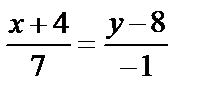 ,
,
x+7y-52=0 (АС). Отсюда kАС = 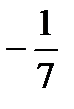
3. Угол 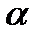 между двумя прямыми, угловые коэффициенты которых равны k1 и k2, определяется по формуле:
между двумя прямыми, угловые коэффициенты которых равны k1 и k2, определяется по формуле: 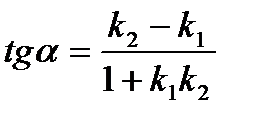 (3)
(3)
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее
k1= kАВ= 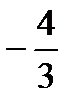 , k2 =kАС =
, k2 =kАС = 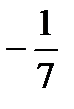 .
.
tg А 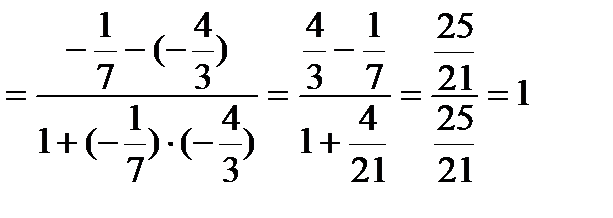 .
.
Итак, имеем 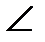 А=arctg1=450
А=arctg1=450 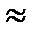 0.79 радиан.
0.79 радиан.
4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку:
kCD= 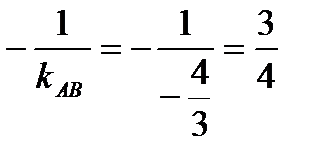 .
.
Уравнение прямой, проходящей через данную точку M1 (x1;y1) в заданном угловым коэффициентом k направлении, имеет вид: y - y1=k(x - x1). (4)
Подставив в (4) координаты точки С и kCD= 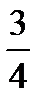 , получим уравнение высоты CD:
, получим уравнение высоты CD: 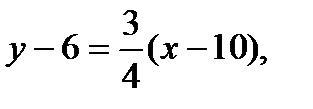
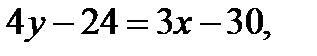
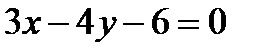 (CD). (5)
(CD). (5)
Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (CD):
4x+3y – 8=0,
3x – 4y – 6=0, откуда x=2, y=0, то есть D(2;0).
Подставив в формулу (1) координаты точек С и D, находим:

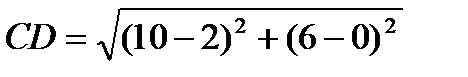
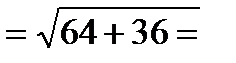 10.
10.
5. Уравнение окружности радиуса R с центром в точке Е(a;b) имеет вид:
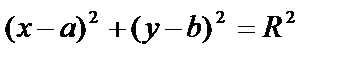 (6)
(6)
Так как CD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим:
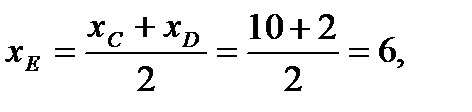
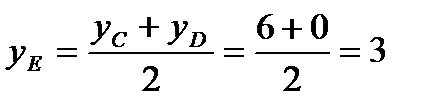 .
.
Следовательно, Е(6; 3) и R= 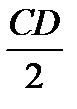 =5. Используя формулу (6), получаем уравнение искомой окружности: (х — 6) 2+(y — 3) 2 =25.
=5. Используя формулу (6), получаем уравнение искомой окружности: (х — 6) 2+(y — 3) 2 =25.
6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и со-держит точку А, а третья ограничена прямой АС, и содержит точку В.
Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С: 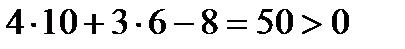 . Поэтому искомое неравенство, имеет вид:
. Поэтому искомое неравенство, имеет вид: 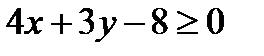 . Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:
. Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:
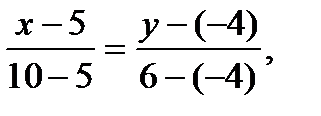
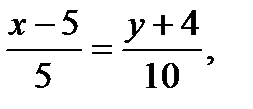
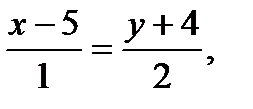 2x – y – 14=0 (BC)
2x – y – 14=0 (BC)
Подставив в последнее уравнение координаты точки А, имеем: 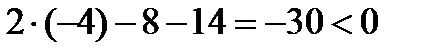 Искомое неравенство будет
Искомое неравенство будет 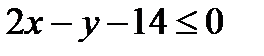 . Подобным образом составим неравенство, определяющее полуплоскость, orpaниченную прямой АС и содержащую точку В:
. Подобным образом составим неравенство, определяющее полуплоскость, orpaниченную прямой АС и содержащую точку В: 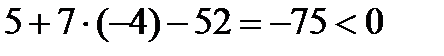 . Третье искомое неравенство
. Третье искомое неравенство 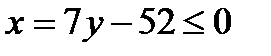 . Итак, множество точек треугольника АВС определяется системой, неравенств
. Итак, множество точек треугольника АВС определяется системой, неравенств
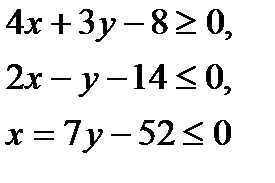
у
A(-4;8)
C(10;6)
E•
0 D x
B(5;-4)
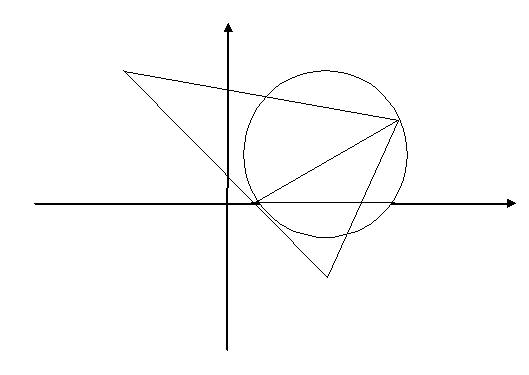
Рис.1
На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АВС, высота CD, окружность с центром в точке Е.
Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки A(3; 0) и до прямой х=12 равно числу 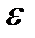 =0,5. Полученное уравнение привести к простейшему виду и построить кривую.
=0,5. Полученное уравнение привести к простейшему виду и построить кривую.
Решение. Пусть М(х; у) — текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр МВ на прямую х=12 (рис. 2). Тогда В (12; у).
По условию задачи 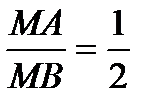 . По формуле (1) из предыдущей задачи
. По формуле (1) из предыдущей задачи
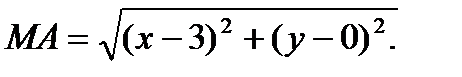
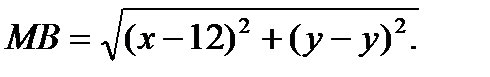
 Тогда
Тогда 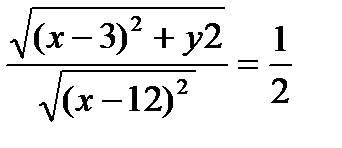 ,
,
4x2 – 24x+36+4y2 = x2– 24x +144, 3x2+4y2=108,
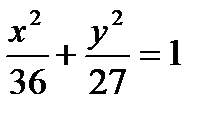
Полученное уравнение представляет собой эллипс вида 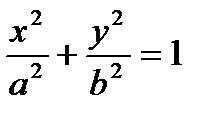 , где а = 6, b =
, где а = 6, b = 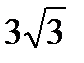 .
.
Определим фокусы эллипса F1( - с; 0) и F2 (c; 0). Для эллипса справедливо равенство b2 = a2 - c2 , откуда c2 = a2 - b2 = 9 и с = 3. То есть, F1 ( -3; 0) и F2 (3; 0) — фокусы эллипса (точки F и А совпадают). Эксцентриситет эллипса 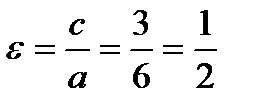
 у
у
М В
-3 0 A 3 6 12 x
Рис. 2
Задача 3. Составить ypaвнение линии, для каждой точки которой ее расстояние до точки А (3; — 4) равно расстоянию до прямой у=2. Полученное уравнение привести к простейшему виду и построить кривую.
Решение. М(х;у) — текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у = 2 (рис. 3). Тогда В (х; 2). Так как МА=МВ, то
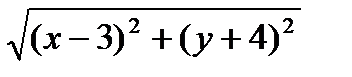
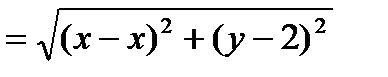 или
или
(x-3)2+y2+8y+16= y2-4y+4
-12y-12=(x-3) 2
y+1= 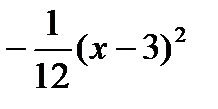
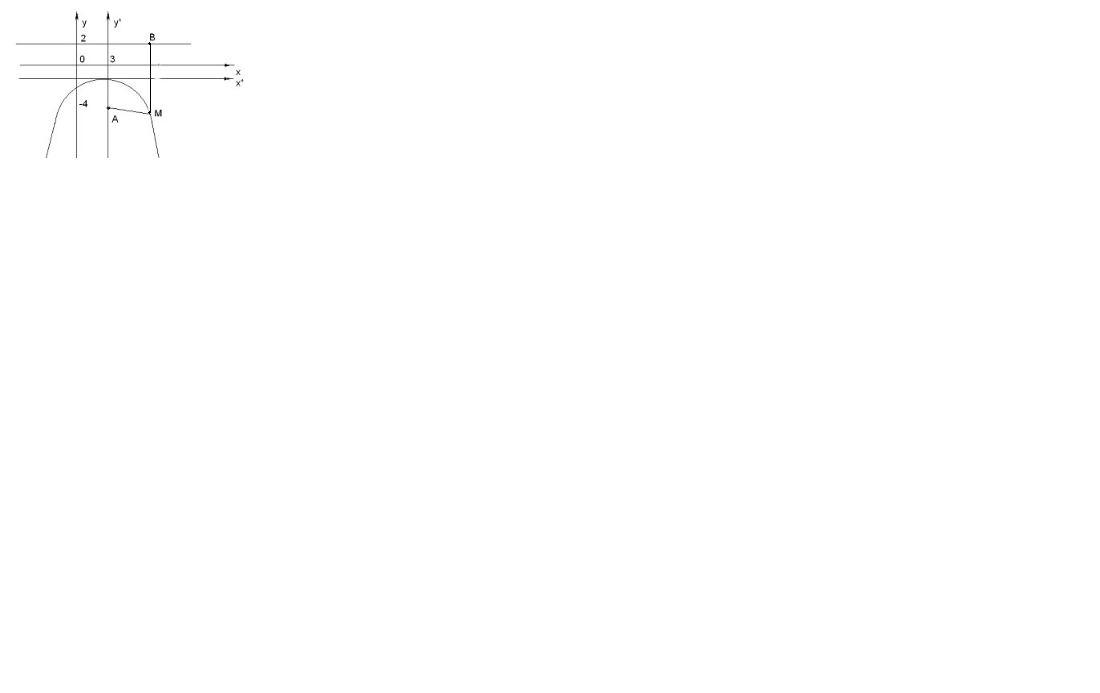
Рис.3
Полученное уравнение определяет параболу с вершиной в точке О*(3; — 1). Для приведения уравнения параболы к простейшему (каноническому) виду положим
x – 3 = X*, y+1=Y*. Тогда в системе координат Х*0*У* уравнение параболы принимает следующий вид: У*= 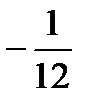 (Х*)2. В системе координат Х*0*У* строим параболу.
(Х*)2. В системе координат Х*0*У* строим параболу.
Вопросы для самопроверки
1. Дайте определение прямоугольной декартовой системы координат.
2. Напишите формулу для нахождения расстояния между двумя точками.
3. Напишите формулы для определения координат точки, делящей данный отрезок в данном отношении.
4. Напишите формулы преобразования координат: а) при параллельном переносе системы координат; б) при повороте системы координат.
5. Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через давленую точку в данном, направлении; в)проходящей через две данные точки; г) в «отрезках».
6. Как найти координаты точек пересечения двух прямых?
7. Напишите формулу для определения угла между двумя прямыми.
8. Каковы условия параллельности и перпендикулярности двух прямых?
9. Сформулируйте определение окружности.
10. Напишите уравнение окружности с центром в любой точке плоскости хОу; с центром в начале координат.
11. Дайте определение эллипса. Напишите каноническое уравнение эллипса.
12. Что называется эксцентриситетом эллипса? Как из-меняется форма эллипса с изменением эксцентриситета от 0 до 1?
13. Дайте определение гиперболы. Напишите каноническое уравнение гиперболы.
14. Напишите формулу для определения эксцентриситета гиперболы.
15. Напишите уравнения для нахождения асимптот гиперболы.
16. Сформулируйте определение параболы. Напишите каноническое уравнение параболы, симметричной относительно оси Оу.
