А) Вычисление площадей в прямоугольной системе координат.
ПРИЛОЖЕНИЯ И ПРИБЛИЖЕННЫЕ МЕТОДЫ
ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.
ПЛАН
1. Геометрические и физические приложения.
2. Приближенные методы вычисления интегралов.
Вычисление площадей плоских фигур
а) Вычисление площадей в прямоугольной системе координат.
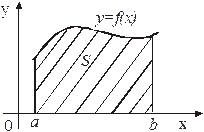 1. Если функция
1. Если функция 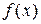 неотрицательна на
неотрицательна на
отрезке 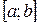 , то площадь криволинейной
, то площадь криволинейной
трапеции, ограниченной кривой 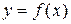
прямыми 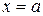 ,
, 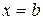 и
и 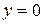 (рисунок 13),
(рисунок 13),
вычисляется по формуле:
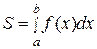 . (38) Рисунок 13
. (38) Рисунок 13
 Формула (38) справедлива на основании геометрического смысла определенного интеграла.
Формула (38) справедлива на основании геометрического смысла определенного интеграла.
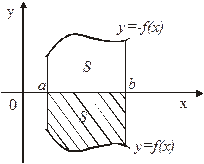
2. Если функция 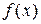 - неположительна
- неположительна
на 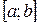 , то площадь S (рисунок 14)
, то площадь S (рисунок 14)
вычисляется по формуле:
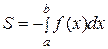 . (39)
. (39)
Действительно, отражая кривую 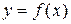
относительно оси абсцисс, получаем
кривую с уравнением 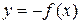 , которая Рисунок 14
, которая Рисунок 14
уже неотрицательна на отрезке 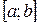 , а площадь под нею из соображений симметрии равна площади S (рисунок 14). Тогда
, а площадь под нею из соображений симметрии равна площади S (рисунок 14). Тогда 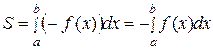 .
.
3. Если 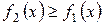 и непрерывны на отрезке
и непрерывны на отрезке 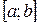 , то площадь S фигуры,
, то площадь S фигуры,
заключенной между кривыми 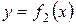 и
и 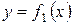 на этом отрезке
на этом отрезке
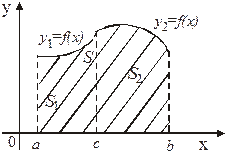
(рисунок 15)определяется формулой:
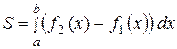 . (40)
. (40)
Рассмотрим случай, когда 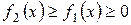
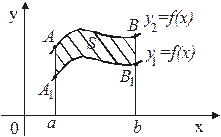
на 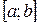 (рисунок 15). Тогда площадь S
(рисунок 15). Тогда площадь S
может быть определена как разность
соответствующих криволинейных трапеций:
Рисунок 15
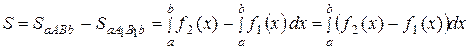 .
.
 Можно показать, что формула (40) справедлива при любых расположениях кривых у=
Можно показать, что формула (40) справедлива при любых расположениях кривых у= 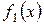 и у=
и у= 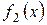 с сохранением
с сохранением
соотношения 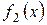 ³
³ 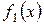 , для любых
, для любых
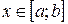 .
.
4. Если плоская фигура имеет «сложную»
форму, то прямыми, параллельными оси
Оу, ее следует разбить на части так, чтобы
можно было бы применить уже известные
формулы.
Так площадь области S, изображенной Рисунок 16
на рисунке 16 может быть найдена следующим образом:
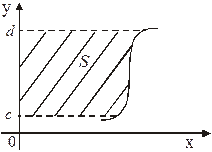
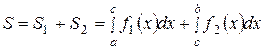 . (41)
. (41)
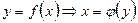 5. Если криволинейная трапеция ограничена
5. Если криволинейная трапеция ограничена
прямыми 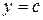 и
и 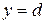 , осью Оу и непрерыв-
, осью Оу и непрерыв-
ной функцией 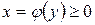 (рисунок 17), то
(рисунок 17), то
ее площадь вычисляется по формуле:
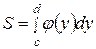 . (42)
. (42)
Рисунок 17
Пример 14. Найти площадь фигуры, ограниченной линиями: а) 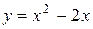 ,
, 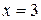 ,
, 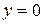 ; б)
; б) 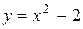 ,
, 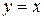 ; в)
; в) 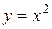 ,
, 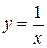 ,
, 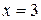 ,
, 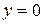 ; г)
; г) 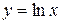 ,
, 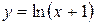 ,
, 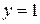 ,
, 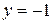 .
.
Решение. а) Заданная фигура ограничена параболой с уравнением 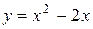 , прямой, параллельной оси ординат (
, прямой, параллельной оси ординат ( 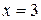 ) и осью абсцисс (
) и осью абсцисс ( 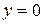 ). Как видно из рисунка 18, площадь фигуры S равна сумме площадей
). Как видно из рисунка 18, площадь фигуры S равна сумме площадей 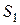 и
и 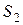 , для нахождения которых применяем формулы (39) и (38) соответственно:
, для нахождения которых применяем формулы (39) и (38) соответственно: 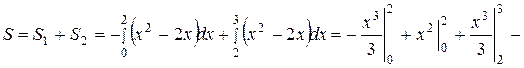
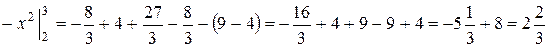 (ед2).
(ед2).
б) Фигура имеет вид, изображенный на рисунке 19. Найдем координаты точек пересечения параболы 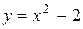 и прямой
и прямой 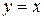 , решив систему этих уравнений
, решив систему этих уравнений 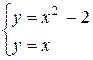 , А(-1; -1), В(2; 2). Абсциссы точек А и В пересечения этих линий задают пределы интегрирования.
, А(-1; -1), В(2; 2). Абсциссы точек А и В пересечения этих линий задают пределы интегрирования.
Так как на отрезке 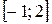 график функции
график функции 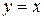 расположен «выше», чем график функции
расположен «выше», чем график функции 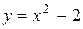 , т.е. выполняется неравенство
, т.е. выполняется неравенство 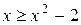 , то для нахождения площади фигуры S воспользуемся формулой (40), полагая
, то для нахождения площади фигуры S воспользуемся формулой (40), полагая 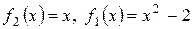 :
: 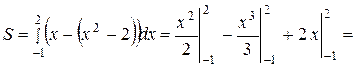
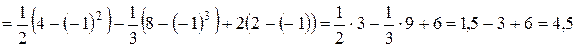 (ед2).
(ед2).
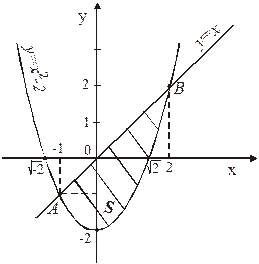
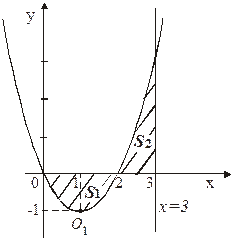
Рисунок 18 Рисунок 19
в) Фигура имеет вид изображенный на рисунке 20. Линия, ограничивающая фигуру сверху, состоит из части ОА параболы 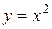 и части АВ гиперболы
и части АВ гиперболы 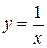 . Следовательно, площадь S найдем как сумму двух площадей:
. Следовательно, площадь S найдем как сумму двух площадей: 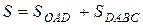 , используя формулу (41).
, используя формулу (41).
Решая систему 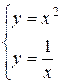 найдем координаты точки А(1; 1).
найдем координаты точки А(1; 1).
Тогда 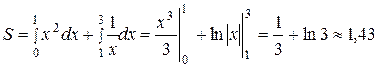 (ед2).
(ед2).
г) Искомой здесь является площадь S криволинейной трапеции АВСD (рисунок 21). В данном случае удобно использовать проецирование фигуры на ось Оу, т.е. поменять местами функцию у и аргумент х: 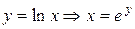 ,
, 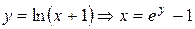 . Используя формулы (42) и (40), получаем:
. Используя формулы (42) и (40), получаем: 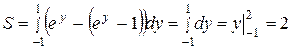 (ед2).
(ед2).
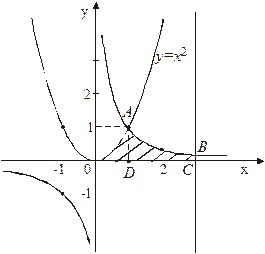
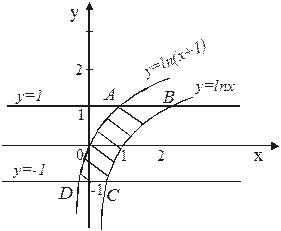
Рисунок 20 Рисунок 21
