Корневые показатели качества.
К ним относятся: степень колебательности m, степень устойчивости h и др.
Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:
Степень устойчивости h определяется как граница, правее которой корней нет, т.е.
h = min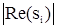 
,
где Re(si) - действительная часть корня si.
Степень колебательности m рассчитывается через угол g: m = tg g. Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g - угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:
m = min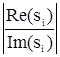 
.
Частотные показатели качества.
Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.
По АФХ определяются запасы: DA - по амплитуде, Dj - по фазе.
Запас DA определяется по точке пересечения АФХ с отрицательной действительной полуосью.
Для определения Dj строится окружность единичного радиуса с центром в начале координат. Запас Dj определяется по точке пересечения с этой окружностью.
По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке МЕ как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.
Связи между показателями качества.
Описанные выше показатели качества связаны между собой определенными соотношениями:
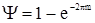; tp = 
; 
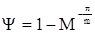; M =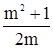 
.
Настройка регуляторов.
Типы регуляторов.
Для регулирования объектами управления, как правило, используют типовые регуляторы, названия которых соответствуют названиям типовых звеньев:
1) П-регулятор (пропорциональный регулятор)
WП(s) = K1.
Принцип действия заключается в том, что он вырабатывает управляющее воздействие на объект пропорционально величине ошибки (чем больше ошибка е, тем больше управляющее воздействие u).
2) И-регулятор (интегрирующий регулятор)
WИ(s) =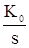 
.
Управляющее воздействие пропорционально интегралу от ошибки.
3) Д-регулятор (дифференцирующий регулятор)
WД(s) = K2 s.
Генерирует управляющее воздействие только при изменении регулируемой веричины:
u = K2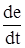 
.
На практике данные простейшие регуляторы комбинируются в регуляторы вида:
4) ПИ-регулятор (пропорционально-интегральный регулятор)
 |
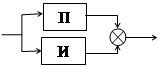WПИ(s) = K1 + .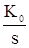
|
5) ПД-регулятор (пропорционально-дифференциальный регулятор)
 |
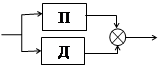WПД(s) = K1 + K2 s.
|
6) ПИД-регулятор.
WПИД(s) = K1 + 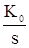+ K2 s.
Наиболее часто используется ПИД-регулятор, поскольку он сочетает в себе достоинства всех трех типовых регуляторов.