Графики тригонометрических функций

При рассмотрении графиков тригонометрических функций предполагается, что числовой аргумент представляет угол, измеренный в радианах.

Соответствие, при котором каждому действительному числу х сопоставляется синус этого числа, называют функцией синус и обозначают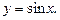

Свойства функции 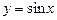приведены в табл. 4.

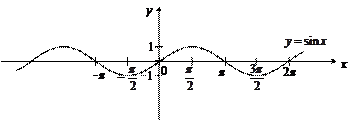Графиком функции 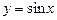является кривая, называемая синусоидой (рис. 7).

Рис. 7

Соответствие, при котором каждому действительному числу х сопоставляется косинус этого числа, называют функцией косинус и обозначают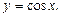

Свойства функции 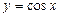приведены в табл. .

Графиком функции 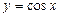является кривая, называемая косинусоидой (рис. 8).

Рис. 8

Соответствие, при котором каждому действительному числу 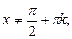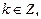сопоставляется тангенс этого числа, называется функцией тангенс и обозначается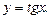

Свойства функции 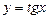приведены в табл. 4.

Графиком функции 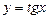является кривая, называемая тангенсоидой (рис. 9).

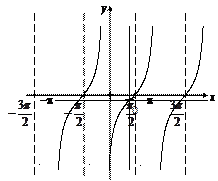
Рис. 9

Соответствие, при котором каждому действительному числу 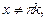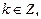сопоставляется котангенс этого числа, называется функцией котангенс и обозначается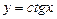

Свойства функции 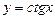приведены в табл. 4.

График функции приведен на рис. 10.

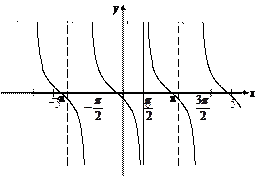
Рис. 10

Т а б л и ц а 4

Свойства функции	Функция
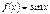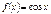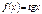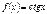1. Область определения функции	R	R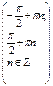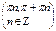
2. Область значений функции		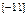	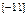R	R
3. Четность / нечетность	нечетная	четная	нечетная	нечетная
4. Наименьший положительный период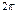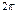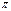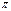
5. Координаты точек пересечения графика: с осью Ox;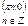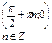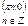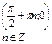
c осью Oy	(0;0)	(0;1)	(0;0)	нет
6. Промежутки возрастания функции		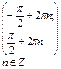		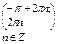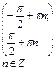нет
7.Промежутки убывания функции		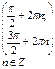	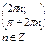нет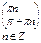
8. Экстремумы функций: точки минимума		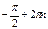	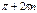нет	нет
минимум функции	-1	-1	нет	нет
точки максимума		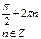	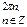нет	нет
максимум функции			нет	нет
9. Промежутки знакопостоянства функции: промежутки, на которых функция принимает положительные значения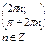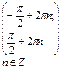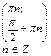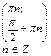
промежутки, на которых функция принимает отрицательные значения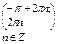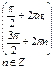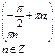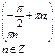

Пример 1.Найти область определения функции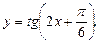

Решение. Должно выполняться 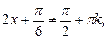х Î Z, т.е.

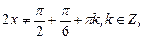
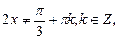
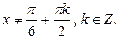
Таким образом, D(у): ,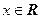

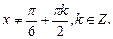
Пример 2.Найти область значений функции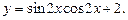

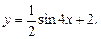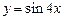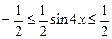Решение.Используя формулу двойного угла для синуса, получим Так как функция ограничена, то тогда и 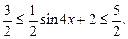Таким образом,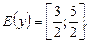

Пример 3.Выяснить, является ли функция 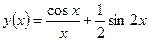четной или нечетной

Решение.Функцию можно исследовать на четность или нечетность, если область определения функции является симметричным относительно нуля множеством и выполняется одно из равенств. В данном случае D(у)= 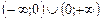- симметричное относительно нуля множество. Рассмотрим 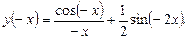В силу четности косинуса и нечетности синуса, получим

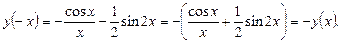
Таким образом, выполняется 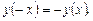Значит, данная функция является нечетной.

Пример 4.Сравнить числа и

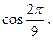
Решение.Используем свойство монотонности функции 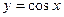на определенных промежутках. Углы 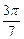и 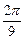принадлежат отрезку 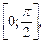на котором функция 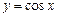убывает, и при этом 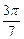> 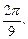Используя свойство убывающей функции, по которому большему значению аргумента соответствует меньшее значение функции, приходим к ответу: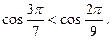

Пример 5.Найти наименьший положительный период функции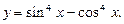

Решение.Преобразуем

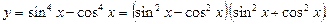
Используя формулы двойного аргумента и основное тригонометрическое тождество, получим функцию 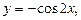график которой получается из графика функции 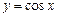с периодом 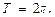Воспользуемся правилом нахождения периода Т' функции, полученной путем некоторых преобразований периодической функции 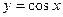с периодом : .

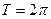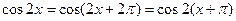Таким образом, наименьший положительный период функции 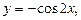а значит и функции 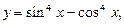равен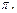

Пример 6.Найти наибольшее и наименьшее значения функции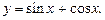

Решение. Используем формулу приведения и формулу преобразования суммы функций в произведение: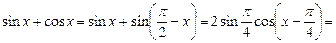

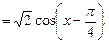
Так 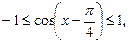то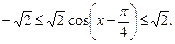

Таким образом, 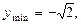а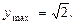

Пример 7.Построить график функции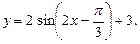

Решение. Для построения будем использовать правила преобразования графика элементарной функции 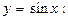параллельный перенос вдоль осей Ох и Оу, сжатие и растяжение графика функции.

Рассмотрим последовательность преобразований, позволяющих из графика функции 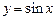получить график функции 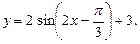Для начала преобразуем данную функцию следующим образом: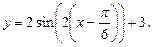

Выполним построение поэтапно.

1. График функции 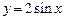может быть получен из графика 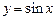путем растяжения вдоль оси Оу в 2 раза (рис. 11).

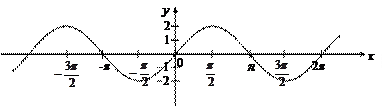Рис. 11

2. График функции 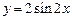может быть получен из графика функции 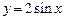путем сжатия вдоль оси Ох в 2 раза (рис. 12);

Рис. 12

3. График функции 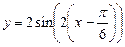может быть получен из графика 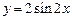путем параллельного переноса вдоль оси Ох на 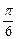единиц вправо (рис. 13);

Рис. 13

4. График 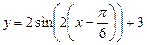получаем из графика 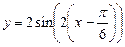путем параллельного переноса вдоль оси Оу на 3 единицы вверх (рис. 14).

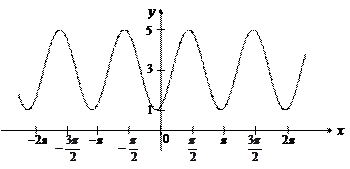
Рис. 14